Шпоры. 1. ЭВМ фон Неймана

• Название: 1. ЭВМ фон Неймана
• Анкор: Шпоры.doc
• Дата: 16.07.2018
• Размер: 0.82 Mb.
• Имя файла: Шпоры.doc
• Тип: Документы; #21572
• страница: 3 из 6

15. Триггеры. Бистабильная ячейка.


Бистабильные ячейки Триггер (от английского trigger) — спусковое устройство с набором устойчивых состояний, в которых оно может находиться сколь угодно долго.Если таких устойчивых состояний два, то такой триггер называется бистабияьным. Воздействие внешнего сигнала переводит триггер в противоположное состояние. Каждому состоянию триггера соответствуют определенные сигналы на выходах, отличающиеся высоким или низким уровнями.Если у триггера более двух устойчивых состояний, то говорят о мультистабильпых триггерах.В основе электронного триггера лежит схема бистабильной ячейки Триггер может быть реализован не только на транзисторных ключах, но и на переключателях тока. На рис. 9.2 представлена схема триггера Шмитта, реализованного на переключателях тока на основе транзисторов Т\ и Т2. Обратная связь реализуется с помощью делителя напряжения на резисторах R\ и R2. Для триггера Шмитта напряжение отпускания меньше напряжения срабатывания. В общем случае речь идет о порогах срабатывания триггера. На рис. 9.2, б показана передаточная характеристика триггера Шмитта, являющегося пороговым устройством. Характерной особенностью триггера Шмитта является гистерезисный характер его передаточной характеристики.Если амплитуда входных сигналов больше порога срабатывания, то триггер Шмитта играет роль формирователя импульсов прямоугольной формы с короткими фронтами.RS-триггер RS-триггер имеет два входа S (set — установка) и R (reset — сброс) и относится к асинхронному типу. Из анализа схем триггеров следует, что любой триггер является совокупностью нескольких определенным образом соединенных интегральных логических элементов (ИЛЭ). Для выполнения заданных функций триггер собирается из разного количества ИЛЭ, соединенных по законам булевой алгебры. Для удобства изложения будем пользоваться установленными условными обозначениями ИЛЭ. Рассматривать принципиальные электрические схемы триггеров различного назначения достаточно сложно. По способу записи информации различают асинхронные и синхронные (тактируемые) триггеры. Состояние асинхронных триггеров меняется при поступлении сигналов на входы. Состояние синхронных триггеров изменяется, прежде всего, вследствие появления тактирующих импульсов на специальных входах триггера. По окончании действия импульсов RS-триггер случайным образом установится либо g состояние Q=0 или Q= 1. Такая комбинация R = S=\ приводит к неопределенному состоянию RS-триггера и поэтому одновременная подача импульсов на оба входа не допускается. Максимальная частота переключения триггера определяется минимально доступным временным интервалом между двумя сигналами, которые поступают на входы триггера.RST-триггер Триггеры, у которых состояние меняется только путем поступления тактовых импульсов, называют синхронными триггерами. К ним относятся RST-триггер, имеющий времязадающий вход С (clock). В промежутках между тактовыми импульсами изменения сигналов на входах не вызывают переключения триггера.

Т-триггер Счетный Т-триггер предназначен для изменения своего состояния на противоположное

каждый раз, когда на единственный вход поступает управляющий импульс (С= 1). Другими словами, он способен считать импульсы на входе. В основе конструкции Т-триггера лежат два RST-триггера, соединенные с инверторомВ результате действия каждого управляющего импульса Т-триггер переключается в противоположное состояние с задержкой. Задержка равна длительности импульса.Характеристическое уравнение Т-триггера имеет вид: O"+i=CQ"+CC>", где CQ" — значение во время тактового импульса, a CQ" — по его окончании.JK-триггер JK-триггеры (jump — переброс, keep — держать) являются универсальными и относятся к категории синхронных. Другими словами, выходные уровни устанавливаются только при поступлении тактовых импульсов. В основе JK-триггера лежит структура Т-триггера, входы которого связаны с выходами перекрестными обратными связями. JK-триггер имеет два информационных входа: J и К, а также тактовый вход С

17. Микропроцессоры и устройства на их основе.

Микропроцессор является самостоятельной или составной частью вычислительного устройства, осуществляющей обработку информации и управление этим процессом, которая выполнена в виде интегральной схемы.

Микропроцессор наряду с запоминающими устройствами, интерфейсом является основой ряда вычислительных устройств, микро-ЭВМ, персональных компьютеров.

Структурная схема микропроцессора включается в себя арифметико-логическое устройство (АЛУ), устройство управления (УУ), регистры (Р) и устройство ввода-вывода информации (УВВ) или интерфейс. Микропроцессор управляется сигналами трех видов: 1.адресными, передающимися по адресным шинам (АШ) 2.информационными, передающимися по разрядным шинам (РШ) 3.сигналами, управляющими микропроцессором соответственно через шины управления (ШУ).

Шины представляют собой группу линий связи, число которых определяется, прежде всего, разрядностью обрабатываемого информационного сигнала. Шины – двунаправленные, позволяющие передавать информацию в обоих направлениях. Иногда шины объединяют в одну или две.

АЛУ предназначено для выполнения всех операций вычислительного процесса. В АЛУ осуществляется обработка инф. по кодам программы, совершаются арифметические и логические операции над числами и адресами, представленными в двоичном коде.

УУ управляет работой АЛУ и всех других элементов микропроцессора. Уз программы, хранящейся в ПЗУ в УУ, поступают команды в виде двоичных сигналов, стимулирующие выполнение команды. УУ распределяет так же очередность выполнения команд во времени.

Регистры микропроцессора представляют собой ячейки памяти, служащие для сверхоперативного хранения только текущей информации (СОЗУ).

Указатель стека предназначен для взаимодействия с внешним запоминающимся устройством с произвольной выборкой, в котором хранятся промежуточные данные. Стек это динамическая структура, работающая по принципу “последний пришел – первый ушел”.

В состав микропроцессора в качестве вспомогательного устройства включается таймер Т. Его работа определяет во времени порядок работы всех разрядных, адресных и управляющих сигналов, а также синхронизирует работу УУ.

Микропроцессоры и устройства на его основе в современной микроэлектронике являются наиболее значимыми и распространенными изделиями. Однако применение микропроцессора без системной поддержки ряда других устройств употребляется весьма ограничено.

Микроконтроллер представляет собой микропроцессорную систему, предназначенную для управления, которая выполнена на основе одной или нескольких микропроцессорных БИС и способна к программированию. Для микроконтроллеров характерны малая потребляемая мощность, расширенные возможности работы с памятью, низкая стоимость.

Микро-ЭВМ представляет собой конструктивно завершенное вычислительное устройство, реализованное на базе микропроцессорного компонента СБИС и оформленное в виде автономного устройства с источником питания, интерфейсом, устройством отображения информации и комплектом программного обеспечения. Микро-ЭВМ получили название персональных компьютеров (ПК).

На базе микропроцессоров создаются мультипроцессорные системы, в которых используются более одного микропроцессора и которые предназначены для обработки информации, в том числе и для параллельной обработки.

Суперкомпьютер – вычислительное устройство общего назначения, выполняющее большие вычислительные задачи с числом операций порядка триллиона.

18. Начала наноэлектроники.

Под наноэлектроникой понимают направление электроники, в котором изучаются физические явления и процессы взаимодействия электронов с электромагнитными полями, а так же разработка нанотехнологии создания приборов и устройств, в которых дано взаимодействие используется для передачи, обработки и хранения информации.

Под нанотехнологией будем понимать совокупность способов и приемов создания элементов и приборов нанометровых размеров, в том числе из отдельных молекул и атомов.

Исключительно малая инерционность электронов позволяет эффективно использовать взаимодействие электронов с микрополями внутри атома, молекулы или кристаллической решетки для создания приборов и устройств нового поколения, отличающихся высокой производительностью, ничтожным потреблением энергии, сверхминиатюрными размерами.

Наноэлектроника является логическим развитием микроэлектроники. Твердотельные информационные приборы уменьшились от микро- (м) до нанометрового (м) размера.

Если в микроэлектронных приборах поведение электрона определялось поведением элементарной частицы, имеющей массу и заряд, то в наноэлектронных приборах поведение электрона определяется его волновыми свойствами.

Де-бройлевская длина волны электрона равна

или , где P –импульс, m-масса электрона, V-скорость его движения, h-постоянная Планка.

Импульс электрона P связан с ускоряющим напряжением соотношением , где E-энергия электрона. Для определения длины волны электрона удобно пользоваться практической формулой , где V-ускоряющее напряжение.

Движение электрона как электронов и уравнением Дирака для релятивистских волны описывается уравнением Шредингера для нерелятивистских. В наноэлектронике обычно используются нерелятивистские электроны. Для электрона массой , движущегося под действием силы, порождаемой потенциалом V(x, y, z, t), уравнение Шредингера имеет вид:

или

, где -волновая функция, -оператор Лапласса, H-оператор Гамильтона, E-полная энергия электрона, r-функция положения электрона в пространстве. Движение электрона в свободном пространстве V(r)=C описывается уравнением

=

19. Закон сохранения электрического заряда. Закон Кулона. Основные характеристики электростатического поля – напряженность и потенциал.

В замкнутой системе, в которую не входят извне электрические заряды и из которой не выходят заряды, при любых взаимодействиях тел алгебраическая сумма электрических зарядов всех тел остается постоянной:

q1 + q2 +...+ qn = const

Все тела в природе способны электризоваться, т.е. приобретать электрический заряд. Наличие электрического заряда проявляется в том, что заряженное тело взаимодействует с другими заряженными телами. Имеются 2 вида электрических зарядов, условно называемых положительными и отрицательными. Заряды одного знака отталкиваются, заряды разных знаков притягиваются. Электрический заряд является свойством некоторых элементарных частиц, например электрон имеет отрицательный заряд –e, протон – положительный заряд +e, нейтрон – заряд равный нулю. Заряд элементарных частиц одинаковый по величине и называется элементарным зарядом. Закон(закон взаимодействия точечных зарядов): Сила взаимодействия двух неподвижных точечных зарядов пропорциональна величине каждого из зарядов и обратно пропорциональна квадрату расстояния между ними. Направление силы совпадает с направлением прямой соединяющей заряды.

, k – коэффициент пропорциональности, предполагается положительным, - единичный вектор, имеющий направление от одного заряда к другому.

Напряженность электростатического поля.

Всякий заряд изменяет свойства окружающего его пространства – создает в нем электрическое поле. Это поле проявляется в том, что помещенный в какую-либо его точку электрический заряд испытывает воздействие силы. Взаимодействие между зарядами осуществляется через электрическое поле. Будем вносить пробные заряды в поле неподвижного точечного заряда и измеряя силы, действующие на пробный заряд было установлено что отношение для всех пробных зарядов остается постоянным и зависит только от q и r, определяющих поле в данной точке.

Величину , характеризующую электрическое поле называют напряженностью электрического поля в данной точке пространства.

Направление вектора напряженности E – вдоль радиальной прямой, проходящей через заряд и данную точку поля, от заряда, если он положителен, и к заряду, если он отрицателен.

Потенциал электростатического поля. Поле консервативной силы может быть описано не только векторной функцией, но эквивалентное описание этого поля можно получить, определив в каждой его точке подходящую скалярную величину. Для электростатического поля такой величиной является потенциал электростатического поля, определяемый как отношение потенциальной энергии пробного заряда q к величине этого заряда,

фи = Wп/q, откуда следует, что потенциал численно равен потенциальной энергии, которой обладает в данной точке поля единичный положительный заряд. (1 В).

Потенциал электростатического поля.

Внося в данную точку поля различные пробные заряды q1,q1,…qn мы будем, соответственно, изменять потенциальную энергию, т.е. получим различные W1,W2,…Wn. Но отношение потенциальной энергии к заряду остается величиной постоянной. Следовательно для характеристики поля можем использовать это отношение. Обычно оно обозначается буквой фи и называется потенциалом поля в данной точке .

Потенциал является энергетической характеристикой поля. Он численно равен работе, которую надо затратить против сил электрического поля при перенесении единичного положительного точечного заряда из бесконечности в данную точку поля. Единица измерения потенциала - вольт.



Когда поле образовано несколькими произвольно расположенными зарядами q1,q2,…,qn, потенциал его в данной точке равен алгебраической сумме потенциалов фи1,фи2,…,фиn , создаваемых каждым зарядом в отдельности.

\

20. Поток вектора напряженности. Теорема Остроградского – Гаусса для электростатического для в вакууме.

Поток вектора.

Число линий вектора E, пронизывающих некоторую поверхность S, называется потоком вектора напряженности N_E.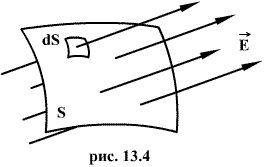



Для вычисления потока вектора E необходимо разбить площадь S на элементарные площадки dS, в пределах которых поле будет однородным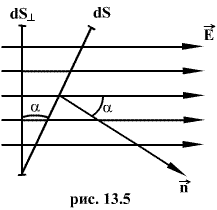



Поток напряженности через такую элементарную площадку будет равен по определению



где 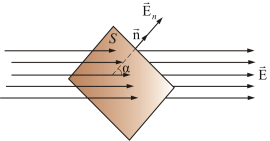- угол между силовой линией и нормалью к площадке dS; - проекция площадки dS на плоскость, перпендикулярную силовым линиям. Тогда поток напряженности поля через всю поверхность площадки S будет равен







Полное число силовых линий, проходящих через поверхность S называется потоком вектора напряженности Ф_Е через эту поверхность.

Величина - поток вектора через поверхность. Поток вектора – это алгебраическая величина, знак которой зависит от выбор направления нормали к элементарной площадке, на которые разбивается поверхность S.

Теорема Остроградского-Гаусса

Полный поток вектора напряженности электростатического поля через замкнутую поверхность произвольной формы численно равен алгебраической сумме свободных электрических зарядов, заключенных внутри этой поверхности. Это положение называется теоремой Остроградского - Гаусса. С помощью этой теоремы можно определить напряженность полей, создаваемых заряженными телами различной формы.



В случае, если замкнутая поверхность любой формы охватывает заряд (рис. 2), то при пересечении любой линии напряженности с поверхностью она то входит в нее, то выходит из нее. При вычислении потока нечетное число пересечений в конечном счете сводится к одному пересечению, так как поток полагается положительным, если линии напряженности выходят из поверхности, и отрицательным для линий, которые входят в поверхность.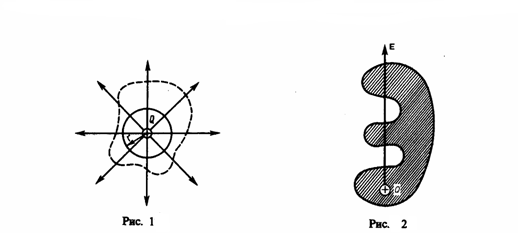



Если замкнутая поверхность не охватывает заряда, то поток сквозь нее равен нулю, так как число линий напряженности, которые входят в поверхность, равно числу линий напряженности, которые выходят из нее.

Значит, для поверхности произвольной формы, если она замкнута и заключает в себя точечный заряд Q, поток вектора Е будет равен Q/ε₀, т. е. (1)

Знак потока совпадает со знаком заряда Q. Исследуем общий случай произвольной поверхности, окружающей n зарядов. Используя с принцип суперпозиции, напряженность Е поля, которая создавается всеми зарядами, равна сумме напряженностей E_i полей, которые создаваются каждым зарядом в отдельности. Поэтому

Согласно (1), каждый из интегралов, который стоит под знаком суммы, равен Q_i/ε₀. Значит, (2)

Формула (2) выражает теорему Гаусса для электростатического поля в вакууме: поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на ε₀.

23. Работа по перемещению заряда в электростатическом поле. Энергия электростатического поля. Объемная плотность энергии.

Элементарная работа, совершаемая силой F при перемещении точечного электрического заряда из одной точки электростатического поля в другую на отрезке пути , по определению равна

где - угол между вектором силы F и направлением движения . Если работа совершается внешними силами, то dA=0. Интегрируя последнее выражение, получим, что работа против сил поля при перемещении пробного заряда из точки “а” в точку “b” будет равна



где - кулоновская сила, действующая на пробный заряд в каждой точке поля с напряженностью Е. Тогда работа

Энергия электрического поля.

Опыт показывает, что заряженный конденсатор содержит запас энергии.

Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор.

Процесс зарядки конденсатора можно представить как последовательный перенос достаточно малых порций заряда Δq > 0 с одной обкладки на другую. При этом одна обкладка постепенно заряжается положительным зарядом, а другая – отрицательным. Поскольку каждая порция переносится в условиях, когда на обкладках уже имеется некоторый заряд q, а между ними существует некоторая разность потенциалов при переносе каждой порции Δq внешние силы должны совершить работу . Энергия W_е конденсатора емкости C, заряженного зарядом Q, может быть найдена путем интегрирования этого выражения в пределах от 0 до Q: .

Формулу, выражающую энергию заряженного конденсатора, можно переписать в другой эквивалентной форме, если воспользоваться соотношением Q = CU.

Напряженность однородного поля в плоском конденсаторе равна E = U/d, а его емкость Поэтому

где V = Sd – объем пространства между обкладками, занятый электрическим полем.

Объемная плотность энергии.

Это физическая величина, численно равная отношению потенциальной энергии поля, заключенной в элементе объема, к этому объему. Для однородного поля объемная плотность энергии равна . Для плоского конденсатора, объем которого Sd, где S - площадь пластин, d - расстояние между пластинами, имеем

С учетом, что и :

.

21. Электрическое поле в веществе. Свободные и связанные заряды. Проводники и диэлектрики. Типы диэлектриков.

Любая среда ослабляет напряженность электрического поля. Электрические характеристики среды определяются подвижностью заряженных частиц в ней вещества: проводники, полупроводники, диэлектрики.

Характерным свойством проводников является наличие свободных электрических зарядов. В металлах носителями свободных зарядов являются электроны. При образовании металла из нейтральных атомов атомы начинают взаимодействовать друг с другом. Благодаря этому взаимодействию электроны внешних оболочек атомов полностью утрачивают связи со «своими» атомами и становятся «собственностью» всего проводника в целом. В результате положительно заряженные ионы оказываются окруженными отрицательно заряженным «газом», образованным коллективизированными электронами. Этот газ заполняет промежутки между ионами и стягивает их кулоновскими силами. Свободные электроны участвуют в тепловом движении подобно молекулам газа и могут перемещаться по металлу в любом направлении.

Диэлектрики - вещества, содержащие только связанные заряды

Если внести диэлектрик в электрическое поле, то это поле и сам диэлектрик претерпевают существенные изменения. Заряды в диэлектриках могут смещаться из положения равновесия на малые расстояния, порядка атомных. Внешнее электрическое поле стремится сдвинуть положительные заряды в направлении поля, а отрицательные – в противоположном. В результате весь диэлектрик приобретает макроскопический электрический дипольный момент. Этот процесс называется поляризацией

Свободные и связанные заряды.

При рассмотрении электростатического поля, в случае наличия в нем диэлектриков, нужно различать два рода электрических зарядов: свободные и связанные. Под свободными зарядами мы будем понимать, во-первых, все электрические заряды, которые под влиянием электрического поля могут перемещаться на макроскопические расстояния (электроны в металлах и вакууме, ионы в газах и электролитах и т. п.), и, во-вторых, заряды, нанесенные извне на поверхность диэлектриков и нарушающие их нейтральность). Заряды же, входящие в состав нейтральных молекул диэлектриков, равно как и ионы, закрепленные в твердых диэлектриках вблизи определенных положений равновесия, мы будем называть зарядами связанными.

Проводники и диэлектрики

Основная особенность проводников – наличие свободных зарядов (электронов), которые участвуют в тепловом движении и могут перемещаться по всему объему проводника. Типичные проводники – металлы.

По электрическим свойствам тела можно разделить на проводники и диэлектрики. Проводниками называют тела, через которые электрические заряды могут переходить от заряженного тела к незаряженному. Способность проводников пропускать через себя электрические заряды объясняется наличием в них свободных носителей заряда. Примерами проводников могут служить металлические тела в твердом и жидком состоянии, жидкие растворы электролитов.

Диэлектриками, или изоляторами, называются такие тела, через которые электрические заряды не могут переходить от заряженного тела -к незаряженному. К диэлектрикам, например, относятся воздух и стекло, плексиглас и эбонит, сухое дерево и бумага.

Типы диэлектриков.

Диэлектриками называются вещества, которые в обычных условиях практически не проводят электрический ток, их удельное сопротивление в раз больше, чем у металлов. Согласно представлениям классической физики, в диэлектриках, в отличие от проводников, нет свободных носителей заряда, которые могли бы под действием электрического поля создавать ток проводимости. К диэлектрикам относятся все газы; некоторые жидкости (дистиллированная вода, масла, бензол); твердые тела (стекло, фарфор, слюда).

Диэлектрики, как и любые вещества, состоят из атомов и молекул. В целом молекулы нейтральны, тем не менее, они взаимодействуют с электрическим полем. Например, в случае, когда симметрия молекулы отлична от сферической, ее можно представить в виде электрического диполя. Электрический дипольный момент молекулы p_i=ql , где q - суммарный заряд ядер или электронов; l - вектор, представляющий собой плечо эквивалентного диполя.

Молекулы, обладающие электрическим дипольным моментом, называют полярными. Полярным диэлектриком является вода; следующие вещества: CO; N2O; S2O; NH; HCl также имеют в своем составе полярные молекулы. В объеме вещества дипольные моменты молекул распределены по разным направлениям хаотическим образом, так что их сумма равна нулю.

Молекулы, у которых положения эквивалентного положительного и эквивалентного отрицательного заряда совпадают и, следовательно, дипольный момент каждой молекулы равен нулю (p_i=0), называют неполярными. Такие вещества, как H₂, N₂, O2, CO2 состоят из неполярных молекул.


22. Проводники в электрическом поле. Электроемкость уединенного проводника. Взаимная емкость двух проводников. Конденсаторы.

Проводниками называют вещества, в которых есть свободные носители зарядов. Например, в металлах ими являются свободные электроны.  В отсутствие поля свободные электроны совершающие тепловые движения. Под действием электрического поля свободные электроны металлической пластины начинает перемещаться против линии напряженности электрического поля.

24. Закон Ома в интегральной форме.
Закон Ома для участка электрической цепи имеет вид: U = RI
где:U — напряжение или разность потенциалов,
I — сила тока,R — сопротивление.
Закон Ома также применяется ко всей цепи, но в несколько изменённой форме:I=E/(R+r), где:e — ЭДС цепи,I — сила тока в цепи,R — сопротивление всех элементов цепи,
r — внутреннее сопротивление источника питания.
Закон Ома в дифференциальной форме
Сопротивление R зависит как от материала, по которому течёт ток, так и от геометрических размеров проводника. Полезно переписать закон Ома в так называемой дифференциальной форме, в которой зависимость от геометрических размеров исчезает, и тогда закон Ома описывает исключительно электропроводящие свойства материала. Для изотропных материалов имеем:
j=σ*E
где j- вектор плотности тока, σ — удельная проводимость, E — вектор напряжённости электрического поля.
Все величины, входящие в это уравнение, являются функциями координат и, в общем случае, времени. Если материал анизотропен, то направления векторов плотности тока и напряжённости могут не совпадать. В этом случае удельная проводимость является тензором ранга (1, 1).
Электродвижущая сила (ЭДС) — физическая величина, характеризующая работу сторонних (непотенциальных) сил в источниках постоянного или переменного тока. В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительного заряда вдоль контура.

ЭДС можно выразить через напряжённость электрического поля сторонних сил (E_ex). В замкнутом контуре (L) тогда ЭДС будет равна:

,

где dl — элемент длины контура.

ЭДС так же, как и напряжение, измеряется в вольтах. Можно говорить об электродвижущей силе на любом участке цепи. Это удельная работа сторонних сил не во всем контуре, а только на данном участке

Электри́ческое сопротивле́ние — физическая величина, характеризующая свойства проводника препятствовать прохождению электрического тока и равная отношению напряжения на концах проводника к силе тока, протекающего по нему^[1]. Сопротивлением (резистором) также называют радиодеталь, предназначенную для введения в электрические цепи активного сопротивления.

Сопротивление (часто обозначается буквой R или r) считается, в определённых пределах, постоянной величиной для данного проводника; её можно рассчитать как



Где R — сопротивление; U — разность электрических потенциалов на концах проводника;

I — сила тока, протекающего между концами проводника под действием разности потенциалов.

Зако́н Видема́на — Фра́нца — это физический закон, утверждающий, что для металлов отношение коэффициента теплопроводности (либо тензора теплопроводности) K к удельной электрической проводимости (либо тензору проводимости) σ пропорционально температуре:

. L — постоянная, одинаковая для всех металлов, называется числом Лоренца.

В 1853 г было установлено, что для различных металлов при одинаковой температуре отношение K / σ практически не изменяется.

Взаимная связь электрической проводимости и теплопроводности объясняется тем, что оба эти свойства металлов в основном обусловлены движением свободных электронов.

Коэффициент теплопроводности увеличивается пропорционально средней скорости частиц, так как ускоряется перенос энергии. Электропроводность, наоборот, падает, потому что соударения при большой скорости частиц значительно затрудняют перенос энергии .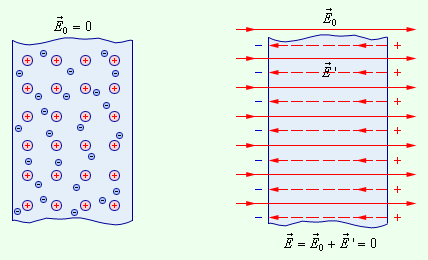

Левая часть пластины заряжается отрицательно, а правая положительно. В этом состоит явление электростатической индукции. Электроны перемещаются за ничтожно малое время до тех пор пока напряженность результирующего поля внутри пластины не станет равным нулю. Электростатическое поле внутри проводника равно 0, так как E_внутр и E_внешн равны по модулю, но противоположно направлены (E = 0).

Носители заряда в проводнике способны перемещаться под действием сколь угодно малой силы. Поэтому для равновесия зарядов на проводнике необходимо выполнение следующих условий:

- напряженность поля всюду внутри проводника должна быть равна нулю ; (потенциал внутри проводника должен быть постоянным)

- напряженность поля на поверхности проводника должна быть в каждой точке направлена по нормали к поверхности .

Следовательно в случае равновесия зарядов поверхность проводника будет эквипотенциальной. Если проводящему телу сообщить заряд q, то он распределиться так, чтобы соблюдались условия равновесия. Пусть имеет произвольную замкнутую поверхность полностью заключенную внутри тела. При равновесии зарядов поле в каждой точке отсутствует, поэтому поток электрического смещения равен нулю

По теореме Гаусса сумма зарядов внутри поверхности тоже будет равна нулю. Следовательно при равновесии зарядов ни в каком месте проводника не может быть избытка зарядов, они распределяются равномерно по поверхности с некоторой плотностью σ.

Электроемкость.

Пусть имеем уединенный проводник, тогда его потенциал пропорционален находящемуся на нем заряду. Действительно увеличение в несколько раз заряда приводит к увеличению в то же число раз напряженности поля в каждой точке окружающего проводник пространства. Соответственно в такое же число раз возрастает и работа переноса единичного заряда из бесконечности на поверхность проводника, т.е. потенциал проводника. Т.о. для уединенного проводника .

Коэффициент пропорциональности С называется электроемкостью проводника (или емкостью) . Емкость величина численно равная заряду, сообщение которого изменяет потенциал проводника на единицу. Единица емкости – Фарада (Ф) 1Ф = 1Кл/1В (Вольт).

Взаимная емкость проводников.

Взаимная емкость двух проводников зависит от их формы, размеров и взаимного расположения, а также от диэлектрических свойств окружающей среды.

Уединенные проводники обладают небольшой емкостью. Даже шар размером с Землю обладает емкостью только 700 мкФ. Однако на практике бывает потребность в устройствах, которые при небольшом относительно окружающих тел потенциале накапливали бы на себе (конденсировали) большие по величине заряды. Такие устройства называются конденсаторами и в их основу положен тот факт, что электроемкость проводников возрастает при приближении к ним других тел.

Это вызвано тем, что под действием поля, создаваемого заряженным проводником, на поднесенном к нему теле возникают индуцированные заряды. Заряды противоположные по знаку заряду проводника q располагаются ближе к проводнику и оказывают влияние на проводник. А именно его потенциал уменьшается, а следовательно емкость возрастает.

Конденсаторы делают в виде двух проводников, помещенных близко друг к другу, образующие конденсатор проводники называются его обкладками. Чтобы внешние тела не оказывали влияние на емкость конденсатора, их делают такими (по форме и расположению друг относительно друга), чтобы поле, создаваемое зарядами было сосредоточено внутри конденсатора.

Это могут быть две пластинки, две концентрические сферы, два коаксиальных цилиндра. Следовательно, сущ. плоские, сферические и цилиндрические конденсаторы. Так как поле сосредоточено внутри конденсатора, линии напряженности начинаются на одной обкладке и заканчиваются на другой. И след. Сторонние заряды, возникающие на обкладках, имеют одинаковую величину и противоположны по знаку.

Основной характеристикой конденсатора является его емкость, под которой понимают величину, пропорциональную заряду и обратно пропорциональную разности потенциалов между обкладками .

Разность потенциалов называют напряжением между соответствующими точками и обозначают буквой U (напряжение между обкладками). Тогда можно переписать формулу.



Емкость конденсаторов измеряется в тех же единицах, что и емкость уединенного проводника. Величина емкости зависит от геометрии конденсатора (форме, размеров, расстояния между обкладками), а также диэлетрическими свойствами среды, заполняющими пространство между обкладками.


25. Работа и мощность тока. Закон Джоуля Ленца

Прохождение электрического тока по проводнику представляет собой процесс упорядоченного движения зарядов в электрическом поле, существующем в проводнике. При этом силы электрического поля, действующие на заряды, совершают работу. Назовем эту работу «работой тока» (Aэл.) и рассчитаем ее на участке цепи 1-2, содержащем сопротивление R
Из электростатики известно, что: Aэл. = q*(f1 — f2).
q = I*t; U = I*R; U = f1 — f2

где:

t — время прохождения тока,

q — заряд, прошедший от точки с потенциалом f1 до точки с потенциалом f2.
Следовательно, работу тока можно вычислить с помощью следующего соотношения:

Aэл. = I*U*t = (I^2)*R*t = (U^2)*t/R

Мощностью (Nэл.) называется работа, совершаемая током за единицу времени:

Nэл. = Aэл./t

Следовательно,

Nэл. = I*U = (I^2)*R = (U^2)/R

Мощность электрического тока на опыте определяется с помощью амперметра и вольтметра или специального прибора — ваттметра.
Закон Джоуля-Ленца

Если по активному сопротивлению (проводнику) течет постоянный ток, то работа тока на этом участке идет на преобразование электрической энергии во внутреннюю. Увеличение внутренней энергии проводника приводит к повышению его температуры (проводник нагревается).

По закону сохранения энергии количество теплоты (Q), выделяющееся в проводнике при прохождении электрического тока, равно работе тока: Q = Aэл.

Следовательно,

Q = I*U*t = (I^2)*R*t = (U^2)*t/R

Эта формула есть закон Джоуля-Ленца для однородного участка цепи.

Закон Джоуля–Ленца в интегральной форме:

26. Магни́тное по́ле 

— силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения, магнитная составляющая электромагнитного поля. Магнитное поле может создаваться током заряженных частиц и/или магнитными моментами электронов в атомах.

Единицы измерения

Величина B в системе единиц СИ измеряется в теслах.Векторное поле H измеряется в амперах на метр (А/м) в системе СИ.

Магни́тная инду́кция  — векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой магнитное поле действует на заряд q, движущийся со скоростью .

Также магнитная индукция может быть определена как отношение максимального механического момента сил, действующих на рамку с током, помещенную в однородное поле, к произведению силы тока в рамке на её площадь.

Напряжённость магни́тного по́ля — (стандартное обозначение Н) это векторная физическая величина, равная разности вектора магнитной индукции B и вектора намагниченности M.

В СИ: , где μ0 -  магнитная постоянная

Намагни́ченность — это векторная физическая величина, характеризующая магнитное состояние макроскопического физического тела.

Здесь, M — вектор намагниченности; m вектор магнитного момента; V — объём.

В вакууме (или в отсутствии среды, способной к магнитной поляризации, а также в случаях, когда последняя пренебрежима) напряженность магнитного поля совпадает с вектором магнитной индукции.

В магнетиках (магнитных средах) напряженность магнитного поля имеет физический смысл «внешнего» поля, то есть совпадает (быть может, в зависимости от принятых единиц измерения, с точностью до постоянного коэффициента, как например в системе СИ, что общего смысла не меняет) с таким вектором магнитной индукции, какой «был бы, если магнетика не было».

Вихревой характер магнитного поля означает просто замкнутость линий магнитной индукции - т.е. пробные магнитные стрелки будут с разных сторон диаметра окружности, охватывающей провод, будут ориентированы противоположно. Вот и все.

27. закон био-савара лапласа и его применение к расчёту магнитного поля прямолинейного проводникас током и витка с током.

Закон Био — Савара — Лапласа для проводника с током I, элемент dl которого создает в некоторой точке А (рис. 164) индукцию поля dB, записывается в виде

(110.1)

где dl — вектор, по модулю равный длине dl элемента проводника и совпадающий по направлению с током, r—радиус-вектор, проведанный из элемента dl проводника в точку А поля, r — модуль радиуса-вектора r. Направление dB перпендикулярно dl и r, т. е. перпендикулярно плоскости, в которой они лежат, и совпадает с касательной к линии магнитной индукции. Это направление может быть найдено по правилу нахождения линий магнитной индукции (правилу правого винта): направление вращения головки винта дает направление dB, если поступательное движение винта соответствует направлению тока в элементе.

Модуль вектора dB определяется выражением

(110.2)

где a — угол между векторами dl и r.

Для магнитного поля, как и для электрического, справедлив принцип суперпозиции: магнитная индукция результирующего поля, создаваемого несколькими токами или движущимися зарядами, равна векторной сумме магнитных индукций складываемых полей, создаваемых каждым током или движущимся зарядом в отдельности:

(110.3)

Расчет характеристик магнитного поля (В и Н) по приведенным формулам в общем случае сложен. Однако если распределение тока имеет определенную сим­метрию, то применение закона Био — Савара — Лапласа совместно с принципом суперпозиции позволяет просто рассчитать конкретные поля. Рассмотрим два примера.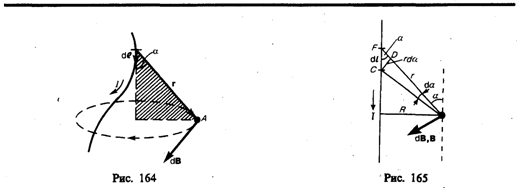

1. Магнитное поле прямого тока — тока, текущего по тонкому прямому проводу бесконечной длины (рис. 165). В произвольной точке А, удаленной от оси проводника на расстояние R, векторы dB от всех элементов тока имеют одинаковое направление, перпендикулярное плоскости чертежа («к вам»). Поэтому сложение векторов dB можно заменить сложением их модулей. В качестве постоянной интегрирования выберем угол a (угол между векторами dl и r), выразив через него все остальные величины. Из рис. 165 следует, что



(радиус дуги CD вследствие малости dl равен r, и угол FDC по этой же причине можно считать прямым). Подставив эти выражения в (110.2), получим, что магнитная индукция, создаваемая одним элементом проводника, равна

(110.4)

Так как угол a для всех элементов прямого тока изменяется в пределах от 0 до p, то, согласно (110.3) и (110.4),



Следовательно, магнитная индукция поля прямого тока

(110.5)

2. Магнитное поле в центре кругового проводника с током (рис. 166). Как следует из рисунка, все элементы кругового проводника с током создают в центре магнитные поля одинакового направления — вдоль нормали от витка. Поэтому сложение векторов dB можно заменить сложением их модулей. Так как все элементы проводника перпендикулярны радиусу-вектору (sina =1) и расстояние всех элементов проводника до центра кругового тока одинаково и равно R, то, согласно (110.2),

Тогда



Следовательно, магнитная индукция поля в центре кругового проводника с током

28. Сила Лоренца. Движение заряженных частиц в магнитном поле. Закон Ампера.

Силы, с которыми магнитное поле действует на проводник с током, являются силами, действующими на движущиеся заряды (электроны или ионы), которые и составляют ток. Эти силы наз-ют силами Лоренца. Сила Лоренца, действ-ая на электрон е, движ-ся в магнитном поле, перпендикулярна к скорости электрона v и к магнитной индукции В. Направление этой силы может быть определено по правилу левой руки.

ЛЕВОЙ РУКИ ПРАВИЛО: определяет направление силы, к-рая действует на находящийся в магн. поле проводник с током. Если ладонь левой руки расположить так, чтобы вытянутые пальцы были направлены по току, а силовые линии магн. поля входили в ладонь, то отставленный большой палец укажет направление силы, действующей на проводник.



Буравчика правило: если буравчик ввинчивать по направлению тока (I), то направление вращения рукоятки буравчика совпадает с направлением магнитного поля (Н), возбуждаемого этим током.

при движении частицы в любом стационарном магнитном поле кинетическая энергия и модуль скорости частицы сохраняются – изменяется только направление вектора скорости частицы. Закон Ампера: что сила , с которой магнитное поле действует на элемент проводника с током, находящегося в магнитном поле, прямо пропорциональна силе тока I в проводнике и векторному произведению элемента длины проводника на магнитную индукцию :

при движении частицы в любом стационарном магнитном поле кинетическая энергия и модуль скорости частицы сохраняются – изменяется только направление вектора скорости частицы