|
|
Шпоры. 1. ЭВМ фон Неймана
Закон Фарадея
Согласно закону электромагнитной индукции Фарадея (в СИ):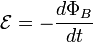
Где 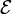 — электродвижущая сила, действующая вдоль произвольно выбранного контура, — электродвижущая сила, действующая вдоль произвольно выбранного контура,
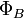 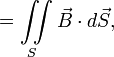 — магнитный поток через поверхность, натянутую на этот контур. — магнитный поток через поверхность, натянутую на этот контур.
Знак «минус» в формуле отражает правило Ленца, названное так по имени русского физика Э.Х.Ленца:
Индукционный ток, возникающий в замкнутом проводящем контуре, имеет такое направление, что создаваемое им магнитное поле противодействует тому изменению магнитного потока, которым был вызван данный ток.
Для катушки, находящейся в переменном магнитном поле, закон Фарадея можно записать следующим образом:
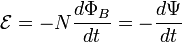
где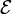 — электродвижущая сила, — электродвижущая сила,
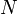 — число витков, — число витков,
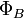 — магнитный поток через один виток, — магнитный поток через один виток,
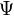 — потокосцепление катушки. — потокосцепление катушки.
Самоиндукция — возникновение ЭДС индукции в замкнутом проводящем контуре[1] при изменении тока, протекающего по контуру.
При изменении тока в контуре пропорционально меняется[2] и магнитный поток через поверхность, ограниченную этим контуром[3]. Изменение этого магнитного потока, в силу закона электромагнитной индукции, приводит к возбуждению в этом контуре индуктивной ЭДС.
Это явление и называется самоиндукцией. (Понятие родственно понятию взаимоиндукции, являясь как бы его частным случаем).
Направление ЭДС самоиндукции всегда оказывается таким, что при возрастании тока в цепи ЭДС самоиндукции препятствует этому возрастанию (направлена против тока), а при убывании тока — убыванию (сонаправлена с током). Этим свойством ЭДС самоиндукции сходна с силой инерции.
Величина ЭДС самоиндукции пропорциональна скорости изменения силы тока I:
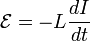 . .
32. магнитное поле в веществе. Магнитные моменты атомов. Типы магнетиков. Магнитный гистерезис. Точка Кюри.
При изучении магнитного поля в веществе различают 2 типа токов-макротоки и микротоки. Макротоки- электрические токи проводимости, а также конвекционные токи, связанные с движением заряженных макроскопических тел. Микротоки- токи, обусловленные движением электронов в атомах, ионах и молекулах. В веществе на магнитное поле макротоков накладывается дополнительное магнитное поле микротоков. Вектор магнитной индукции В характеризует результирующее магнитное поле в веществе,т.е. он равен геометрической сумме магнитных Индукций внешнего(В0) и внутреннего(Ввнутр)полей. Магнитное поле микротоков возникает в результате намагничивания магнетика при его помещение во внешнее магнитное поле. Поэтому первичным источником магнитного поля в веществе являются макротоки.
Вектором орбитального магнитного момента атома Pm называется векторная сумма орбитальных магнитных моментов всех его электронов: 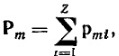 , Z-число электронов в атоме,равное порядковому номеру элемента в периодич.системе Менделеева. Аналогично этому, вектором орбитального момента импульса атома называется векторная сумма орбитальных моментов импульса всех электронов атома: , Z-число электронов в атоме,равное порядковому номеру элемента в периодич.системе Менделеева. Аналогично этому, вектором орбитального момента импульса атома называется векторная сумма орбитальных моментов импульса всех электронов атома: 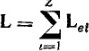 . Для атомных моментов Pm и L справедливо соотношение: . Для атомных моментов Pm и L справедливо соотношение: 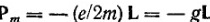 . .
Пусть намагничиваение ферромагнетика до насыщения(точка а) происходит по кривой оа. Если далее уменьшать напряженность Н намагничивающего поля, при этом намагниченность j изменяется по кривой, лежащей выше кривой ао. При Н=0 намагниченность отличается от 0:в ферромагнетике наблюдается остаточная намагниченность Jr,обусловленная тем, что и после прекращения внешнего поля у части доменов сохраняется преимущественная ориентация их магнитных моментов. Чтобы размагнититьобразец, следует создать магнитное поле с напряженностью, равной Hk(коэрцитивная сила), направленное в противоп.сторону. При дальнейшем увеличении магнитного поля, противоп.первоначальному, намагнич-ть образца снова достигает насыщения(b). Возвращаясь постепенно к напряженности намагнич-го поля +Нн, получим замкнутую кривую-петля гистерезиса.
Нарушение остаточной преимущественной ориентации областей спонтанной намагниченности может быть вызвана ударом иил сотрясением образца. С повышением температуры остаточная намагниченность ферромагнетика уменьшается. При достаточно высокой температуре, называемой точкой Кюри, она исчезает полностью. Это объясняется тем, что тепловое движение частиц ферромагнетика становится столь интенсивным, что области спонтанной намагниченности распадаются. Т.Кюри для железа-780, никеля-350, кобальта-1150 ⁰.
По магнитным свойствам магнетики подразделяются на три группы: диамагнетики, парамагнетики и ферромагнетики. Диамагнетики (например, цинк, золото, висмут) - это магнетики, у которых молекулы (атомы, ионы) не имеют результирующего магнитного момента 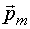 , или у которых индуцированный магнитный момент в атомных электронных оболочках под действием внешнего магнитного поля , или у которых индуцированный магнитный момент в атомных электронных оболочках под действием внешнего магнитного поля 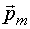 , значительно больше , значительно больше
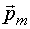 ( (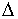 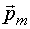 >> >> 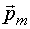 ). Парамагнетики (например, соли кобальта, никеля, платина) это магнетики, у которых молекулы (атомы, ионы) обладают постоянным магнитным моментом ). Парамагнетики (например, соли кобальта, никеля, платина) это магнетики, у которых молекулы (атомы, ионы) обладают постоянным магнитным моментом 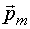 , не зависящим от внешнего магнитного поля. В отсутствии внешнего поля тепловое движение не допускает упорядоченной ориентации векторов , не зависящим от внешнего магнитного поля. В отсутствии внешнего поля тепловое движение не допускает упорядоченной ориентации векторов 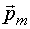 по полю. Ферромагнетики (например, железо, кобальт, никель) - это магнетики, у которых намагниченность зависит от напряженности магнитного поля по полю. Ферромагнетики (например, железо, кобальт, никель) - это магнетики, у которых намагниченность зависит от напряженности магнитного поля 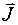 = f ( = f (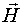 ). ).
|
33. Электрический колебательный контур. Дифференциальное уравнение электромагнитных колебаний. Энергия электромагнитных колебаний. Резонанс в колебательном контуре.
Электромагнитные колебания могут возникать в цепи, содержащей индуктивность L и емкость C. Такая цепь называется колебательным контуром. Возбудить колебания в таком контуре можно, например, предварительно зарядив конденсатор от внешнего источника напряжения, соединить его затем с катушкой индуктивности. Поскольку внешнее напряжение к контуру не приложено, сумма падений напряжений на емкости и индуктивности должна быть равна нулю в любой момент времени: 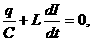 откуда, учитывая, что сила тока откуда, учитывая, что сила тока 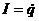 , получаем дифференциальное уравнение свободных незатухающих колебаний электрического заряда в колебательном контуре , получаем дифференциальное уравнение свободных незатухающих колебаний электрического заряда в колебательном контуре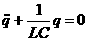 . Решением этого уравнения, как известно, является функция . Решением этого уравнения, как известно, является функция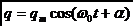 Таким образом, заряд на обкладках конденсатора изменяется по гармоническому закону с частотой ω0, называемой собственной частотой колебательного контура. Период колебаний определяется по формуле Томсона: Таким образом, заряд на обкладках конденсатора изменяется по гармоническому закону с частотой ω0, называемой собственной частотой колебательного контура. Период колебаний определяется по формуле Томсона: 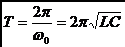 Дифференциальное уравнение свободных затухающих колебаний линейной системы определяется как Дифференциальное уравнение свободных затухающих колебаний линейной системы определяется как 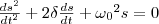
Явление резкого возрастания амплитуды силы тока в колебательном контуре при приближении циклической частоты вынуждающей ЭДС к значению Ωр называется явлением резонанса в электрической цепи, а частота Ωр-резонансной циклической частотой.. электрический резонанс наступает при частоте вынуждающей ЭДС несколько большей частоты свободных колебаний в цепи.
34.Энергия электромагнитных волн. Поток энергии. Вектор Умова-Пойнтинга.
Энергия электромагнитного поля выражается через объемную плотность энергии w, которая равна сумме объемных плотностей электрического (we) и магнитного (wm) полей. Для электрического поля плотность энергии можно найти по формуле 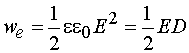 , где , где 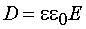 - электрическое смещение. Для магнитного поля плотность энергии можно найти по формуле: - электрическое смещение. Для магнитного поля плотность энергии можно найти по формуле: 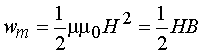 где где 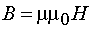 - магнитная индукция. Отсюда плотность энергии электромагнитного поля равна - магнитная индукция. Отсюда плотность энергии электромагнитного поля равна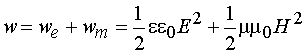 Так как векторы Так как векторы  и и  взаимно перпендикулярны и образуют с направлением волны правовинтовую систему, то направление вектора взаимно перпендикулярны и образуют с направлением волны правовинтовую систему, то направление вектора 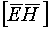 совпадает с направлением переноса энергии, а модуль этого вектора равен EH. Вектор плотности потока электромагнитной энергии называется вектором Умова-Пойнтинга и равен совпадает с направлением переноса энергии, а модуль этого вектора равен EH. Вектор плотности потока электромагнитной энергии называется вектором Умова-Пойнтинга и равен 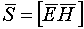 Вектор Вектор 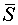 направлен в сторону распространения электромагнитной волны. Электромагнитные волны переносят энергию. При распространении волн возникает поток электромагнитной энергии. Плотностью потока или интенсивностью I называют электромагнитную энергию, переносимую волной за единицу времени через поверхность единичной площади: направлен в сторону распространения электромагнитной волны. Электромагнитные волны переносят энергию. При распространении волн возникает поток электромагнитной энергии. Плотностью потока или интенсивностью I называют электромагнитную энергию, переносимую волной за единицу времени через поверхность единичной площади: 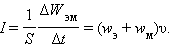
|
|
|
|
|
 Скачать 0.82 Mb.
Скачать 0.82 Mb.