Физика 9 класс. 1. Физика. Методы познания природы. Физические явления
 Скачать 5.42 Mb. Скачать 5.42 Mb.
|
19. Тепловое движение частиц. Температура-мера средней кинетической энергии частиц.Температура. Основное уравнение молекулярно-кинетической теории для идеального газа устанавливает связь легко измеряемого макроскопического параметра — давления — с такими микроскопическими параметрами газа, как средняя кинетическая энергия и концентрация молекул. Но, измерив только давление газа, мы не можем узнать ни среднее значение кинетической энергии молекул в отдельности, ни их концентрацию. Следовательно, для нахождения микроскопических параметров газа нужны измерения еще какой-то физической величины, связанной со средней кинетической энергией молекул. Такой величиной в физике является температура. Из повседневного опыта каждый знает, что бывают тела горячие и холодные. При контакте двух тел, из которых одно мы воспринимаем как горячее, а другое — как холодное, происходят изменения физических параметров как первого, так и второго тела. Например, твердые и жидкие тела обычно при нагревании расширяются. Через некоторое время после установления контакта между телами изменения макроскопических параметров тел прекращаются. Такое состояние тел называется тепловым равновесием. Физический параметр, одинаковый во всех частях системы тел, находящихся в состоянии теплового равновесия, называется температурой тела. Если при контакте двух тел никакие их физические параметры, например объем, давление, не изменяются, то между телами нет теплопередачи и температура тел одинакова. Термометры. В повседневной практике наиболее распространен способ измерения температуры с помощью жидкостного термометра. В устройстве жидкостного термометра используется свойство расширения жидкостей при нагревании. В качестве рабочего тела обычно применяется ртуть, спирт, глицерин. Чтобы измерить температуру тела, термометр приводят в контакт с этим телом; между телом и термометром будет осуществляться теплопередача до установления теплового равновесия. Масса термометра должна быть значительно меньше масоы тела, так как в противном случае процесс измерения может существенно изменить температуру тела. Изменения объема жидкости в термометре прекращаются, когда между телом и термометром прекращается теплообмен. При этом температура жидкости в термометре равна температуре тела. Отметив на трубке термометра положение конца столба жидкости при помещении термометра в тающий лед, а затем в кипящую воду при нормальном давлении и разделив отрезок между этими отметками на 100 равных частей, получают температурную шкалу по Цельсию. Температура тающего льда соответствует 0 °С (рис. 83), кипящей воды — 100 °C (рис. 84). Изменение длины столба жидкости в термометре на одну сотую длины между отметками 0 и 100 °С соответствует изменению температуры на 1 °С. Существенным недостатком способа измерения температуры с помощью жидкостных термометров является то, что шкала температуры при этом оказывается связанной с конкретными физическими свойствами определенного вещества, используемого в качестве рабочего тела в термометре,— ртути, глицерина, спирта. Изменение объема различных жидкостей при одинаковом нагревании оказывается несколько различным. Поэтому ртутный и глицериновый термометры, показания которых совпадают при 0 и 100 °С, дают разные показания при других температурах. Газы в состоянии теплового равновесия. Для того чтобы найти более совершенный способ определения температуры, нужно найти такую величину, которая была бы одинаковой для любых тел, находящихся в состоянии теплового равновесия. Экспериментальные исследования свойств газов показали, что для любых газов, находящихся в состоянии теплового равновесия, отношение произведения давления газа на его объем к числу молекул оказывается одинаковым: Этот опытный факт позволяет принять величину в качестве естественной меры температуры. Так как , то с учетом основного уравнения молекулярно-кинетической теории (24.2) получим Следовательно, средняя кинетическая энергия молекул любых газов, находящихся в тепловом равновесии, одинакова. Величина равна двум третям средней кинетической энергии беспорядочного теплового движения молекул газа и выражается в джоулях. В физике обычно выражают температуру в градусах, принимая, что температура T в градусах и величина связаны уравнением где k — коэффициент пропорциональности, зависящий от выбора единицы температуры. Отсюда получаем Последнее уравнение показывает, что имеется возможность выбрать температурную шкалу, не зависящую от природы газа, используемого в качестве рабочего тела. Практически измерение температуры на основании использования уравнения (25.4) осуществляется с помощью газового термометра (рис. 85). Устройство его таково: в сосуде постоянного объема находится газ, количество газа остается неизменным. При постоянных значениях объема V и числа молекул N давление газа, измеряемое манометром, может служить мерой температуры газа, а значит, и любого тела, с которым газ находится в тепловом равновесии. 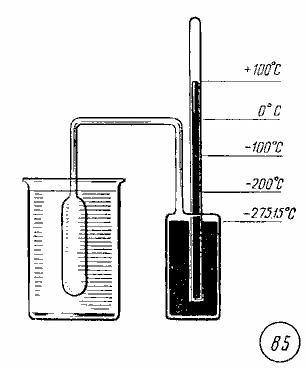 Абсолютная шкала температур. Шкала измерения температуры в соответствии с уравнением (25.4) называется абсолютной шкалой. Ее предложил английский физик У. Кельвин (Томсон) (1824—1907), поэтому шкалу называют также шкалой Кельвина. До введения абсолютной шкалы температур в практике получила широкое распространение шкала измерения температуры по Цельсию. Поэтому единица температуры по абсолютной шкале, называемая кельвином (К), выбрана равной одному градусу по шкале Цельсия: 1 К = 1 °С. (25.5) Абсолютный нуль температуры. В левой части уравнения (25.4) все величины могут иметь только положительные значения или быть равными нулю. Поэтому абсолютная температура T может быть только положительной или равной нулю. Температура, при которой давление идеального газа при постоянном объеме должно быть равно нулю, называется абсолютным нулем температуры. Постоянная Больцмана. Значение постоянной k в уравнении (25.4) можно найти по известным значениям давления и объема газа с известным числом молекул N при двух значениях температуры T0 и T1: Как известно, 1 моль любого газа содержит примерно молекул и при нормальном давлении занимает объем . Опыты показали, что при нагревании любого газа при постоянном объеме от 0 до 100° С его давление возрастает от до . Подставляя эти значения в уравнение (25.6), получаем до . Подставляя эти значения в уравнение (25.6), получаем Коэффициент k - называется постоянной Болъцмана, в честь австрийского физика Людвига Больцмана (1844—1906), одного из создателей молекулярно-кинетической теории. Связь абсолютной шкалы и шкалы Цельсия. Уравнение (25.4) позволяет по известному значению объема V0 одного моля газа при температуре 0 °С и нормальном давлении и найденному значению постоянной Больцмана установить связь между значениями температуры t по шкале Цельсия и температуры T по абсолютной шкале. При температуре 0 °С температура T по абсолютной шкале равна Мы получили, что температура 0 °С по шкале Цельсия соответствует температуре 273 К по абсолютной шкале. Так как единица температуры по абсолютной шкале 1 К выбрана равной единице температуры по шкале Цельсия 1 °С, то при любой температуре t по Цельсию значение абсолютной температуры T выше на 273 градуса: T = t + 273 . (25.7) Из уравнения (25.7) следует, что абсолютный нуль соответствует — 273 °С (более точно, — 273,15 °С). Соответствие шкалы Цельсия и абсолютной шкалы температур представлено на рисунке 86. 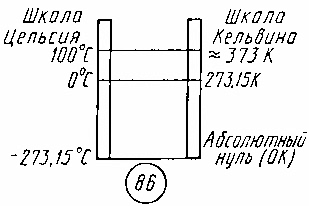 Температура — мера средней кинетической энергии молекул. Из уравнений (25.2) и (25.4) следует равенство . (25.8) Средняя кинетическая энергия хаотического движения молекул газа пропорциональна абсолютной температуре. Из уравнений (24.2) и (25.8) можно получить, что p = nkT. (25.9) Уравнение (25.9) показывает, что при одинаковых значениях температуры и концентрации молекул давление любых газов одинаково, независимо от того, из каких молекул они состоят. |
