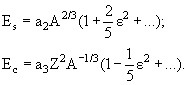Физика 9 класс. 1. Физика. Методы познания природы. Физические явления
 Скачать 5.42 Mb. Скачать 5.42 Mb.
|
84. Энергия связи атома. Связь массы частицы и энергии.Под энергией связи атомного ядра понимают энергию, которую нужно затратить, чтобы расщепить ядро на отдельные нуклоны. Такая же энергия выделяется при образовании ядра из свободных нуклонов. Ее можно рассчитать, пользуясь формулой Л. Эйнштейна, связывающей массу частицы и энергию: W=mc2 После создания масс-спектрографа можно было с большой точностью (до 0,01 %) измерить массы всех изотопов элементов таблицы Менделеева, что и сделано учеными. Анализ этих данных показывает, что для всех элементов масса покоя ядра меньше, чем сумма масс покоя составляющих его нуклонов, если последние находятся в свободном состоянии. Это различие может быть охарактеризовано величиной Δm=∑mn−nja=Zmp+(A−Z)mn−mja, которая носит название дефекта масс. Уменьшение массы при образовании ядра из свободных частиц означает, что при этом уменьшается энергия этой системы частиц на величину энергии связи Wsv=Δmc2=(Zmp+(A−Z)mn−mja)c2. Энергия связи определяется величиной работы, которую нужно совершить для расщепления ядра на составляющие его нуклоны. Но куда расходуется эта энергия? При образовании ядра из нуклонов последние за счет действия ядерных сил на малых расстояниях устремляются друг к другу с огромными ускорениями. Излучаемые при этом γ-кванты обладают энергией связи Wsv, т.е. при образовании ядер из нуклонов эта энергия связи выделяется. Энергия связи очень велика (ее обычно выражают в МэВ: 1 МэВ = 106 эВ = = 1,6 ⋅ 10-13 Дж). Об этой величине можно судить по такому примеру: образование 4 г гелия сопровождается выделением такой же энергии, как при сгорании 5—6 вагонов каменного угля. Важной характеристикой ядра служит средняя энергия связи ядра, приходящаяся на один нуклон (так называемая удельная энергия связи ядра), ωsv=WsvA Чем она больше, тем сильнее связаны между собой нуклоны, тем прочнее ядро. Эту удельную энергию связи ωsv всегда можно подсчитать. Результаты показывают, что для большинства ядер ωsv≈8 МэВ и уменьшается для очень легких и очень тяжелых ядер. По мере увеличения числа нуклонов в ядре возрастают кулоновские силы отталкивания между протонами, ослабляющие связи в ядре, и величина ωsv у тяжелых ядер уменьшается. Величина ωsv максимальна у ядер средней массы (А = 50...60), следовательно, они отличаются наибольшей прочностью (рис. 22.1). 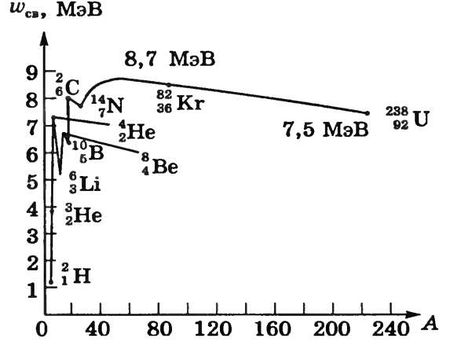 Рис. 22.1 Процессы деления тяжелых ядер и синтеза легких являются энергетически выгодными, потому что сопровождаются возрастанием энергии связи, т.е. выделением энергии. На этом основано, как мы увидим ниже, получение атомной энергии при делении тяжелых ядер и термоядерной энергии — при синтезе легких. 1. Энергии связи и массы ядер Масса стабильных ядер меньше суммы масс входящих в ядро нуклонов, разность этих величин и определяет энергию связи ядра:
В (1.1) MN(A,Z) – масса ядра, Z – число протонов в ядре, А – число нуклонов. Однако в таблицах масс приводятся, как правило, не массы ядер, а массы нейтральных атомов либо величины «избытков масс» Δ = M – A, где М – масса нейтрального атома в МэВ. Это связано, в первую очередь, с методикой измерения масс с помощью масс-спектрометров. Часто массы нейтральных атомов приводят в единицах
В банке ядерных данных www.nndc.bnl.gov собраны значения «избытков масс» Δ = M – A (см. также приложение к сборнику задач «Субатомная физика», изд. МГУ, 1994 и банк данных об основных состояниях ядер cdfe.sinp.msu.ru/services/gsp.en.html). Величина А представляет собой в данном случае произведение числа нуклонов на значение единицы массы (1.2) в МэВ. Таким образом, величины Δ приводятся в единицах МэВ, что удобно для проведения расчетов.
Для примера вычислим величину энергии связи и удельной энергии связи ядра 12С двумя способами: а) пользуясь таблицей масс в единицах (1.1) и б) используя таблицу избытков масс Δ = M – A. Прежде всего, необходимо преобразовать формулу (1.1), заменив массы ядер MN на массы нейтральных атомов М:
Формула (1.3) является приближенной – в ней опущены энергии связи электронов в атомах. Однако поскольку энергии связи нуклонов в ядре на 5 – 6 порядков превышают энергии связи электронов в атомах, это приближение не скажется на точности дальнейших расчетов энергий связи ядер. Прибавляя и вычитая Zme в (1.3), получим для энергии связи нуклонов в ядрах
Для ядра 12С по первому способу Eсв = [6·1.007825 + 6·1.008665 – 12.00000]×931.5 МэВ Для использования таблиц для Δ = M – A преобразуем (1.4)
Для энергии связи 12С расчет этим способом проще: Eсв = 6·7.289 МэВ + 6·8.071 – 0 = 92.16 МэВ. Поэтому в дальнейших расчетах будет использоваться именно второй способ, основанный на таблицах для избытков масс Δ = M – A. Удельная энергия связи, т.е. энергия связи на один нуклон, для ядра 12С составляет
Зависимость удельной энергии связи от числа нуклонов А является наиболее важным для приложений экспериментальным результатом физики ядра (рис.1.1).
Экспериментально установленное распределение удельных энергий связи ядер по значениям чисел нуклонов в ядре А имеет следующие характерные черты: В широкой области ядер удельная энергия связи ε слабо зависит от А; Для ядер с малыми А удельная энергия имеет «спад». Для тяжелых ядер средняя удельная энергия связи меньше, чем для средних, причем с ростом А наблюдается снижение ее величины. Для ядер с Z = N удельная энергия выше, чем для других ядер с тем же значением А. Четно-четные (по Z и N) ядра имеют в среднем большие значения ε, чем нечетно-четные, а нечетно-нечетные – меньшие. Теоретическое объяснение этого распределения дает модель заряженной жидкой капли и соответствующая этой модели формула Вайцзеккера. Первая из перечисленных (и главная) особенность распределения удельных энергий связи ядер – следствие насыщения ядерных сил и их короткого радиуса действия. Вторая связана с тем, что связи нуклонов, находящихся на поверхности ядра, с другими нуклонами ядра не полностью насыщены. Чем больший процент нуклонов находится на поверхности ядра, тем больше «убыль» энергии насыщения (этими особенностями ядерные силы оказываются подобны силам, действующим между молекулами жидкости). Третья особенность распределения удельной энергии связи объясняется тем, что протоны ядер участвуют не только в сильном (ядерном), но и в электромагнитном взаимодействии. Чем больше протонов, тем выше энергия кулоновского отталкивания. Четвертая и пятая особенности распределения – следствия оболочечной структуры ядра и симметрии, связанной с реализацией в ядре принципа Паули. Учет всех перечисленных свойств приводит к полуэмпирической формуле Вайцзеккера или модели заряженной жидкой капли (von Weizsäcker, 1935):
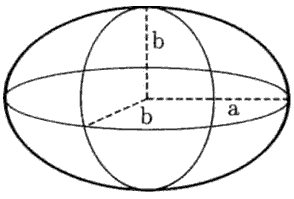
Коэффициенты в (1.7) подбираются из условий наилучшего совпадения кривой модельного распределения с экспериментальными данными. Поскольку такая процедура может быть проведена по-разному, существует несколько наборов коэффициентов формулы Вайцзеккера. Часто используются в (1.7) следующие: a1 = 15.6 МэВ, a2 = 17.2 МэВ, a3 = 0.72 МэВ, a4 = 23.6 МэВ,  Несложно оценить значение зарядового числа Z, при котором ядра становятся нестабильными по отношению к спонтанному распаду. Спонтанный распад ядра возникает в случае, если кулоновское расталкивание протонов ядра начинает преобладать над стягивающими ядро ядерными силами. Оценка ядерных параметров, при которых наступает такая ситуация, может быть проведена из рассмотрения изменений в поверхностной и кулоновской энергиях при деформации ядра. Если деформация приводит к более выгодному энергетически состоянию, ядро будет спонтанно деформироваться вплоть до деления на два фрагмента. Количественно такая оценка может быть проведена следующим образом. При деформации ядро, не меняя своего объема, превращается в эллипсоид с осями (см. рис. 1.2):
При деформации первый член формулы (1.7) не меняется, второй (поверхностная энергия) Es - по абсолютной величине возрастает, а третий (кулоновская энергии) Ec - уменьшается:
Таким образом, деформация изменяет полную энергию ядра на величину
Здесь учтен знак (-) второго и третьего членов в (1.7). Если величина изменения энергии (1.9) положительна, энергия связи ядра будет расти, т.е. деформация будет энергетически выгодна, и спонтанное деление возможно. Спонтанное деление неизбежно, когда значения (1.9) становятся больше нуля, т.е. при значениях
Следует подчеркнуть приближенный характер полученного результата как следствия классического подхода к квантовой системе – ядру. 2. Энергии отделения нуклонов и кластеров от ядра Энергия отделения нейтрона от ядра равна Eотд.n = M(A–1,Z) + mn – M(A,Z) = Δ(A–1,Z) + Δn – Δ(A,Z). Энергия отделения протона Eотд.p = M(A–1,Z–1) + M(1H) – M(A,Z) = Δ(A–1,Z–1) + Δ(1H) – Δ(A,Z). Следует отметить, что поскольку основными данными о массах ядер являются таблицы «избытков» масс Δ, расчеты энергий отделения удобнее проводить с помощью этих величин.
Eотд.n(12C) = Δ(11C) + Δn – Δ(12C) = 10.65 МэВ + 8.07 МэВ – 0 = 18.72 МэВ. Eотд.p(12C) = Δ(11B) + Δ(1H) – Δ(12C) = 8.668 МэВ + 7.289 МэВ – 0 = 15.96 МэВ.
Eотд.α = M(A–4,Z–2) + M(4He) – M(A,Z) = Δ(A–4,Z–2) + Δ(4He) – Δ(A,Z). Eотд.α(12C) = Δ(8Be) + Δ(4He) – Δ(12C) = (4.941 + 2.424 – 0) МэВ = 7.365 МэВ. Сравним результаты, полученные для удельной энергии связи ядра 12Си энергий отделения от него нейтрона и протона. Энергия отделения одного нуклона от этого ядра оказалась вдвое выше удельной энергии связи! Энергия одновременного отделения кластера из 4 нуклонов - α-частицы оказалась меньшеудельной энергии связи – т.е. средней энергии отделения одного нуклона. Эти факты и аналогичные результаты для ряда других ядер были объяснены в теоретических моделях ядер. Аналогичные расчеты для ядер 11B, 13С, 13N, 14С показывают, что ядро 12С обладает особой устойчивостью по сравнению с соседними (по А) ядрами. Эти результаты сведены в Таблицу 1.
|