геодезия экз. экз гео. 1. Форма и размеры Земли (физ поверхность, геоид, эллипсоид)
 Скачать 0.8 Mb. Скачать 0.8 Mb.
|
|
Карта – уменьшенное и закономерно искаженное вследствие влияния кривизны Земли изображение на бумаге горизонтальной проекции значительной части или всей земной поверхности. Степень уменьшения больше по сравнению с планом: 10000 раз, 50000….. . Искажения происходят из–за невозможности развертывания сферических поверхностей (геоид, эллипсоид) в плоскость (бумага плоская) без разрывов и складок. На картах наносят градусные и километровые сетки. Все карты контурно – высотные (топографические). По планам и картам можно решать ряд задач: Определение расстояний между точками. Определение прямоугольных и географических координат точек. Определение абсолютных отметок точек. Ориентирование линий местности. Построение профилей по заданным направлениям. Определение крутизны ската. Определение водосборной площади и другие. Профиль местности есть линия пересечения земной поверхности с отвесной (вертикальной) плоскостью, расположенной в заданном направлении (PQ).Его уменьшенное изображение на бумаге также называется профилем. Направление сечения может быть прямолинейным, ломаным или криволинейным. 7. Прямая и обратная геодезические задачи Прямая геодезическая задача заключается в том, что по известным координатам одной точки, дирекционному углу и расстоянию до другой определяют координаты последней. При вычислениях чаще всего дирекционные углы переводят в румбы. Прямая геодезическая задача решается и при вычислении координат вершин полигонов. Дано: х1; у1 – координаты начальной точки; α1-2; α2-3; α3-4; α4-5; α5-1 - дирекционные углы сторон полигона. d1-2; d2-3……d5-1 - горизонтальные проложения сторон полигона. Найти: х2 и у2; х3 и у3…..х5 и у5. Разница между координатами соседних точек называется приращением координат: х2 – х1=Δх1-2; у2 – у1=Δу1-2. Отсюда х2=х1+Δх1-2; у2=у1+Δу1-2. 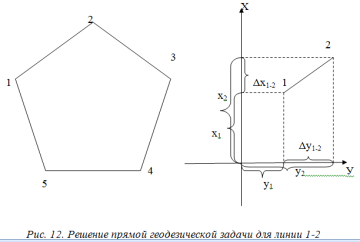 Из треугольника следует : Δх1-2=d1-2∙cosr1-2; Δу1-2= d1-2∙sinr1-2. 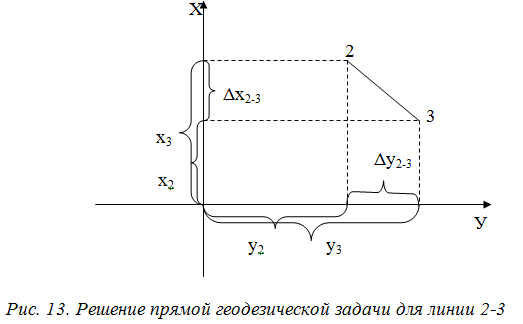 Из рисунка следует: х3=х2+Δх2-3; у3=у2+Δу2-3; Δх2-3=d2-3∙cosr2-3; Δу2-3= d2-3∙ sinr2-3. Перейдем к общему случаю: хn=хn-1+Δхn; уn =уn-1+Δуn; Δхn= dn∙cosrn; Δуn= dn sinrn. При вычислениях учитываются знаки приращений координат в зависимости от четверти, в которую направлена линия . Если использовать дирекционные углы, то знаки перед приращениями координат получаются сами собой. Координаты n – ой точки полигона можно выразить и через координаты первой точки. х2=х1+Δх1-2 х3=х2+Δх2-3=х1+ (Δх1-2+ Δх2-3) х4=х3+Δх3-4= х1+ (Δх1-2+ Δх2-3+ Δх3-4) хn= х1+ 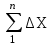 и уn=у1+ и уn=у1+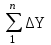 ; ;здесь суммы приращений координат. Отсюда запишем: хn - х1= 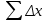 уn – у1= уn – у1= 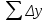 . .В случае замкнутого полигона, когда, обойдя все вершины поочередно, мы возвращаемся в исходную, хn - х1=0 и уn – у1=0. 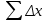 теор.=0 и теор.=0 и 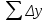 теор.=0. теор.=0.Однако в связи с ошибками в угловых и линейных величинах эта сумма будет несколько отличаться от 0. Мы возвратимся не в точку 1, а в 1΄.Полученная разница в суммах приращений координат называется невязкой. 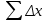 изм.=fх≠0 – невязка по х; изм.=fх≠0 – невязка по х;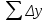 изм.=fу ≠0 – невязка по у. изм.=fу ≠0 – невязка по у.Для оценки точности полигона вычисляют абсолютную невязку: (1 - 1΄)=fабс.= 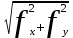 , , а затем относительную ошибку: fотн.= 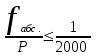 ; Р – периметр. ; Р – периметр.Если условие неравенства выполняется, полученную невязку по осям координат распределяют в вычисленные приращения в виде поправок, с обратным невязке знаком, пропорционально значениям горизонтальных проложений: большую поправку в большее значение проложения. Обратная геодезическая задача заключается в вычислении дирекционного угла и горизонтального проложения линии, по известным координатам ее начальной и конечной точек. Из предыдущих рисунков видно, что d= 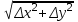 ; tgr= ; tgr=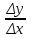 ; r=arctgr; ; r=arctgr; d= 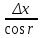 = =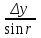 . .Дирекционный угол находят по полученному румбу, учитывая четверть, в которую направлена прямая. Четверть определяется по знакам приращений координат: 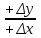 1 четверть α=r; 1 четверть α=r; 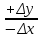 2 четверть α=180° - r; 2 четверть α=180° - r;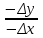 3 четверть α=r+180°; 3 четверть α=r+180°; 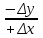 4 четверть α=360° - r. 4 четверть α=360° - r. 9. Задачи, решаемые на планах и картах. По планам и картам можно решать ряд задач: Определение расстояний между точками. Определение прямоугольных и географических координат точек. Определение абсолютных отметок точек. Ориентирование линий местности. Построение профилей по заданным направлениям. Определение крутизны ската. Определение водосборной площади и другие. 1.Физическая поверхность – совокупность всех неровностей суши и дна океанов, а также поверхности воды. Она не может быть выражена конечным математическим уравнением, поэтому используется для решения лишь некоторых практических задач геодезии. 2.Уровенная поверхность – поверхность воды Мирового океана в спокойном состоянии, мысленно продолженная под материками. В 1873 году немецкий ученый Листинг назвал ее поверхностью геоида. Океаны составляют 71%, суша – 29%. Поверхность воды всюду горизонтальна, т.е. перпендикулярна к отвесным линиям (направление силы тяжести). Поверхность суши и дна океанов изучают относительно поверхности геоида. Расстояния от точек физической поверхности Земли до уровенной поверхности по направлению отвесных линий называют высотами точек, а их числовое выражение называют отметками. Они могут быть положительными и отрицательными. В России за поверхность, совпадающую с геоидом, принята поверхность Балтийского моря (ноль Кронштадского футштока). Высоты, отсчитываемые от уровня Балтийского моря, называются абсолютными, от другой какой – либо уровенной поверхности – условными. Геоид пригоден для решения практических задач. Для теоретических расчетов он не пригоден, так как не имеет конечного математического выражения из-за непостоянства направления отвесных линий вследствие неравномерного распределения масс внутри Земли. Кроме того, уровень поверхности воды в различных океанах различен; имеются приливы и отливы. 3.Поверхность эллипсоида вращения получается при вращении эллипса вокруг малой (полярной) полуоси. Эллипсоид характеризуется тремя величинами: а – большая полуось, в – малая полуось,  . .Эллипсоид ориентируется в теле Земли определенным образом. Постановлением Совета министров СССР в апреле 1946 года в нашей стране для геодезических работ принят эллипсоид Красовского Ф.Н. Его размеры: а=6378245 м, в=6356863 м. Эллипсоид, относительно которого ведутся все геодезические работы в данной стране, называется референц-эллипсоид. 4. Для решения многих практических задач достаточно за фигуру Земли принять шар с радиусом R=6371 км. 10.Масштабы:численый,линейный поперечный,словесный. Масштаб - степень уменьшения горизонтальных проложений линий местности при изображении их на плане или карте Численный масштаб есть отвлеченная дробь, числителем которой является единица, а знаменателем – число, показывающее во сколько раз уменьшены горизонтальные проложения линий местности при изображении их на плане или карте (иначе – отношение горизонтального проложения линии на плане или карте к горизонтальному проложению той же линии на местности,)1:М; 1:100; 1:2000; 1:1000 Именованный (словесный) масштаб можно выразить словами: в 1см карты содержится 20 м местности (М 1:2000); в 1см – 100м (М 1:10000). Если горизонтальное проложение линии на местности обозначить S, на плане – d, то можно записать: d = S/M или S=d·M (пусть d=1 см, S=10 м; 1: М=1:1000).Чем больше М, тем мельче масштаб, чем меньше М, тем масштаб крупнее.1:50000 мельче 1:25000 вдвое и т.д. Линейный масштаб строится графически. Он служит для ускорения работ по переходу от измерений на местности к измерениям на плане (карте) и обратно при большом объеме работ. Он строится путем откладывания равных отрезков, называемых основанием масштаба ,вдоль прямой линии и оцифровкой правых концов отрезков, начиная со второго, в соответствии с численным масштабом. Для повышения точности измерений первое основание делят на мелкие части, на концах которого ставят нуль. Доли мелких делений оценивают на глаз. Линейный масштаб не отличается высокой точностью. Поперечный масштаб является также графическим изображением численного масштаба, строится он на основе линейного масштаба, но отличается более высокой точностью. Для построения поперечного масштаба из концов оснований линейного масштаба восстанавливают перпенди-куляры, на двух крайних из них откладывают n равных отрезков и через одноименные точки проводят прямые, параллельные линии линейного масштаба. Первые нижнее и верхнее основания делят на m равных частей, нулевую точку нижнего основания соединяют с первой точкой верхнего основания, а через все остальные проводят линии, параллельные только что проведенной. Эти линии называются трансверсалями. 11.Условные знаки планов и карт Понятие местность при изображении ее на планах и картах объединяет два более конкретных понятия: рельеф (совокупность неровностей поверхности Земли) и ситуация (совокупность местных предметов, сооружений, угодий, водных объектов и т.д.). При составлении планов и карт для обозначения ситуации и рельефа пользуются условными знаками (их насчитывается более 500). Условные знаки ситуации делятся на четыре вида: контурные (масштабные), внемасштабные, пояснительные и линейные. 1.Условные контурные знаки служат для изображения местных предметов, выражающихся в масштабе карты (плана). При этом сначала пунктиром или сплошной линией вычерчивается контур предмета, который затем заполняется значками. Примерами таких знаков могут служить знаки, изображающие дома, границы различных контуров. 2.Условные внемасштабные знаки служат для изображения важных местных предметов, не изображающихся в масштабе карты из-за малости своих размеров. Определенная точка в каждом знаке соответствует положению предмета на местности (это может быть центр, вершина, основание, угол знака). По этим условным знакам нельзя судить о величине предметов местности (километровые столбы, ветряные двигатели, памятники, радиомачты). 3.Условные пояснительные знаки дополняют характеристику изображенных на карте предметов. 4,Линейные сооружения, ручьи выделяют в условные знаки, называемые линейными. Те же предметы на плане (в крупном масштабе) могут изображаться масштабными знаками. 5,Условные знаки рельефа вычерчиваются всегда коричневым цветом. Они включают горизонтали, бергштрихи и специальные знаки для отдельных форм рельефа (овраги, скалы, террасы, промоины и т.д.), невыражаемых горизонталями. 12. Изображение рельефа горизонталями Рельефом называется совокупность неровностей земной поверхности. При строительстве и эксплуатации различных объектов рельеф часто имеет решающее значение. Для изображения рельефа предложены различные способы (отмывка, штриховка и т. д.). На современных топографических картах и планах, применяемых для решения инженерных задач, рельеф изображается горизонталями. Существо метода заключается в следующем. Прежде всего определяется высота характерных точек над уровенной поверхностью (рис. 1.19). Численное значение высоты точки называется отметкой. Имея отметки характерных точек, по определенным правилам строят горизонтали.  При проведении практических съемок часто оказывается целесообразным определять отметки не относительно основной, а относительно условно принятой уровенной поверхности. Тогда отметки в первом случае называются абсолютными, во втором – условными (HA,НВ –абсолютные отметки;HD, НC –условные). В Российской Федерации основная (исходная) уровенная поверхность зафиксирована кронштадтским футштоком. По многолетним наблюдениям за уровнем моря в Кронштадте был установлен средний уровень. В гранитном устое моста через канал закреплена медная пластина, на ней чертой зафиксирован средний уровень. Эту черту именуют нулем кронштадтского футштока. Относительно уровенной поверхности, проходящей через нуль кронштадтского футштока, и определяются абсолютные отметки на всей территории страны. Условные поверхности (и соответственно условные отметки) применяются для различных участков местности независимо.Точки физической поверхности Земли характеризуются различными отметками. Но если известны отметки двух точек, то можно вычислить превышение одной точки над другой (относительную высоту). Так, превышение точки В над точкойА(рис. 1.19) составит:h = НВ –НА. Метод горизонталей позволяет определить отметки любых точек топографической карты или плана. Построение горизонталей осуществляется исходя из следующего. При проведении практических съемок часто оказывается целесообразным определять отметки не относительно основной, а относительно условно принятой уровенной поверхности. Тогда отметки в первом случае называются абсолютными, во втором – условными (HA,НВ –абсолютные отметки;HD, НC –условные). В Российской Федерации основная (исходная) уровенная поверхность зафиксирована кронштадтским футштоком. По многолетним наблюдениям за уровнем моря в Кронштадте был установлен средний уровень. В гранитном устое моста через канал закреплена медная пластина, на ней чертой зафиксирован средний уровень. Эту черту именуют нулем кронштадтского футштока. Относительно уровенной поверхности, проходящей через нуль кронштадтского футштока, и определяются абсолютные отметки на всей территории страны. Условные поверхности (и соответственно условные отметки) применяются для различных участков местности независимо.Точки физической поверхности Земли характеризуются различными отметками. Но если известны отметки двух точек, то можно вычислить превышение одной точки над другой (относительную высоту). Так, превышение точки В над точкойА(рис. 1.19) составит:h = НВ –НА. Метод горизонталей позволяет определить отметки любых точек топографической карты или плана. Построение горизонталей осуществляется исходя из следующего.Пусть имеется некоторая возвышенность (рис. 1.20, а), которую пересекает поверхность, параллельная уровенной и расположенная от нее на высотеH1. Линия пересечения физической поверхности Земли будет замкнутой кривой, и, будучи спроектированной на горизонтальную плоскость, эта линия, называемая горизонталью, характеризует данную возвышенность на отметкеH1.Если для той же возвышенности секущую поверхность примем на высоте H2 (рис. 1.20, б), то получим другую горизонталь, характеризующую возвышенность на этой высоте.  Для того чтобы получить достаточно детальную характеристику данной формы рельефа, следует задать необходимое количество секущих поверхностей через равные промежутки по высоте hc.(рис. 1.21).Каждая поверхность и соответственно каждая горизонталь характеризуется определенной отметкой. Отсюда определение: горизонтали – линии, соединяющие точки земной поверхности с одинаковыми отметками.  Расстояние между горизонталями в плане d называется заложением горизонталей (см. рис. 1.22).  Расстояние между секущими поверхностями по высоте, т.е. разность отметок двух последовательных горизонталей hcназывается высотой сечения рельефа. В зависимости от масштаба, вида рельефа и назначения плана или карты применяютhc = 0,25; 0,5; 1; 2; 2,5; 5 м и др. Чем меньше высота сечения рельефа, тем точнее должны быть выполнены работы по съемке рельефа.Для изображения отдельных деталей рельефа применяют полугоризонтали в том случае, если это не удается сделать при помощи основных горизонталей. Их проводят через hc/2, вычерчивают прерывистыми линиями (см. рис. 1.21).Горизонтали всегда проводят кратными принятой высоте сечения рельефа. Так, если hc = 0,5 м, то возможны следующие отметки горизонталей: 16,5; 17; 17,5 м и т.п. Если hc = 2м, то, соответственно, 24; 26; 28 м ...Для лучшего чтения рельефа часть горизонталей вычерчивают утолщенной линией: при hc= 0,25; 0,5; 2,5 м обычно утолщается каждая четвертая горизонталь (соответственно кратные 1; 2; 10 м); приhc= 1; 2; 5; 10 м утолщается каждая пятая или десятая (соответственно кратная 5; 10; 25; 50 м). У утолщенных горизонталей выписывают их отметки, располагая цифры в разрывах горизонталей так, чтобы их верх был направлен в сторону возвышения. Дополнительно направления скатов указывают берг-штрихами (рис. 1.22). Расстояние между секущими поверхностями по высоте, т.е. разность отметок двух последовательных горизонталей hcназывается высотой сечения рельефа. В зависимости от масштаба, вида рельефа и назначения плана или карты применяютhc = 0,25; 0,5; 1; 2; 2,5; 5 м и др. Чем меньше высота сечения рельефа, тем точнее должны быть выполнены работы по съемке рельефа.Для изображения отдельных деталей рельефа применяют полугоризонтали в том случае, если это не удается сделать при помощи основных горизонталей. Их проводят через hc/2, вычерчивают прерывистыми линиями (см. рис. 1.21).Горизонтали всегда проводят кратными принятой высоте сечения рельефа. Так, если hc = 0,5 м, то возможны следующие отметки горизонталей: 16,5; 17; 17,5 м и т.п. Если hc = 2м, то, соответственно, 24; 26; 28 м ...Для лучшего чтения рельефа часть горизонталей вычерчивают утолщенной линией: при hc= 0,25; 0,5; 2,5 м обычно утолщается каждая четвертая горизонталь (соответственно кратные 1; 2; 10 м); приhc= 1; 2; 5; 10 м утолщается каждая пятая или десятая (соответственно кратная 5; 10; 25; 50 м). У утолщенных горизонталей выписывают их отметки, располагая цифры в разрывах горизонталей так, чтобы их верх был направлен в сторону возвышения. Дополнительно направления скатов указывают берг-штрихами (рис. 1.22).  13. Устройство и типы теодолитов. Назначение его основных частей. Отсчетные устройства: виды микроскопов. устройство на примере теодолита 2Т30. Его основными составными частями являются: 1 – кремальера, для получения четкого изображения визирной цели; 2 – закрепительный винт зрительной трубы; 3 – визир, для приближенного наведения на цель; 4- закрепительный винт лимба горизонтального круга; 5 – юстировочный винт цилиндрического уровня, для исправления положения пузырька уровня; 6 - закрепительный винт алидады; 7 – цилиндрический уровень при алидаде для горизонтирования прибора, то есть для приведения его оси вращения в отвесное положение; 8 - горизонтальный круг, для измерения горизонтальных углов; 9 – вертикальный круг для измерения вертикальных углов;10 - зрительная труба. Закрепительные винты служат для закрепления соответственных частей, наводящие – для точного наведения на цель, то есть для их малых, но точных перемещений.1 – наводящий винт лимба горизонтального круга; 2 – окуляр микроскопа, для взятия отсчетов по лимбам; 3 – зеркало подсветки, для освещения поля зрения микроскопа; 4 – боковая крышка; 5 – посадочный паз для буссоли; 6 – уровень при трубе; 7 – юстировочная гайка; 8 – колпачок; 9 - диоптрийное кольцо окуляра; 10 – наводящий винт трубы; 11 – наводящий винт алидады; 12 – подставка – основание прибора; 13 – подъемные винты (3 штуки), для горизонтирования прибора при помощи цилиндрического уровня; 14 – втулка; 15 – основание; 16 – крышка. Лимб горизонтального круга представляет собой стеклянный круг, проградуированный по часовой стрелке от 0°до 360°. Цена деления равна 1°. Алидада представляет собой стеклянную пластинку, расположенную сносно с лимбом. Эта «линия нулей» фиксирует на лимбе отдельные положения зрительной трубы и выполняет функцию отсчетного устройства. Зрительная труба состоит из объектива, служащего для формирования изображения цели;окуляра–для увеличения изображения; кремальеры для получения четкого изображения цели;На трубе имеется оптический визир для приближенного наведения на цель  Основными осями теодолита являются ОО – основная ось вращения прибора, проходит через точку пересечения визирной оси и горизонтальной оси вращения трубы и через центр лимба горизонтального круга; SS - горизонтальная ось вращения зрительной трубы; UU – ось цилиндрического уровня, мнимая прямая, касательная к внутренней поверхности ампулы в средней ее точке; VV – визирная ось зрительной трубы, мнимая прямая, проходящая через перекрестье сетки нитей и центр объектива. |
