Расчет плиты ребрестой. Расчет плиты ребристой. 1. Исходные данные Расчет ребристой плиты
 Скачать 0.87 Mb. Скачать 0.87 Mb.
|
|
сечения плиты Поперечное сечение плиты представлено на рис. 5. 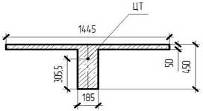 Рисунок 4 – Расчетное сечение плиты Площадь приведенного сечения плиты: Статический момент приведенного сечения относительно нижней грани: Расстояние от нижней грани до центра тяжести приведенного сечения: Момент инерции приведенного сечения:  Момент сопротивления приведенного сечения по нижней зоне: Момент сопротивления приведенного сечения по верхней зоне: Расстояние от ядровой точки, наиболее удаленной от растянутой грани, до центра тяжести сечения: Где Принимаем Расстояние от ядровой точки, наименее удаленной от растянутой грани, до центра тяжести приведенного сечения: Упругопластический момент сопротивления по растянутой зоне: Где г=1.75 – для тавровых сечений с полкой в сжатой зоне. Упругопластический момент сопротивления по сжатой зоне: Где г=1.5 – для тавровых сечений с полкой в растянутой зоне при bf /b˃2 и hf /h˂0.2. 2.5 Потери предварительного напряжения Потери от релаксации напряжения в арматуре: Потери от температурного перепада у2 =0 (изделие подвергается тепловой обработке вместе с силовой формой). Усилие обжатия с учетом потери у1 : Эксцентриситет этого усилия относительно центра тяжести приведенного сечения: l Напряжение в бетоне при обжатии: Передаточная прочность бетона должна быть не менее: Принимаем Rbp =12 МПа. 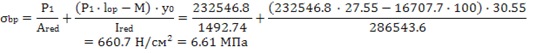 Сжимающее напряжение на уровне центра тяжести напрягаемой арматуры с учетом изгибающего момента от собственного веса плиты и передаточной прочности бетона. Потери от быстро натекающей ползучести: Итого, первые потери: Потери от усадки бетона уb =40 МПа. Усилие обжатия с учетом всех первых потерь: Сжимающее напряжение на уровне центра тяжести растянутой арматуры с учетом изгибающего момента от собственного веса плиты: Потери от ползучести бетона: Вторые потери: Полные потери: Усилия обжатия с учетом всех потерь: 2.6 Расчет продольных ребер плиты по образованию трещин, нормальных к продольной оси элемента Ядровый момент усилия обжатия: Где γsp =1-Δγsp =1-0.13=0.87 – коэффициент натяжения арматуры. Момент образования трещин: Трещины в растянутой зоне в процессе эксплуатации образуются. Необходим расчет по раскрытию трещин. Проверку образования трещин в верхней зоне при ее обжатии проводим из условия: Где Р1 – усилие обжатия с учетом первых потерь; М – изгибающий момент от собственного веса плиты; Rbtp – прочность бетона на растяжение к моменту передачи напряжения, соответствующая передаточной прочности бетона. γsp =1+Δγsp =1+0.13=1.13 Трещины в верхней зоне плиты при ее обжатии не образуются. 2.7 Расчет по раскрытию трещин, нормальных к продольной оси элемента Для изгибаемых элементов, армированных стержневой арматурой, ширина раскрытия трещин определяется по формуле: Где ц1 при длительном действии нагрузки – 1.4, при кратковременном – 1; ц2 =0.5 для арматуры периодического профиля; ц3 =1 для изгибаемых элементов; уs – напряжение в продольной растянутой арматуре, определяемое по формуле: Где М – момент от нагрузок, учитываемых в расчете; zs – расстояние от центра тяжести растянутой арматуры до точки приложения равнодействующей усилий в сжатой зоне элемента. Для элементов тавровой формы значение zs может быть принято равным: ls – базовое расстояние между смежными нормальными трещинами: Значение lb должно быть не менее 10 см и не более 40 см. Принимаем lb =40 см. Где Аbt – площадь сечения растянутой зоны бетона. шs – коэффициент, учитывающий неравномерное распределение относительных деформаций растянутой арматуры между трещинами: Непродолжительная ширина раскрытия трещин: Где аcrc 1 – ширина раскрытия трещин от продолжительного действия постоянной и временной длительной нагрузок; аcrc 2 – от непродолжительного действия постоянных и временных (длительных и кратковременных) нагрузок; аcrc 3 – от непродолжительного действия постоянных и временных длительных нагрузок. Допустимая ширина раскрытия трещин 0.3 мм – непродолжительная и 0.2 мм – продолжительная. 2.8 Расчет прогиба плиты плита трещина арматура ригель Так как деформации плиты ограничиваются эстетическими соображениями, расчет прогиба плиты проводим на действие постоянных и длительных нагрузок. Эксцентриситет продольной силы: Где Ntot =P2 =167242.1 Н. Коэффициент, характеризующий неравномерность деформации растянутой арматуры: 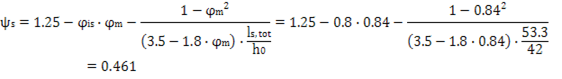 Плечо внутренней пары сил Z1 =39.5 см. Величина площади сжатой зоны бетона: Кривизна оси при изгибе: 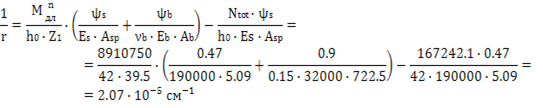 Прогиб от действия длительной и постоянной нагрузок: Допустимый прогиб равен 2.5 см. Прогиб плиты от действия длительной и постоянной нагрузок менее допустимого. 3. Расчет неразрезного железобетонного ригеля Бетон ригеля тяжелый класса В20. Рабочая продольная и поперечная арматура без предварительного напряжения класса А-400. Пролет среднего ригеля принимаем равным расстоянию между гранями колонн 5.65 м (рис. 5), пролет крайнего ригеля равным расстоянию от грани колонны до центр опоры на стене 5.6 м (рис. 5). Сечение колонн принимаем 40*40 см, заделку ригеля в стену – 30 см, центра опоры посередине опорной площадки. Расчетный ригель – средний. 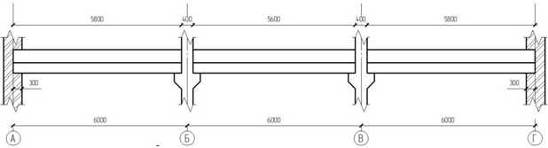 Рисунок 5 3.1 Определение нагрузки на ригель Определяем нагрузку от собственного веса ригеля: Где Ар =0.3625 м2 – площадь сечения ригеля; с – объемная масса железобетона; гf – коэффициент надежности по нагрузке. Нагрузка на ригель: Постоянная нагрузка на 1 м ригеля: Временная нагрузка на 1 м ригеля: Суммарная нагрузка: 3.2 Статический расчет ригеля Изгибающие моменты в сечениях ригеля: Где β – коэффициент, зависящий от Vриг /qриг и от положения сечения. Изгибающие моменты определяем с учетом пластического перераспределения моментов. Разбиваем пролеты на пять равных частей и определяем изгибающие моменты через 1/5 пролета. По результатам расчета строим объемлющие эпюры изгибающих моментов для первого (крайнего) и второго (среднего) пролетов. Эпюры приведены на рис. 6. 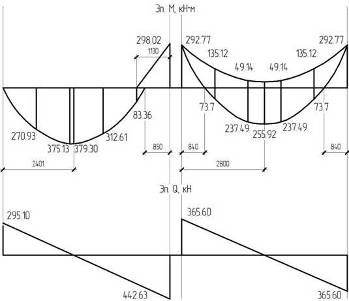 Рисунок 6. – Эпюры изгибающих моментов и поперечных сил крайнего и среднего ригеля Изгибающие моменты в первом пролете: Расстояние от грани колонны до нулевой точки верхней ветви эпюры: Расстояние от грани колонны до нулевой точки нижней ветви эпюры: Поперечная сила на крайней опоре: Поперечная сила на первой промежуточной опоре слева: Изгибающие моменты во втором пролете: Расстояние от грани колонны до нулевой точки нижней ветви эпюры: Поперечная сила на левой и правой опорах среднего пролета: |
