Устройства СВЧ и Антенны. 1. Классификация направляющих систем

• Название: 1. Классификация направляющих систем
• Анкор: Устройства СВЧ и Антенны
• Дата: 18.04.2022
• Размер: 0.54 Mb.
• Имя файла: sekretnaya_informatsia.docx
• Тип: Документы; #481625
• страница: 2 из 7

Активная мощность

Среднее за период T значение мгновенной мощности называется активной мощностью: P= 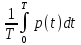. В цепях однофазного синусоидального тока P=U x I x cosφ, где U и I — действующие значения напряжения и тока, φ — угол сдвига фаз между ними. Для цепей несинусоидального тока электрическая мощность равна сумме соответствующих средних мощностей отдельных гармоник. Активная мощность характеризует скорость необратимого превращения электрической энергии в другие виды энергии (тепловую и электромагнитную). Активная мощность может быть также выражена через силу тока, напряжение и активную составляющую сопротивления цепи r или её проводимость g по формуле P=I² x r=U² x g. В любой электрической цепи как синусоидального, так и несинусоидального тока активная мощность всей цепи равна сумме активных мощностей отдельных частей цепи, для трёхфазных цепей электрическая мощность определяется как сумма мощностей отдельных фаз. С полной мощностью S активная связана соотношением P=S x cosφ. Единица активной мощности — ватт (W, Вт).

В теории длинных линий (анализ электромагнитных процессов в линии передачи, длина которой сравнима с длиной электромагнитной волны) полным аналогом активной мощности является проходящая мощность, которая определяется как разность между падающей мощностью и отраженной мощностью.

Реактивная мощность

Реактивная мощность — величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи синусоидального переменного тока, равна произведению действующих значений напряжения U и тока I, умноженному на синус угла сдвига фаз φ между ними: Q=U x I x sinφ (если ток отстаёт от напряжения, сдвиг фаз считается положительным, если опережает — отрицательным). Единица реактивной мощности — вольт-ампер реактивный (var, вар). Физически "реактивная мощность" - это, например, энергия, затрачиваемая на перемагничивание короткозамкнутой обмотки асинхронного двигателя при его работе, то есть ЛЮБОЙ асинхронный двигатель потребляет реактивную мощность из сети независимо от момента на своем валу. Реактивная мощность связана с полной мощностью S и активной мощностью Р соотношением: |Q| = 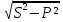. Синхронные генераторы, установленные на электрических станциях, могут как производить, так и потреблять реактивную мощность в зависимости от величины тока возбуждения, протекающего в обмотке ротора генератора. За счет этой особенности синхронных электрических машин осуществляется регулирование заданного уровня напряжения сети. Для устранения перегрузок и повышения коэффициента мощностиэлектрических установок осуществляется компенсация реактивной мощности.

Необходимо отметить, что величина sin φ для значений φ от 0 до плюс 90° является положительной величиной. Величина sin φ для значений φ от 0 до —90° является отрицательной величиной. В соответствии с формулой Q = UI sin φ реактивная мощность может быть как положительной величиной (если нагрузка имеет активно-индуктивный характер), так и отрицательной (если нагрузка имеет активно-ёмкостный характер). Данное обстоятельство подчёркивает тот факт, что реактивная мощность не участвует в работе электрического тока. Отрицательное значение активной мощности нагрузки характеризовало бы нагрузку как генератор энергии. Активное, индуктивное, ёмкостное сопротивление не могут быть источниками постоянной энергии.

Модуль величины Q = UI sin φ приблизительно описывает реальные процессы преобразования энергии в магнитных полях индуктивностей и в электрических полях емкостей.

Применение современных электрических измерительных преобразователей на микропроцессорной технике позволяет производить более точную оценку величины энергии возвращаемой от индуктивной и емкостной нагрузки в источник переменного напряжения.

Измерительные преобразователи реактивной мощности, использующие формулу Q = UI sin φ, более просты и значительно дешевле измерительных преобразователей на микропроцессорной технике.

Cкорость движения электромагнитных волн постоянна, равна скорости света, и определяется относительно самой электромагнитной волны, а не относительно материальных объектов, которых множество. А следовательно скорость одного и того же материального объекта относительно других объектов различная в одно и то же время. По этому электромагнитные волны существуют и двигаются независимо от материи, которая сама является материализованной энергией электромагнитных волн. Это подтверждается тем, что при распаде атомов образуется энергия с исчезновением самих атомов. Также свет от далёких звёзд летит к нам миллионы лет. За это время сама звезда может перестать существовать. А энергия летит. То есть согласно "закона сохранения энергии" энергия не исчезает и не возникает из ничего, а переходит в другое состояние. Например, свет переходит в тепло, что есть ничто иное, как увеличение скорости обращения энергии в самом веществе, на которое попал свет. В том числе из энергии формируется материя в виде её квантов. Если материя излучает энергию (у каждого материального объекта свой спектр), то это говорит о том, что эта материя состоит из энергии. 

5. Плоские однородные волны. Коэффициент ослабления коэффициент фазы.

Одной из важнейших характеристик волн является вид поверхностей равных фаз, т. е. поверхностей, у которых в данный момент времени фазы в любой точке одинаковы. Эти поверхности называют фронтом волны.
Форма фазовой поверхности зависит от условий возникновения и распространения волн. У плоских волн поверхности равных фаз представляют собой плоскости. Гармоническая волна, описываемая уравнением, где A, k, ω — постоянные, является бегущей волной: во всех точках плоскости z = const значения амплитуд и фаз одинаковы. Плоские волны, у которых плоскости равных амплитуд и фаз совпадают, называются однородными плоскими волнами.
Можно легко показать, что при некоторых определенных условиях в плоской гармонической волне плоскости равных амплитуд и фаз могут не совпадать. Такие волны называются неоднородными плоскими волнами. Они играют большую роль при полном отражении. Возникают неоднородные плоские волны при распространении в сложных оптических системах и неоднородных средах. В настоящее время вопросы, связанные с поведением неоднородных плоских волн, весьма актуальны в связи с развитием интегральной и планарной оптики. Не задаваясь пока вопросами возникновения и поведения таких волн, выясним принципиальную возможность их существования.

Плоские электромагнитные волны в однородной

изотропной среде

→

Плоской называется электромагнитная волна, векторы E и

→

H которой имеют постоянные фазы на плоскости, ортогональной

направлению распространения. Эта плоскость называется фронтом

волны, ее называют еще поверхностью равных фаз или волновой

поверхностью или синфазной поверхностью. Плоская волна

→ →

называется однородной, если амплитуды векторов E и H не

меняются в плоскости фронта. Возбудить в неограниченном

пространстве плоскую однородную волну с помощью реального

устройства невозможно, так как при этом источник должен

представлять бесконечную синфазную плоскость и затрачивать

бесконечную мощность. Понятие плоской однородной волны

применяется как простейшая математическая модель,

раскрывающая основные свойства свободных электромагнитных

волн. В реальных случаях это понятие используется при

аппроксимации сложного волнового фронта в локальных условиях

пространства. Так на достаточно большом расстоянии от источника

малый участок сферического фронта в ограниченных участках

пространства из-за малой кривизны можно заменить плоскостью и

сферическую волну локально аппроксимировать плоской волной.

Например, пусть сферическая волна создается элементарным

электрическим вибратором. Рассмотрим электромагнитное поле в

дальней зоне в безграничной однородной изотропной среде без

→ →

потерь. Предположим, что векторы поля E и H требуется знать

только в области V, размеры которой малы по сравнению с

расстоянием до источника r0. Под объемом V можно понимать

объем приемной антенны с поперечными размерами малыми по

сравнению с расстоянием до излучателя. Введем декартову систему

координат x, y, z, ось z которой проведена вдоль радиуса – вектора,

соединяющего середину вибратора Q с точкой O, принятой за

начало координат.
Коэффициент ослабления отраженной волны рассчитывается по формуле:

K=B*2*L

где K — коэффициент ослабления отраженной волны; В - удельное затухание, дБ/м; L - длина кабеля, м.

В этой формуле коэффициент 2 учитывает тот факт, что сигнал испытывает ослабление при передаче от источника СВЧ сигнала к антенне и на обратном пути. Так как при использовании кабеля PK50-7-15 удельное затухание на частотах Си-Би (около 27 МГц) составляет 0,04 дБ/м, то при длине кабеля 40 м отраженный сигнал будет испытывать затухание 0,04*2*40=3,2 дБ. Это приведет к тому, что при реальном значении КСВН, равном 2,0, прибор покажет только 1,38; при реальном значении 3,0 прибор покажет около 2,08.
коэффициент фазы.

Коэффициент фазы 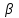характеризует изменение фазы волны или напряжения при распространении электромагнитной волны вдоль линии, является погонным параметром, измеряется в радианах (рад/км) или градусах (град/км), определяется из (4.18):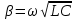

(4.22)

Скорость распространения энергии по цепям связи. Электромагнитная энергия распространяется по цепям связи с определенной скоростью и зависит от первичных параметров линии, определяется выражением .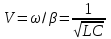

Таким образом, затухание цепи определяет качество и дальность связи, а коэффициент фазы – скорость движения энергии вдоль линии.

Кроме скорости распространения энергии при анализе используются понятия фазовой и групповой скоростей. Фазовая скорость определяет скорость движения поверхности равных фаз в НС (или скорость движения волнового фронта); групповая скорость при передаче сигналов определяет скорость распространения максимума огибающей группы составляющих сложного сигнала, т.е. она характеризует скорость распространения группы волн.

6. Бегущие и стоячие волны. Прямая и обратная волны.

Бегущая волна — волновое движение, при котором поверхность равных фаз (фазовые волновые фронты) перемещается с конечной скоростью (постоянной для однородной среды). С бегущей волной, групповая скорость которой отлична от нуля, связан перенос энергии, импульса или других характеристик процесса^[1].

Бегущая волна - волна, которая при распространении в среде переносит энергию (в отличие от стоячей волны). Примеры: упругая волна в стержне, столбе газа, жидкости, электромагнитная волна вдоль длинной линии, в волноводе^[2].

Бегущая волна — волновое возмущение, изменяющееся во времени  и пространстве  согласно выражению

y(z,t) = A(z,t)sin(kz-wt+φ)

где A(z,t) — амплитудная огибающая волны, k — волновое число и φ — фаза колебаний. Фазовая скорость 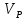  этой волны даётся выражением

=

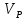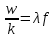где 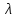  — это длина волны.

Частные случаи.

Стоячая волна является частным случаем бегущей волны с 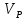 =0.

То есть, две одинаковые периодические бегущие волны (в рамках справедливости принципа суперпозиции), распространяющиеся в противоположных направлениях, образуют стоячую волну.

Частично бегущая волна.

Возникает при разных амплитудах.