Устройства СВЧ и Антенны. 1. Классификация направляющих систем
 Скачать 0.54 Mb.
|
2. Классификация направляемых волн Направляемые электромагнитные волны классифицируют в зависимости от присутствия в них продольных и поперечных составляющих поля. Как правило, за направление распространения волны выбирают ось z. Все направляемые волны классифицируют на следующие типы: 1) ТЕМ волны или поперечные электромагнитные волны. Такие волны также обозначают ТМ, Т. К ним относятся плоские волны, свободно распространяющиеся в неограниченном пространстве. Ориентация векторов , , образует правую тройку векторов. В качестве примера на рис. 4.5 приведены некоторые варианты структуры ТЕМ волны при распространении в свободном пространстве. Учтем связь между , , , которая выражается формулой 2) Н-тип волны, или ТЕ-волна (поперечно электрическая). Такие волны содержат и продольные и поперечные составляющие магнитного Н-поля, электрическое поле имеет только перпендикулярную составляющую (). 3) Е-тип волны, или ТН-волна (поперечно магнитная). Такие волны содержат одновременно и продольные и поперечные составляющие электрического поля, магнитное поле имеет только поперечную составляющую (). 4) Гибридные, или смешанные волны. Такие волны одновременно содержат обе продольные составляющие и. На границе раздела двух сред в любой направляющей системе выполняются граничные условия. Ранее мы рассмотрели распространение радиоволн вдоль одной проводящей поверхности. Для увеличения степени локализации энергии электромагнитной волны можно поставить вторую проводящую плоскость, параллельную первой. Система, состоящая из двух параллельных плоскостей, будет действовать, т.е. электромагнитная волна будет распространяться в пространстве между плоскостями, если на каждой границе раздела будут выполняться граничные условия. Иными словами, и на верхней, и на нижней плоскости должно выполняться условие . 3. Энергия и мощность ЭМВ. Теорема Умова-Пойтинга. Энергия электромагнитных волн Как показывает опыт, электромагнитные волны могут производить различные действия: нагревание тел при поглощении света, вырывание электронов с поверхности металла под действием света (фотоэффект). Это свидетельствует о том, что электромагнитные волны переносят энергию. Эта энергия заключена в распространяющихся в пространстве электрическом и магнитном полях. Теорема умова-пойтинга. Энергетические соотношения для электромагнитного поля Рассмотрим баланс энергии электромагнитного поля. Запас энергии в объеме определяется суммой электрической и магнитной энергии: 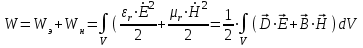 (4.5)где первое слагаемое – энергия электрического поля, а второе – магнитного. Это выражение аналогично известной формуле для колебательного контура: 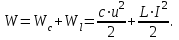 Используя выражение Максвелла можно получить выражение: 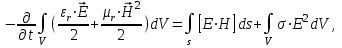 (4.6)где ds– элемент поверхности, ограничивающий объем V. Это выражение известно как теорема Умова-Пойтинга. Левая часть выражения характеризует расход электромагнитной энергии в единицу времени. Первое слагаемое правой части представляет поток энергии в единицу времени через замкнутую поверхность S объема Vв окружающее пространство. Энергия, распространяющаяся в единицу времени через поверхность, перпендикулярную направлению потока энергии, определяется величиной 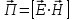 называется вектором Пойнтинга. Второе слогаемое определяет энергию внутри объема, которая преобразовалась в тепло.Изменение запаса энергии, находящейся в некотором объеме V, происходит за счет расхода энергии внутри объема и распространения ее за пределы этого объема. Теорема Умова-Пойнтинга устанавливает связь между напряженностями полей Е и Н на поверхности какого-либо объема с потоком энергии, входящей в объем или выходящей из него. Зная величины Е и Н на поверхности НС можно определить поглощаемую и распространяющуюся электромагнитную энергию. 4. Вектор Пойтинга. Активная и реактивная мощность ЭМП. Скорость движения ЭМВ. Вектор Пойнтинга (также вектор Умова — Пойнтинга) — вектор плотности потока энергии электромагнитного поля, одна из компонент тензора энергии-импульса электромагнитного поля. 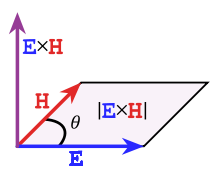 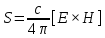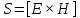Вектор Пойнтинга S можно определить через векторное произведениедвух векторов:  (в системе СГС), (в системе СИ),где E и H — вектора напряжённости электрического и магнитного полей соответственно. 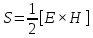 (в комплексной форме),где E и H — вектора комплексной амплитуды электрического и магнитного полей соответственно. Этот вектор по модулю равен количеству энергии, переносимой через единичную площадь, нормальную к S, в единицу времени. Своим направлением вектор определяет направление переноса энергии. Поскольку тангенциальные к границе раздела двух сред компоненты E и H непрерывны (см. граничные условия), то вектор S непрерывен на границе двух сред. В переменном электрическом поле формула для мощности постоянного тока оказывается неприменимой. На практике наибольшее значение имеет расчёт мощности в цепях переменного синусоидального напряжения и тока. Для того, чтобы связать понятия полной, активной, реактивной мощностей и коэффициента мощности, удобно обратиться к теории комплексных чисел. Можно считать, что мощность в цепи переменного тока выражается комплексным числом таким, что активная мощность является его действительной частью, реактивная мощность — мнимой частью, полная мощность — модулем, а угол φ (сдвиг фаз) — аргументом. Для такой модели оказываются справедливыми все выписанные ниже соотношения. |