Характеристика
Характеризуется или коэффициентом бегучести волны (КБВ), или коэффициентом стоячести волны (KCB), или коэффициентом отражения Г, равным отношению амплитуд встречных волн[1]:
KCB=1/КБВ=(1+|Г|²)/(1-|Г|²)
По линиям передач оптимальная передача энергии требует их согласование: получение в линии режима бегущей волны - KCB=1, Г=0.
Такой режим для цепей с сосредоточенными параметрами будет соответствовать равенству внутреннего сопротивления источника сопротивлению нагрузки.
Стоя́чая волна́ — колебания в распределённых колебательных системах с характерным расположением чередующихся максимумов (пучностей) и минимумов (узлов) амплитуды. Практически такая волна возникает при отражениях от преград и неоднородностей в результате наложения отражённой волны на падающую. При этом крайне важное значение имеет частота, фаза и коэффициент затухания волны в месте отражения.
Примерами стоячей волны могут служить колебания струны, колебания воздуха в органной трубе[1]; в природе — волны Шумана.
Чисто стоячая волна, строго говоря, может существовать только при отсутствии потерь в среде[2] и полном отражении волн от границы. Обычно, кроме стоячих волн, в среде присутствуют и бегущие волны, подводящие энергию к местам её поглощения или излучения.
Для демонстрации стоячих волн в газе используют трубу Рубенса.
ОБРАТНАЯ ВОЛНА - волна с противоположно направленными фазовой и групповой скоростями. Впервые термин "О. в." введён в ВЧ-электронике, где на взаимодействии О. в. с электронными пучками основано действие широкого класса СВЧ-приборов - ламп обратной волны. Волны с подобными свойствами известны также в пространственно-периодич. структурах и средах.
Простейшими примерами О. в. являются системы с плоскими волнами, в частности в линиях передачи, где распространение волн возможно только вдоль к--л. определённого направления.
7. Телеграфные уравнения. Волновые уравнения для тока и напряжения.
Телеграфные уравнения — пара линейных дифференциальных уравнений, описывающих распределение напряжения и тока в линии электропередачи по времени и расстоянию. Уравнения были составлены Оливером Хевисайдом, в 1880-х разработавшим модель линии электропередачи, описанную в этой статье. Теория Хевисайда применима к линиям электропередачи всех частот, включая высокочастотные линии (такие, как телеграфные и радиочастотные проводники), линии со звуковыми частотами (например, телефонные линии), низкочастотные линии (например, силовые линии) и постоянный ток.
Телеграфные уравнения, как и все другие уравнения, описывающие электрические явления, могут быть сведены к частному случаюуравнений Максвелла. С точки зрения практики, предполагается, что проводники состоят из бесконечной цепи двухполюсников, каждый из которых представляет собой бесконечно короткий участок линии:
Удельное сопротивление проводников R представлено в виде резистора (выражается в Омах на единицу длины).
Удельная индуктивность L (возникает из-за магнитного поля вокруг проводников, самоиндуктивности и т. д.) представлена в видекатушки (генри на единицу длины).
Емкость C между двумя проводниками представлена в виде конденсатора (фарад на единицу длины).
Проводимость диэлектрического материала, разделяющего два проводника (изоляции) G представлена в виде резистора между проводом под напряжением и нулевым проводом (сименс на единицу длины). В модели этот резистор имеет сопротивление 1 / GОм.
Для ясности повторим, что модель основана на бесконечной цепи элементов, показанных на картинке, и номиналы ее частей указанына единицу длины. Также можно использовать R', L', C' и G', чтобы подчеркнуть, что значения являются производными по координате.
Телеграфные уравнения. Волновые уравнения для напряжения и тока
В линиях передачи Т-волны возможен переход от векторных величин 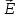 и и 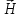 к скалярным величинам U (напряжение между проводниками 1 и 2) и I (ток): к скалярным величинам U (напряжение между проводниками 1 и 2) и I (ток):
 ; ; 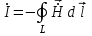 ; (15.1) ; (15.1)
где L – замкнутый контур, охватывающий проводник с током.
Телеграфные уравнения выводятся из уравнений Максвелла (3.16) и (3.17). ЭМП Т-волны имеет только поперечные составляющие, поэтому достаточно определить проекцию ротора на поперечную плоскость S:
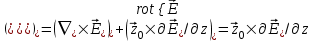 . (15.2) . (15.2)
Следовательно, уравнения Максвелла для Т-волны принимают вид:
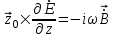 ; ; 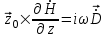 . (15.3) . (15.3)
8. Основные параметры ЭМВ. Поляризация ЭМВ. Длина волны.
Период колебания волны [T] -время, за которое точка радиоволны, имеющая какую-то фиксированную фазу, проходит путь, равный длине волны
Частота колебаний электромагнитного поля [F] -число колебаний поля в секунду F=1/T. Единицей измерения частоты является герц (Гц)
Скорость распространения волны [С] - в свободном пространстве (вакууме) постоянна и равна скорости света С= 300 000 км/с. скорость движения радиоволны зависит от свойств среды, она обычно меньше С на величину коэффициента преломления среды. С=Lв*F. где Lв – длинна волны
Поляризация радиоволн - Поляризацией называется ориентировка вектора электрического поля Е волны относительно поверхности земли.
Горизонтальная поляризация - Радиоволны с горизонтальным вектором электрического поля (Линейная поляризация)
Вертикальная поляризация - Радиоволны с вертикальным вектором электрического поля (Линейная поляризация)
При таких видах поляризации требуется соответствующее расположение передающей и принимающей антенн. Обе горизонтально или вертикально в соответствии с поляризацией. Иначе приема не будет.
Круговая - Для приёма сигнала не важно положение плоскости поляризации передающей и приёмной антенн
круговая поляризация — вещь теоретическая. На практике говорят об антеннах
Плоскостью поляризации называют плоскость, проходящую через на-правление распространения и вектор.
ЭЛЛИПТИЧЕСКОЙ поляризации — с левым или правым направлением вращения вектора E
Длинна волны - расстояние между двумя ближайшими друг к другу точками, колеблющимися в одинаковых фазах
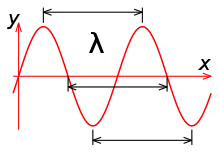
Амплитуда – максимальное значение
Плотность энергии электромагнитного поля может быть выражена через значения электрического и магнитного полей:
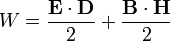
Интенсивность — скалярная физическая величина, количественно характеризующая поток энергии, переносимой волной в некотором направлении. Численно интенсивность равна количеству энергии, переносимому через единичную площадку расположенную перпендикулярно направлению потока энергии, усреднённому за период волны. Интенсивность электромагнитного излучения равна модулю вектора Пойнтинга
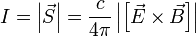
Для монохроматической линейно поляризованной волны с амплитудой напряжённости электрического поля E0 интенсивность равна:
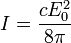
Для циркулярно поляризованной волны это значение в два раза больше:
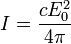
9. Групповая и фазовая скорости. Скорость движения энергии ЭМВ.
Итак, в результате суперпозиции(суммы) нескольких синусоидальных волн образуется несинусоидальная волна с каким-то набором частот и волновых чисел. За скорость распространения такой волны в пространстве берётся скорость распространения фиксированной амплитуды. Но если в случае простой синусоидальной волны эта скорость совпадает со скоростью распространения фиксированной фазы (мы назвали эту скорость фазовой), то в случае сложной несинусоидальной волны сама амплитуда зависит от времени и координат (см. предыдущий пример). Амплитуда сложной волны есть:
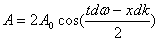
Фиксированная амплитуда А будет удовлетворять условию: 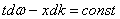
Скорость распространения фиксированной амплитуды в несинусоидальной волне получается следующей:
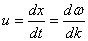 ГРУППОВАЯ СКОРОСТЬ ГРУППОВАЯ СКОРОСТЬ
Эта скорость называется ГРУППОВОЙ СКОРОСТЬЮ волны. Она в общем случае отличается от ФАЗОВОЙ СКОРОСТИ:
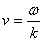 ФАЗОВАЯ СКОРОСТЬ ФАЗОВАЯ СКОРОСТЬ
Связь между этими скоростями можно легко получить (учтя зависимость частоты и волнового числа от длины волны):
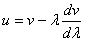
Среда называется ДИСПЕРГИРУЮЩЕЙ, если в ней волны разной длины распространяются с разной скоростью. Зависимость скорости волны (фазовой) от длины волны (или, что то же самое, от частоты) называется ДИСПЕРСИЕЙ.
Видно, что групповая скорость будет совпадать с фазовой только в недиспергирующих средах, где составляющие сложной волны будут перемещаться с одинаковой скоростью, и сама сложная волна не будет менять своей формы (не будет "расплываться").
Для МОНОХРОМАТИЧЕСКОЙ ВОЛНЫ (так называется простая синусоидальная волна, имеющая одну частоту) фазовая и групповая скорости всегда совпадают, даже в диспергирующих средах.
СКОРОСТЬ ДВИЖЕНИЯ ЭМВ возможно совпадает с фазовой. Ответа не нашел!!!!!!
10. Согласование линии передачи с генератором и нагрузкой (общие принципы)
Линия называется идеально согласованной с нагрузкой, если в ней отсутствуют отраженные волны. Однако при передаче по цепи СВЧ сигналов, занимающих определенную полосу частот, обеспечить идеальное согласование линии с нагрузкой во всей требуемой полосе частот практически невозможно. Поэтому при проектировании задают допустимый уровень рассогласования в требуемой полосе частот Δf=f2-f1,Этот уровень определяют величиной Гдоп (Модуль коэффициента отражения изменяется в пределах:
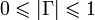
| Г | = 0, если отражения от нагрузки отсутствуют
| Г | = 1, если волна полностью отражается от нагрузки, то есть
или КБВД0П (Коэффициент бегущей волны) так, чтобы при f1≤f≤f2выполнялось соотношение | Г(z) | ≤ Гдоп или КБВ≥КБВДОП. Линии, в которых выполняются эти неравенства, называются согласованными с нагрузкой. Интервал частот Δf называют полосой согласования. Иногда говорят об относительной полосе согласования Δfomн=Δf/f0, где fo = (f1+f2)/2. Эту величину можно вычислять в процентах:
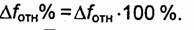
Согласование (в электронике) сводится к правильному выбору сопротивлений генератора (источника), линии передачи и приёмника (нагрузки). Идеального Согласование (в электронике) между линией и нагрузкой можно достичь при равенстве волнового сопротивления линии r полному сопротивлению нагрузки Zh = RH + j ХН, или при RH= r и XH= 0, где RH - активная часть полного сопротивления, XH - его реактивная часть.
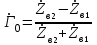 ; ; 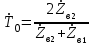 . (13.15) . (13.15)
Из (13.15) следует, что при нормальном падении ЭМВ на границу раздела отраженная волна будет отсутствовать (Г0=0) только в том случае, если волновые сопротивлений сред равны (условие согласования сред).
11. Критерии согласования ЛП с генератором и нагрузкой.
Комплексный коэффициент отражения по напряжению
арактеризует степень согласования линии передачи с нагрузкой. Модуль коэффициента отражения изменяется в пределах: 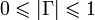
| Г | = 0, если отражения от нагрузки отсутствуют и BU = 0[6];
| Г | = 1, если волна полностью отражается от нагрузки, то есть | AU | = | BU | ;
Коэффициенты бегущей и стоячей волны
По эпюре напряжения судят о степени согласования линии с нагрузкой. Для этого вводятся понятия коэффициента бегущей волны — kБВ и коэффициента стоячей волны kСВ:
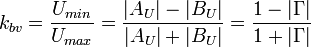
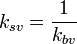
Эти коэффициенты, судя по определению, изменяются в пределах:
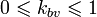 ; ; 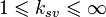
На практике наиболее часто используется понятие коэффициента стоячей волны, так как современные измерительные приборы (панорамные измерители kСВ) на индикаторных устройствах отображают изменение именно этой величины в определенной полосе частот.
Входное сопротивление длинной линии
Входное сопротивление линии — является важной характеристикой, которое определяется в каждом сечении линии как отношение напряжения к току в этом сечении:
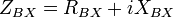
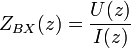
Так как напряжение и ток в линии изменяются от сечения к сечению, то и входное сопротивление линии изменяется относительно ее продольной координаты z. При этом говорят о трансформирующих свойствах линии, а саму линию рассматривают как трансформатор сопротивлений. Подробнее свойство линии трансформировать сопротивления будет рассмотрено ниже.
Режимы работы длинной линии:
Режим бегущей волны
Режим бегущей волны характеризуется наличием только падающей волны, распространяющейся от генератора к нагрузке. Отраженная волна отсутствует. Мощность, переносимая падающей волной, полностью выделяется в нагрузке. В этом режиме BU = 0, | Г | = 0, kбв =kсв = 1[7].
Режим стоячей волны
Режим стоячей волны характеризуется тем, что амплитуда отраженной волны равна амплитуде падающейBU = AU то есть энергия падающей волны полностью отражается от нагрузки и возвращается обратно в генератор. В этом режиме, | Г | = 1, kсв = 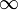 , kбв = 0[7]. , kбв = 0[7].
Режим смешанных волн
В режиме смешанных волн амплитуда отраженной волны удовлетворяет условию 0 < BU < AU то есть часть мощности падающей волны теряется в нагрузке, а остальная часть в виде отраженной волны возвращается обратно в генератор. При этом 0 < | Г | < 1, 1 < kсв < 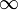 , 0 < kбв < 1 , 0 < kбв < 1
12. Мощность потерь проводимости. Сопротивление проводников на различных частотах.
Мощность тепловых потерь (потерь проводимости) подчиняются закону Дж. Джоуля-Э. Ленца. Изменение запаса энергии имеет размерность мощности:
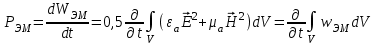 , ,
где WЭМ – энергия ЭМП, а wЭМ – объемная плотность энергии (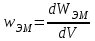 ). ).
Вектор 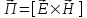 называется вектором Пойтинга. называется вектором Пойтинга.
вектор Пойтинга указывает направление распространения излучения, а его модуль представляет собой плотность потока мощности излучения
энергия ЭМП, превращающаяся в тепло, увеличивается пропорционально частоте и квадрату напряженности электрического поля.
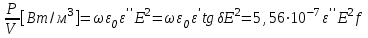
СОПРОТИВЛЕНИЕ В ЗАВИСИМОСТИ ОТ ЧАСТОТЫ
В случае постоянного тока сопротивление проводника цилиндрической формы можно описать формулой (a – радиус проводника):
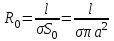
На высоких частотах (при сильном скин-эффекте – эффект уменьшения амплитуды электромагнитных волн по мере их проникновения вглубь проводящей среды. В результате этого эффекта, например, переменный ток высокой частоты при протекании по проводнику распределяется не равномерно по сечению, а преимущественно в поверхностном слое) ЭМП концентрируется в тонком поверхностном слое, что приводит к уменьшению площади сечения проводника (Sэкв = S0 – Sвн), по которой протекает ток и росту сопротивления
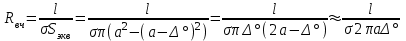 ; ;
где l-длинна. σ – удельная проводимость. S - площадь.
Для расчёта толщины скин-слоя в металле (приближённо) можно использовать следующие эмпирические формулы:
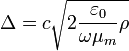 . .
Здесь ε0 = 8,85419×10−12 Ф/м — абсолютная диэлектрическая проницаемость, ρ — удельное сопротивление, c — скорость света, μm — относительная магнитная проницаемость (близка к единице для пара- и диамагнетиков — меди, серебра, и т. п.), 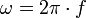 . Все величины выражены в системе СИ. . Все величины выражены в системе СИ.
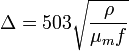
13. Граничные условия для векторов ЭМП. ЭМП на границе раздела с проводником.
Граничные условия для нормальных составляющих векторов электрического поля.
На поверхности идеального проводника есть только нормальные составляющие:
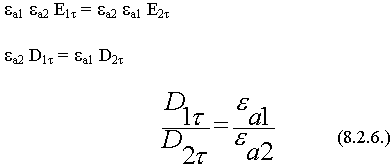
Граничные условия для нормальных составляющих векторов магнитного поля выводятся применением четвертого уравнения Максвелла в интегральной форме (3.4) к элементарному цилиндру (рис. 4.2).
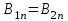 ; ; 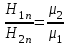 . (4.4) . (4.4)
Таким образом, нормальная составляющая вектора магнитной индукции на границе раздела сред непрерывна, а нормальная составляющая вектора напряженности магнитного поля (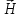 ) претерпевает скачок, равный обратному отношению магнитных проницаемостей сред. ) претерпевает скачок, равный обратному отношению магнитных проницаемостей сред.
14. ЭМП в проводнике. СКИН-ЭФФЕКТ. Локализация ЭМП с помощью проводников.
СКИН-ЭФФЕКТ (поверхностный эффект)
Рассмотрим цилиндрический проводник, по которому течёт ток. Вокруг проводника с током имеется магнитное поле, силовые линии которого являются концентрическими окружностями с центром на оси проводника. В результате увеличения силы тока возрастает индукция магнитного поля, а форма силовых линий при этом остаётся прежней. Поэтому в каждой точке внутри проводника производная 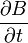 направлена по касательной к линии индукции магнитного поля и, следовательно, линии направлена по касательной к линии индукции магнитного поля и, следовательно, линии 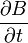 также являются окружностями, совпадающими с линиями индукции магнитного поля. Изменяющееся магнитное поле по закону электромагнитной индукции также являются окружностями, совпадающими с линиями индукции магнитного поля. Изменяющееся магнитное поле по закону электромагнитной индукции
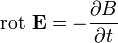
создаёт электрическое индукционное поле, силовые линии которого представляют замкнутые кривые вокруг линии индукции магнитного поля. Вектор напряжённости индукционного поля в более близких к оси проводника областях направлен противоположно вектору напряжённости электрического поля, создающего ток, а в более дальних — совпадает с ним. В результате плотность тока уменьшается в приосевых областях и увеличивается вблизи поверхности проводника, то есть возникает скин-эффект.
Локализация ЭМП с помощью проводников
Рассмотрим механическое действие, которое оказывает ЭМВ на идеально проводящую поверхность. Из граничных условий (9.20) следует, что 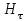 наводит поверхностные токи. наводит поверхностные токи.
С помощью анализа силы, действующей на элемент поверхностного тока в магнитном поле, в [4] выводится формула для вычисления давления, оказываемое на проводник произвольным ЭМП:
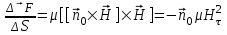
Таким образом, ЭМП оказывает силовое механическое действие, которое аналогично силовому механическому действию вещества.
Из проведенного в разделе анализа можно сделать вывод, что металлические проводники можно использовать для локализации и экранирования ЭМП.
Эффективность экранирования (рост ослабления ЭМП) усиливается с ростом частоты. Улучшить экранирующий эффект можно применением магнитных материалов, магнитная проницаемость которых на рабочей частоте значительно больше единицы (см. Приложение 3).
Для высоких и очень высоких частот целесообразно использовать формулы для сильного скин-эффекта.
17. Потери в диэлектрике и их влияние на характеристики линии передач.
Термин "диэлектрические потери" возник из-за того, что в идеальном диэлектрике энергия может только накапливаться в виде W=0 E 2/2, (на единицу объема, см. (2.1)), но не теряться. В реальном диэлектрике часть энергии уходит из электрической цепи, превращаясь в другой вид энергии, а именно в теплоту. Есть два основных канала превращения энергии в тепло: потери за счет проводимости и поляризационные потери.
Потери за счет проводимости при постоянном напряжении определим из известных выражений. Из закона Ома можно определить мощность, поглощенную веществом изоляции P=U2/Rизол, а из закона Ома в дифференциальной форме (ф-ла (1.23)) следует, что за счет обычной проводимости удельные потери мощности составят Для случая переменного напряжения появляются дополнительные потери, связанные с поляризацией и токами абсорбции, которые принято представлять в виде:
При воздействии переменного напряжения, период которого много меньше времени установления соответствующей поляризации, диэлектрическая проницаемость, соответствующая этому виду не устанавливается и потери, связанные с этим малы. Поэтому в неполярных диэлектриках потери малы, практически на всех частотах. Если период переменного напряжения близок к времени установления поляризации, то потери максимальны.
Следует отметить, что диэлектрические потери в любых материалах зависят от температуры, частоты, влажности, напряженности поля. Частотная зависимость потерь является характеристикой материала и определяется для каждого диэлектрического материала не только свойствами молекул материала, но и наличием и составом примесей. Как правило, потери имеют максимум при одной или нескольких частотах, в зависимости от типа молекул. Положение максимумов характеризуется собственными частотами установления поляризации. Они могут быть связаны с поворотом полярных молекул в жидком диэлектрике или с поворотом домена в сегнетоэлектрике. Например для диэлектрика, соответствующего схеме рис.3б потери максимальны при частоте м
1 / .Исследование частотного поведения потерь, т.н.диэлектрическая спектроскопия позволяет изучать структуру веществ.
Температурная зависимость потерь обычно имеет монотонный характер, потери растут с ростом температуры, хотя у некоторых дипольных диэлектриков наблюдаются локальные максимумы, имеющие ту же природу, что и максимумы в частотной зависимости.
С ростом влажности потери также растут, зачастую весьма значительно. Это связано, как с увеличением сквозной проводимости, так и с поляризацией растворенной и эмульгированной воды.
Увеличение напряженности поля сопровождается ростом tg , что объясняется ростом электропроводности. Причины этого будут подробно рассматриваться в следующем разделе.
18. ЭМВ на границах раздела сред. Полное прохождение и полное отражение. Влияние поляризации на распространение ЭМВ.
ЭМВ на границе раздела сред
ЭМ явления на границе раздела двух разнородных сред (преломление, отражение и т. п.) играют большую роль в теории ЭМП. Границу раздела будем считать плоской и бесконечно протяженной, что позволяет использовать для анализа приближения геометрической оптики и рассматривать ЭМВ в виде лучей. Полученные результаты справедливы и для криволинейных граничных поверхностей и неплоских ЭМВ, если их радиус кривизны значительно больше .
Расположим координатные оси так, чтобы оси y и z лежали в плоскости границы раздела сред (рис. 13.1), а ось x совпадала с направлением вектора нормали (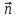 ) для второй среды (2, 2). ) для второй среды (2, 2).
что позволяет сформулировать законы, открытые еще в XVII веке в приближении геометрической оптики В. Снеллиусом и уточненные Р. Декартом [1]:
векторы падающей, отраженной и прошедшей ЭМВ лежат в одной плоскости (плоскости распространения);
угол падения равен углу отражения (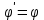 ); );
отношение синусов углов падения и преломления равно отношению комплексных коэффициентов распространения во второй и первой средах (закон преломления В. Снеллиуса):
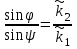 . (13.3) . (13.3)
Коэффициенты отражения и преломления.
Рассмотрим динамические характеристики падающей линейно поляризованной волны на границу раздела двух сред. Интенсивности отраженной и преломленной волн определим через коэффициенты отражения и преломления.
Коэффициентом отражения Г называется отношение комплексных значений напряженностей электрического поля отраженной (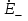 ) и падающей ( ) и падающей (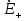 ) волн на границе раздела (х=0). ) волн на границе раздела (х=0).
Коэффициентом прохождения Т во вторую среду из первой называется аналогичное отношение (при x=0) преломленной (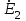 ) и падающей волн ( ) и падающей волн (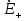 ). ).
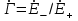 ; ; 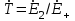 . (13.5) . (13.5)
Значения коэффициентов Г и Т зависят от поляризации падающей волны относительно плоскости падения.
Плоскую однородную ЭМВ, падающую на плоскую поверхность границы раздела двух сред, целесообразно разложить на перпендикулярную и параллельную поляризации. Поэтому ниже будут рассмотрены два случая, в которых плоскость поляризации перпендикулярна и параллельна плоскости падения ЭМВ [11].
|
 Скачать 0.54 Mb.
Скачать 0.54 Mb.