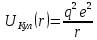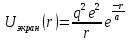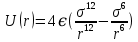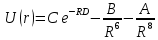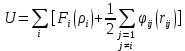Грабовский Д.Е. диплом текст. 1. Кулоновские кристаллы 2 1 История открытия 2
 Скачать 1.58 Mb. Скачать 1.58 Mb.
|
1.5 Применение кулоновских кристаллов1.5.1 Физика твёрдого телаКак было сказано ранее, кулоновские кристаллы представляют собой особый класс твёрдых тел, что делает эти объекты интересными при изучении различных структур и их динамики. Изучение ионных кристаллах в ловушках с периодическим потенциалом позволит осуществить наблюдаемый контролируемый переход между, например, ОЦК и ГЦК6 решётками и наоборот путём изменения только лишь приложенного потенциала. 1.5.2 Физика плазмыПомимо того, что кулоновские кристаллы являются особым видом твёрдых тел, они также представляют собой твёрдое состояние однокомпонентной плазмы. Использование ионных ловушек и удержание в них различных видов ионов позволяет изучать однокомпонентную плазму в различных условиях, наблюдать динамику взаимодействия плазмы из более чем одной компоненты при условиях кулоновской кристаллизации и вдали от неё. 1.5.3 Изучение экзотических космических объектов.Изучение однокомпонентной плазмы в форме полностью ионизированных атомов, как ожидается, сыграет большую роль в понимании процессов, происходящих внутри белых карликов. Такие звёзды состоят в основном из ионов 16O8+ и 12C6+, которые имеют близкие значения соотношения массы и заряда, следовательно, будет интересным проведение экспериментов по взаимодействию такого рода частиц. При проведении экспериментов с сильно заряженными ионами (27Al3+, 36Ar4+, 45Sc5+, 54Fe6+ и др.) показано, что заметную роль в протекании процессов взаимодействия играет тот факт, что кристаллизация для разных сортов частиц происходит при различных температурах. Но требуется ещё много времени, прежде чем такие расчёты могут быть применимы к описанию поведения белых карликов, т.к. модели очень чувствительным к точному определению отношения заряда к массе. 1.5.4 Квантовые вычисленияИз-за существования общих нормальных мод колебаний для частиц, составляющих ионный кристалл, при определённом, точно подобранном воздействии лазерного излучения, из них может быть создана квантово-запутанная система. В работе [22] Сирак (Cirac) и Золлер (Zoller) показали, что универсальные операции квантовых вентилей могут выполняться между любыми двумя кубитами, представленными различными внутренними состояниями ионов. Следовательно, цепочку из N ионов можно использовать в качестве квантового регистра N кубитов в квантовом компьютере. 1.5.5 Квантовые симуляцииВозможность выполнения универсальных вентилей между любыми парами состояний ионных кубитов, позволяет проводить имитацию квантовой динамики любого оператора Гамильтона, действующего на квантовую систему в Гильбертовом пространстве 2N[23]. Хотя такие симуляции могут быть выполнены и на классических компьютерах, размерность пространства увеличивается экспоненциально с увеличением количества задействованных кубитов и в конечном итоге задача становится трудноразрешимой. Изучение магнитного или в более общем случае спин-спинового взаимодействия может быть смоделирована путём имитации двух состояний магнитного диполя или спина двумя внутренними состояниями ионов [24-26]. 2. Расчёт по методу молекулярной динамики2.1 О методе МД Компьютерная молекулярная динамика является одним из наиболее мощных вычислительных методов, эффективно применяемых для моделирования физических и биологических систем. Методы МД позволяют вычислять траектории отдельных атомов и полимерных цепей, исследовать динамику взаимодействия частиц в конденсированных средах на молекулярном уровне. Метод молекулярной динамики обладает высоким пространственным разрешением и позволяет получить информацию о процессах, происходящих в атомно-молекулярных масштабах и на временах порядка нескольких наносекунд [27]. Уровень развития вычислительной техники на сегодняшний день позволяет моделировать динамику молекулярных и атомарных систем, состоящих из тысяч и миллионов частиц, с большим набором параметров, определяющих состояние системы. Широко применяются технологии параллельных вычислений на центральных процессорах и видеокартах, в частности использования языка CUDA для видеокарт производства компании Nvidia. Основой и центральным звеном расчёта методом молекулярной динамики является определение характера и степени взаимодействия взаимно парных частиц в рассматриваемой системе. Такое взаимодействие определяется выбранным потенциалом взаимодействия, который и определяет процессы, происходящие в системе. От выбора потенциала, адекватного модели и физическому процессу, зависит корректность результатов, полученных по итогам расчётов. В таблице 1 приведены некоторые наиболее часто употребляемые потенциалы взаимодействия для газов, жидкостей и твёрдых частиц. Таблица 1 Потенциалы межчастичного взаимодействия
|