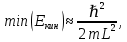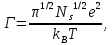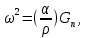Грабовский Д.Е. диплом текст. 1. Кулоновские кристаллы 2 1 История открытия 2

• Название: 1. Кулоновские кристаллы 2 1 История открытия 2
• Дата: 27.05.2022
• Размер: 1.58 Mb.
• Имя файла: Грабовский Д.Е. диплом текст.docx
• Тип: Документы; #553377
• страница: 1 из 6

Содержание

1. Кулоновские кристаллы 2

1.1 История открытия 2

1.2 Кулоновские кристаллы в природе 6

1.3 Получение кулоновских кристаллов в лаборатории 7

1.3.1 Лазерное охлаждение ионов 8

1.3.2 Ионные ловушки 10

1.4 Применение математического моделирования для описания кулоновских кристаллов 12

1.4.1 Методы математического моделирования 13

1.5 Применение кулоновских кристаллов 20

1.5.1 Физика твёрдого тела 20

1.5.2 Физика плазмы 20

1.5.3 Изучение экзотических космических объектов. 20

1.5.4 Квантовые вычисления 21

1.5.5 Квантовые симуляции 21

2. Расчёт по методу молекулярной динамики 22

2.2 Потенциалы взаимодействия 23

2.3 Методы интегрирования уравнения движения 24

2.4 Виды граничных условий 26

3. О результатах работы 29

ВЫВОДЫ ПО ПРОДЕЛАННОЙ РАБОТЕ 34

Список литературы 35

1. Кулоновские кристаллы

1.1 История открытия

Моя работа посвящена изучению особого рода упорядоченных микроструктур, называемых «кулоновскими кристаллами». Кулоновские кристаллы образуются, в отличие от обычных твёрдых веществ, не из-за квантово-механических эффектов, а благодаря классическому механизму электромагнитного взаимодействия между заряженными частицами. В большинстве случаев, кулоновскими кристаллами называют структуры, состоящие из некоторого числа однородных или неоднородных ионов, реже электронов, имеющих крайне низкую температуру. Впервые подобные структуры были предсказаны Юджином Вигнером (Wigner Jenő Pál) в 1934 году. В работе [1] Вигнер теоретически показал, что при крайне низких температурах электроны, если расстояние между ними больше боровского радиуса¹, формируют упорядоченную кристаллическую структуру и совершают малые колебания вблизи положений равновесия. В такой конфигурации потенциальная энергия электронов E_пот значительно меньше кинетической энергии E_кин. Следуя соотношению неопределённости Гейзенберга, кинетическую энергию нельзя положить равной нулю. Поэтому её минимальное значение определяется неравенством

(1)

где m – эффективная масса электрона, ℏ – постоянная Дирака, L – расстояние между электронами. Согласно расчётам Вигнера, электронный кристалл наиболее устойчив при L = 37,5 a₀, где a₀ – боровский радиус.

Хоть вигнеровский кристалл и был предсказан еще в начале 30-х годов XX века, получение такой структуры на практике ещё десятки лет было неосуществимой задачей. Только в 1990 году американскими учёными Граймсом (Grimes) и Адамсом (Adams) [2] удалось получить экспериментальное подтверждение существования электронных кристаллов. Им удалось осуществить процесс фазового перехода от электронной жидкости к электронному кристаллу. Объектом изучения являлась классическая двумерная, 2D, Кулоновская система, состоящая из электронного монослоя, удерживаемого над поверхностью жидкого гелия. Такой электронный слой представляет собой практически идеальную кулоновскую систему, поскольку поверхностная плотность электронов может варьироваться на несколько порядков, а поверхность гелия не имеет удерживающих ловушек и центров рассеяния.

В 1934 году Вигнер [1] показал, что переход электронной жидкости в твёрдую фазу должен происходить в трёхмерной Ферми-система при низких плотностях. Крандал (Crandall) и Уильямс (Williams) [3] вычислили, что аналогичный переход должен происходить и в классической двумерной электронной системе при высокой поверхностной плотности электронов.

Состояние кулоновской электронной системы определяется параметром Г, называемым параметром связи плазмы. Параметр Г есть отношение потенциальной энергии кулоновского взаимодействия E_Кул к кинетической энергии взаимодействующих электронов E_кин. Для классической электронной 2D системы отношение определяется так:

(2)

где N_s – поверхностная плотность электронов, e – элементарный электрический заряд, k_B – постоянная Больцмана, T – температура системы. При Г <1 кинетическая энергия преобладает, и система ведёт себя как электронный газ, при среднем показателе 1 ≤ Г ≤ 100 движение электронов более взаимосвязано и система становится похожа на жидкость. При высоких значениях параметра Г, т. е. при Г ≥ 100, потенциальная энергия кулоновского взаимодействия становиться значительно больше кинетической энергии движения электронов, и система претерпевает фазовый переход в состояние упорядоченного периодического кристаллического массива.

Свободные электроны удерживаются над поверхностью жидкости благодаря совокупному воздействию классического дальнодействующего потенциала и короткодействующего барьера, препятствующего прохождению внутрь жидкости. В такой конфигурации, электроны могут свободно перемещаться только вдоль поверхности жидкого гелия. Значение поверхностной плотности электронов варьировалось от 10⁵ до 10⁹ см^-2, температура составляла примерно 0,5 К, а параметр Г, находился, соответственно, в пределах между 2 и 200 единиц. При плотности электронов N_s= 10⁹ энергия Ферми равна 0,03 К, что мало по сравнению с экспериментальной температурой, поэтому можно считать, что электроны подчиняются классической больцмановской статистике.

Для установления наличия электронного кристалла над поверхностью жидкого гелия был использован подход, предложенный Шикиным (Shikin) и Монархой (Monarkha) в [4, 5]. Шикин предположил, что электронный кристалл под воздействием перпендикулярного высокочастотного электрического поля будет колебаться вверх-вниз над поверхностью жидкого гелия и возбуждать в нём стоячие капиллярные волны – рипплоны. Стоячие капиллярные волны будут резонансно возбуждены, когда целое число длин волн будет укладываться между рядами электронов, а частота возбуждения будет совпадать с частотой капиллярных волн для этой длины волны. Таким образом, резонанс будет возникать, если частота возбуждения удовлетворяет соотношению

(3)

где α – коэффициент поверхностного натяжения, ρ – плотность жидкости, G_n – вектор обратной решётки для электронной решётки. Сами авторы полагали, что обнаружили не моды, описанные Шикиным, а скорее сочетание плазмон-рипплонных мод [6], связанных с неоднородным горизонтальным движением электронов. Плазмон-рипплонные моды имеют гораздо большую поглощающую способность и резонансы на частотах, значительно отличающихся от рассчитанных в [4, 5].

Экспериментальная ячейка состояла из пары круглых пластин конденсатора диаметром 5 см, одна из которых располагалась на расстоянии 0,2 см от поверхности жидкого гелия и содержала нить накала в центре. Вторая пластина была погружена в гелий на глубину 0,1 см. В центре пластины находился радиочастотный элемент, окружённый предохранительным кольцом. Обе пластины были окружены ограничивающим кольцом на поверхности гелия. Ячейка охлаждалась жидким гелием ³He.

Целью эксперимента было обнаружение резонансных частот, соответствующих кристаллизации электронов, при увеличении параметра Г в результате изменения температуры T и поверхностной плотности N_s. Поверхностная плотность электронов N_sпретерпевала изменения в узких пределах под воздействием потенциала, накладываемого на экспериментальную ячейку. Результат эксперимента представлен на рисунке 1, где – отношение действительной части сопротивления электронной структуры к поверхностной плотности электронов, F – частота подаваемого напряжения.



Рисунок 1 – Экспериментальные кривые, подтверждающие наличие кристаллических электронных структур

Кривые на рисунке 1 построены при фиксированном значении электронной плотности N_s= (4,4 ± 0,4) ·10⁸ см² и разных температурах. Резонансы наблюдаются только при температурах ниже 0,457 К, когда электроны должны формировать кристаллическую решётку. Кроме того, определено, что переход электронной структуры из твёрдого состояния в жидкое происходит при температуре, пропорциональной N_s^1/2 и значениях параметра Г = 137±15. Первый компьютерный эксперимент, связанный с моделированием плавления электронного кристалла методом молекулярной динамики показал, что процесс фазового перехода из твёрдого состояния в жидкое начинается при Г = 95 [7]. Последние, к тому времени, вычисления по методу Монте-Карло дали значение параметра Г в пределах от 110 до 140 единиц.