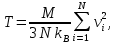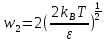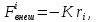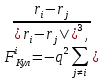Грабовский Д.Е. диплом текст. 1. Кулоновские кристаллы 2 1 История открытия 2
 Скачать 1.58 Mb. Скачать 1.58 Mb.
|
1.4 Применение математического моделирования для описания кулоновских кристалловСоздание в лаборатории условий, необходимых для образования кулоновских кристаллов весьма дорогостоящий процесс, т.к. необходимо наличие, как минимум: ионной пушки; ионной ловушки; лазера, способного охладить ионы до достаточно низких температур; надёжной системы высокого вакуума. Как минимум по этим причинам и, безусловно, в связи с быстрым развитием вычислительных технологий, изучение таких экзотических структур, как ионные кристаллы, проводится на основе математических моделей и компьютерных вычислений. 1.4.1 Методы математического моделированияМетоды математического моделирования применяются в самом широком спектре направлений научных исследований, в частности для моделирования процессов взаимодействия микрочастиц, процессов распыления и напыления тонких плёнок, процессов образования белков, аминокислот и других химических соединений. В настоящее время существует два главных подхода к решению таких задач: использование метода Монте-Карло; использование метода Молекулярной динамики. Метод Монте-Карло – численный метод, основанный на решении задач с использованием случайных величин и последующего вычисления характеристик случайного процесса и их распределений. Он широко применяется в решении как физических и математических задач, так и в финансово – экономической области. Применительно к физике, метод Монте-Карло позволяет, в отличие от классических методов, вычислять необходимые характеристики процесса, не прибегая к макроскопическим величинам [17]. Преимуществом метода является относительная простота его реализации и механизмов, на которых он основан. Каждый раз мы просто моделируем некоторую цепочку процессов, зависимых или нет, применяя генератор случайных чисел и на полученном массиве данных определяем средние характеристики величин и их дисперсию. К недостаткам метода можно отнести довольно низкую точность его оригинального исполнения, зачастую имеет место погрешность результата в 10-15%. Но в настоящее время обычно говорят о Методах Монте-Карло, как о целом семействе методов, с разным подходом к определению случайных величин и, как следствие, снижению погрешности. Метод Молекулярной динамики (МД) возник в молекулярной физике, где получил своё развитие и обоснование. Метод основан на решении уравнения движения второго закона Ньютона для самого широкого спектра взаимодействий двух и более частиц. В зависимости от модели и свойств исследуемого вещества или процесса применяются различные потенциалы, среди которых самые популярные: кулоновский потенциал, потенциал Леннарда-Джонса, потенциал погружённого тела. Классическая задача для метода молекулярной динамики – задача о взаимодействии двух тел. Такая задача вполне может быть решена и аналитически, но добавление к системе ещё хотя бы одной частицы, приводит к практически непреодолимым для аналитического решения трудностям. Численное моделирование методом МД, в свою очередь, позволяет рассчитывать взаимодействие сразу сотен частиц. Впервые метод Молекулярной динамики был описан в статье [18] за авторством Адлера (Adler) и Вэйнрайта (Wainwright), вышедшей в свет в 1957 году. Авторами был проведён расчёт по методу МД для изучения процесса взаимодействия твёрдых сфер, имеющих потенциал притяжения формы 1/r2. На первом этапе расчёта моделировалось взаимодействие частиц в прямоугольной ячейке с периодическими граничными условиями. Изначально, частицы находились в упорядоченной решётке, в качестве начальных параметров задавались: одинаковая для всех частиц начальная скорость; случайное направление скорости частицы. Расчёты проводились для систем, состоящих из 32, 96, 108, 256 и 500 частиц на вычислительных машинах UNIVAC и IBM-704. ЭВМ UNIVAC позволяла обрабатывать до 300 столкновений в час, а IBM-704 вплоть до 7000 столкновений в час для системы из 32 частиц. После запуска система очень быстро достигала Максвелловского распределения скоростей, исходя из чего определялось давления в системе. В работе [19] представлены результаты этих расчётов в сравнении с моделирование методом Монте-Карло, проведённым ранее. Расчёты показали, что при одном и том же значении отношения v/v0, где v– объём, занимаемый частицами, v0 – объём системы, в расчётной ячейке может быть значительно отличающееся давление. Для определения значений v/v0, при которых происходил переход от одного значения давления к другому, производилось моделирование взаимодействия различного количества частиц с определённым заданным количеством столкновений. Было показано, что самая низкая плотность частиц, при которой в системе стабильно сохраняется более низкое давление, составляет v/v0 = 1,5. Определение количества столкновений, необходимого для возникновения флуктуации, достаточно для перехода к более высокому уровню давления, оказалось весьма затруднительным. Даже при разнице v/v0 между двумя экспериментами порядка 0,1, количество столкновений для образования флуктуаций может отличаться в десятки раз. Для определения причин таких сильных расхождений в результатах решения при малейших отклонениях требовало наличие больших вычислительных мощностей, чем имелись у авторов на тот момент. В работе [20] исследовалось поведение кристаллов меди в процессах радиационных повреждений. Медь была выбрана в качестве расчётного материала, потому что к тому времени, 1960 год, она была наиболее распространённым металлом, для которого проводились эксперименты по радиационным повреждениям. Для учёта поведения атомов в процессе передачи энергии внутри кристалла, целесообразно было бы учесть влияние конечной температуры на образец, но авторами принято решение не усложнять процесс вычислений. Кроме того, большинство эффектов, связанных с влиянием температуры, могут быть хорошо предсказаны аналитически. Исходя из этого, все расчёты проводились при температуре абсолютного нуля. Другое значимое ограничение – довольно скромные вычислительные мощности ЭВМ 60-х годов ХХ века. Моделируемые системы в большинстве случаев содержали порядка 500 частиц, за редким исключением, число частиц доходило до 1000. Чтобы не допустить излишне энергичное смещение атомов кристаллической решётки, было принято решение ограничить максимальную энергию взаимодействия в пределах 400 эВ. Процесс расчёта начинался с задания статической гранецентрированной кристаллической решётки, положения всех атомов которой задавались заранее. Один атом в решётке наделялся произвольной кинетической энергией и направлением движения, после чего стартовал процесс передачи энергии от движущегося атома к соседним. Атомы взаимодействовали с двухчастичными силами отталкивания в форме Борна-Майера:
где B и β – константы взаимодействия, уникальные для каждого материала, r – расстояние между взаимодействующими частицами. Также учитывалась когезионная3 связь атомов в кристалле – к каждом атому на границе кристалла прикладывалась постоянная внутренняя сила. Вычисления проводились до того момента, пока взаимодействия в решётки не прекращались и кристалл «замирал» в повреждённом состоянии. Для разных начальных энергий проводилось несколько «прогонов», чтобы собрать репрезентативную выборку начальных условий. Результаты расчётов подтвердили ранее высказанные предположения, что в низкоэнергетических процессах повреждения кристаллов образуются вакансии и появляются междоузельные атомы. Кроме того, показано, что возникновение цепочек столкновения зависит от направления и носит пороговый характер, хоть и с довольно низкой энергией. Цепочки в направлении (110) образуются при энергиях порядка 30 эВ, в направлении (100) – порядка 40 эВ. При более высоких энергиях цепочки взаимодействия расфокусируются. Волнения в кристалле после повреждений умеренной энергии имеют сходства с тепловыми всплесками, однако перенос энергии далёк от изотропного, как предсказывают модели тепловых всплесков в материалах с кубической кристаллической решёткой. Работа авторов показала возможность численного моделирования событий радиационного повреждения на ЭВМ, пусть и с ограничениями мощности машин того времени. В статье [21] впервые для расчётов межатомного взаимодействия в компьютерном эксперименте применён двухчастичный потенциал взаимодействия Леннарда-Джонса. Целью работы было изучение возможности применения классической динамики двухчастичного взаимодействия в поле центральных сил для корректного описания движения атомов в жидком аргоне и определение пространственно-временных характеристик нейтронного рассеяния. Важность работы было обусловлена прежде всего тем, что к 60-ым года ХХ века теоретиками не была построена общая модель двухчастичного взаимодействия, которая могла бы объяснить наблюдаемые нейтронные спектры. Численный эксперимент проводился при заданной температуре аргона TAr= 94,4 К и плотности ρAr = 1,374 г/см3. Расчётная модель была построена с использованием двухчастичного потенциала взаимодействия Леннарда-Джонса. Частицы с одинаковой массой, атомы аргона, взаимодействовали с потенциалом
где r – расстояние между частицами, σ – масштаб расстояния, ε – масштаб энергии. Для вычислений значение ε выбрано так, что 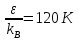 , где kB – постоянная Больцмана. Масштаб длины σ = 3,4 Å. Для увеличения скорости вычислений и сокращения объёма затрачиваемой памяти, под вычисление попадали только те частицы, расстояния между которыми было меньше 2,25σ. , где kB – постоянная Больцмана. Масштаб длины σ = 3,4 Å. Для увеличения скорости вычислений и сокращения объёма затрачиваемой памяти, под вычисление попадали только те частицы, расстояния между которыми было меньше 2,25σ. В начале расчёта 864 одинаковые частицы размещались в случайных позициях внутри кубической ячейки с линейным размером L = 10,229σ, что даёт плотность, равную 1,374 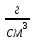 . К расчётной области применялись периодические граничные условия, что позволило расширить исходную ячейку на 26 её «изображений» с координатами, получаемыми добавлением к координате или вычитанием из координаты частицы значения L. При таком подходе плотность частиц остаётся постоянной: частиц, вылетевшая через одну стенку ячейки, тут же появляется на другой её стороне. Шаг по времени принят равным 10-14 секунд. Единственной отслеживаемой в ходе расчёта величиной была среднеквадратичная скорость частиц, выраженная в температурных единицах . К расчётной области применялись периодические граничные условия, что позволило расширить исходную ячейку на 26 её «изображений» с координатами, получаемыми добавлением к координате или вычитанием из координаты частицы значения L. При таком подходе плотность частиц остаётся постоянной: частиц, вылетевшая через одну стенку ячейки, тут же появляется на другой её стороне. Шаг по времени принят равным 10-14 секунд. Единственной отслеживаемой в ходе расчёта величиной была среднеквадратичная скорость частиц, выраженная в температурных единицах
где N = 864. Если в начальный момент времени температура в расчётной области не была близка к значению в 90 К, которое и вызывало интерес к исследованию, значение скорости уменьшалось или увеличивалось на постоянную величину и расчёт в системе возобновлялся. Среднее значение температуры в ходе расчётов принято равным 94,4 К. Приняв w1, w2 и w3 за обозначение ширины распределения Максвелла на высотах e-1/2, e-1, e-2. Когда в системе имеет место распределение Максвелла по скоростям, то мы должны получить
если скорость выражена в единицах ( 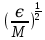 ). Тогда ). Тогда 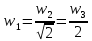 , а численные значения w1, w2 и w3 должны быть 1,78, 2,52 и 3,52 соответственно. В ходе расчёта получены значения 1,77, 2,52, 3,52. , а численные значения w1, w2 и w3 должны быть 1,78, 2,52 и 3,52 соответственно. В ходе расчёта получены значения 1,77, 2,52, 3,52.Для моделирования кулоновских кристаллов метод МД был применён, как указано выше, в работе [7]. Авторами проводилось моделирование системы, содержащей от 2 до 5000 сильно взаимодействующих частиц, находящихся под воздействием гармонической внешней силы. Температура системы поддерживалась много ниже температуры кристаллизации, а параметр Г превышал значение 109. После установления в системе чёткого разделения частиц на 11 оболочек, сравнивались параметры полученных структур из трёх моделей: МД, геометрической и «луковичной» (onion-shell). В качестве величин для сравнения были выбраны: межчастичное расстояние, число заполнения, постоянная Маделунга4. Для получения устойчивой кристаллической решётки из однокомпонентной плазмы к системе была приложена внешняя сила, которая в состоянии равновесия нейтрализует действие силы Кулона во внутренней области
где ri– радиус-вектор расстояния между частицами, K – константа упругости. Кулоновское взаимодействие между частицами описывается выражением
где q – заряд частиц. Во внешней области сохраняется воздействие эффективной связывающей силы. Уравнением движения имеет вид:
Результаты, полученные в результате моделирования сферических кулоновских кристаллов по методу МД, хорошо согласуются с теоретическими значениями ранее указанных параметров, полученными путём соединения геометрической и «луковичной» модели. В геометрической модели элементарные ячейки состоят их двух смещённых параллельных плоскостей равносторонних треугольников; в «луковичной» модели – поверхности однородной заряжены. Теоретические и экспериментальные значения параметра Маделунга находятся в хорошем согласии, но их значение выше, чем предполагается для ОЦК5 решётки, что указывает на преобладание на поверхности кулоновских кристаллов гексагональных структур даже при большом количестве частиц. |

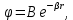
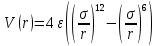 ,
,