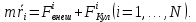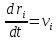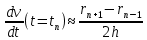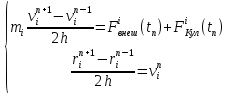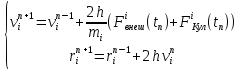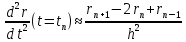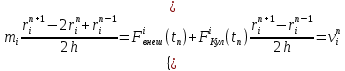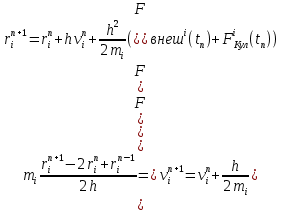Грабовский Д.Е. диплом текст. 1. Кулоновские кристаллы 2 1 История открытия 2

• Название: 1. Кулоновские кристаллы 2 1 История открытия 2
• Дата: 27.05.2022
• Размер: 1.58 Mb.
• Имя файла: Грабовский Д.Е. диплом текст.docx
• Тип: Документы; #553377
• страница: 5 из 6

2.2 Потенциалы взаимодействия

Четыре первых потенциала в таблице 1 – так называемые парные потенциалы. Парный потенциал – функция одного аргумента, расстояния между частицами, которая позволяет полностью описать их взаимодействие, не принимая во внимание остальные частицы системы. Именно приближением парного потенциала пользуются в большинстве задач, решаемых методами молекулярной динамики. Он позволяет обсчитывать системы с миллионами частиц, однако несколько ограничен в области применения. В основном парные потенциалы используются для моделирования ионных и ван-дер-ваальсовых кристаллов, но некоторые модификации всё-таки позволяют работать даже с металлическими структурами.

Парные потенциалы обладают бесконечной областью действия, но для минимизации затрат компьютерного времени и мощности, для всех них вводится радиус обрезания r_c. Радиус обрезания – такое наибольшее расстояние между частицами, для которого рассчитывается потенциал взаимодействия, и частицы вообще считаются взаимодействующими. Такой подход обусловлен следующими факторами:

• 
  число пар взаимодействующих частиц растёт с числом частиц N как N². Использование радиуса обрезания сокращает число соседних частиц, находящихся во взаимодействии, в десятки раз;
  
• 
  при моделировании больших систем зачастую используются периодические граничные условия⁷ (ПГУ). При бесконечной области действия потенциала приходится считать, что каждая частица взаимодействует со своим периодическим образом, что неверно.
  

Метод погружённого атома (EAM – EmbeddedAtomMethod) относится к многочастичным методам. Расчёт силы взаимодействия с использованием многочастичных потенциалов становится заметно труднее – нужно учитывать, что любое изменение полной потенциальной энергии системы, которое происходит из-за смещения i-той частицы, даёт вклад в силу, действующую на эту частицу. Расчёт полной потенциальной энергии в таких моделях происходит по формуле, указанной в таблице 1. Многочастичные модели обычно применяются для моделирования металлов, сплавов и твёрдых материалов в целом.

2.3 Методы интегрирования уравнения движения

Ранее рассмотренное выражение (10) представляет собой дискретную форму записи уравнения движения второго закона Ньютона. Вместе с выбранным потенциалом взаимодействия они образуют центральную часть вычислений по методу МД. Для удобства, продублируем (10) ниже.

(10)

Индекс i соответствует номеру расчётной частицы, 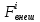– сила, действующая на взаимодействующую частицу извне, соответствует потенциалу ловушки; 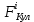– сила кулоновского взаимодействия между частицами; 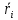– вторая производная от координаты по времени, ускорение частицы. Скорость частицы, в свою очередь, определяется выражением

(11)

Рассмотрим несколько методов интегрирования уравнения (10):

1) Схема с перешагиванием [28]. Производную от координаты заменим на центральную разностную производную:

(12)

где t_n = nh– момент времени n, h – шаг по времени. Подставим (12) в (11) и аналогично преобразуем производную от скорости. Получим систему уравнений

(13)

Тогда, выразив из (13) координату и скорость i частицы в n момент времени, получим следующее:

(14)

2) Схема Верле [29]. Вместо нахождения первой производной от скорости, будем в (10) искать вторую производную по координате. Вторую производную заменим её дискретным аналогом:

(15)

Применяя схему Верле, получим систему уравнений, аналогичную (14)

(16)

3) Скоростная модификация схемы Верле [30]. В скоростной модификации схемы Верле для определения положения частицы в n+1 момент времени необходимо знать положение и скорость частицы в n момент времени. Скорость в момент времени n+1 рассчитывается с учётом того, что силы взаимодействия в n и n+1 момент времени известны. Тогда, применяя ту же разностную производную, что и в пункте 2, получим итерационную схему:

(17)