шпаргалка по основным темам линейной алгебры в сжатом формате, бери и нарезай на маленькие листики, в гармошку складывай и польз. 1. Лин Пространства
 Скачать 485.79 Kb. Скачать 485.79 Kb.
|
|
1.Лин Пространства Некоторые множ-ва наз-ся ЛП если выполнены 3 требования: 1)выполнена операция сложения внутр-яя в ЛП x+y∈ЛП.2)операция умножения внутр-яя в ЛП αx∈ЛП.3)1)комунитативность x,y∈ЛП ,x+y=y+x.2)ассоциативность (x+y)+z=x+(y+z) 3)сущ нулевого элемента x+0=x;4)сущ отрицат элемента x+(-x)=0;5)сущ единицы 1*x=x 6)α(βx)= (αβ)x ∀α,β∈IR, ∀x∈ЛП;7) (α+β)x= αx+βx Дистрибутивность по сложению чисел; 8)α(x+y)= αx+ αy Дист-ть по сложению векторов 2.Линейная зависимость и независимость векторов Наз-ся лин независимой если справедливо:1) 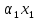 + +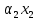 =0,лин коомб эл-ов в этой системе обращ-ся в 0 тогда когда эти числа обр-ся в 0 =0,лин коомб эл-ов в этой системе обращ-ся в 0 тогда когда эти числа обр-ся в 02)если 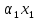 + +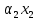 =0 пусть число эл-ов в сист-ме 1 =0 пусть число эл-ов в сист-ме 1 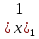 =0 a){0} α∈IR, α≠0-> α*0=0; αx=0→αx=0x+0 б){x}-лин не завис =0 a){0} α∈IR, α≠0-> α*0=0; αx=0→αx=0x+0 б){x}-лин не завис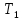 Для того чтобы система эл-ов была линейно зависимой тогда и только тогда,когда хотябы один элемент яв-ся лин-ой коомбинацией Для того чтобы система эл-ов была линейно зависимой тогда и только тогда,когда хотябы один элемент яв-ся лин-ой коомбинацией 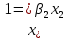 + +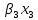 +… +…Размерность прост-ва – макс. число содержащихся в нем линейно независимых векторов. Базис-сис-ма векторов,обл-ая св-ми:1)лин не завис2)всякий др вектор из ЛП яв-ся лин коомб 3.Определение евклидова прост-ва.Аксиомы и пр ЛП наз-ся евклидовым,если появ-ся ф-ия в этом выр-ие 1)(x,y)=(y,x)-семетричность сколяр произведения 2)(x+y,z)=(x,z)+(y,z)-аддативность3)(λx,y)=λ(x,y)-однородность4)(x,y+z)=(x,y)+(x,z);5)(x,λy)=λ(x,y);6)(x,0)=0∈R=(x,0*y)=0(x,y)=0; 7)(x,z)=(y,z) ∀z∈ЛП→x=y→(x,z)-(y,z)=0; 6.Опр матрицу перехода к новому базису и изложите порядок Матрицей лин оператора 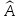 : Xn → Ym в базисах e1, .. , en и f1, … , fm наз-ся матрица размера m × n , у которой : Xn → Ym в базисах e1, .. , en и f1, … , fm наз-ся матрица размера m × n , у которой1) столбцы опр-ся как координатные столбцы образов базисных векторов пространства Xn : 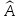 e1, … , e1, … , 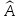 en в базисе пространства Ym ; en в базисе пространства Ym ;2) строки опр-ся как коэффициенты в выражении координат образа произвольного вектора ч/з координаты самого этого вектора. A=( 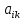 )= )=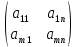 При изменении базиса ЛП матрица оператора изменяется. Пусть в простр-ве X произошел переход от базиса e = {e1, ... , en} к базису e' = {e'1, ... , e'n} . Связь между матрицей Ae оператора A в базисе e и матрицей Ae' этого оператора в базисе e' задается формулой 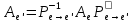 , ,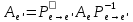 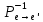 , ,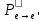 - матрица перехода от базиса e к базису e' и обратная к ней. - матрица перехода от базиса e к базису e' и обратная к ней.7)ЛИНЕЙНЫЙ ОПЕРАТОР И ЕГО МАТРИЦА, ПЕРЕХОД К НОВОМУ БАЗИСУ:Оператор A, действующий в ЛП x,y наз-ся лин-ым оператором, если A(U+V)=A(U)+A(V) и A(αu)=αA(u) для любых U,V∈X и для любого числа α. Если пространства X и Y совпадают, то оператор действует в пространстве X. Переход к другому базису Рассмотрим линейный оператор A, действующий в конечномерном линейном пространстве X, dim(X)=n и пусть 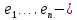 базис в X. Обозначим через A базис в X. Обозначим через A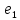 =( =(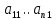 ),..,A ),..,A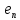 =( =(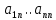 )образы базисных векторов )образы базисных векторов 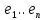 . . Матрица столбцами которой яв-ся координаты образов базисных векторов, наз-ся матрицей линейного оператора в заданном базисе. Доказано, что каждому линейному оператору, действующему в n-мерном линейном пространстве, отвечает единственная квадратная матрица порядка n; и обратно каждая квадратная матрица порядка n задает единственный линейный оператор, действующий в этом пространстве. При этом соотношения с одной стороны, связывают координаты образа Y=AX с координатами прообраза x, с другой стороны, описывают действие оператора, заданного матрицей A. При изменении базиса линейного пространства матрица оператора, очевидно, изменяется. Пусть в пространстве X произошел переход от базиса e={ 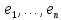 }к базису e’={ }к базису e’={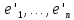 } . Связь между матрицей } . Связь между матрицей 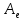 оператора A в базисе e и матрицей оператора A в базисе e и матрицей 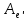 этого оператора в базисе e’ задается ф-лой.Ae’= этого оператора в базисе e’ задается ф-лой.Ae’=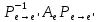 , Ae’= , Ae’=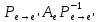 Здесь 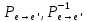 матрица перехода от базиса e к базису e’ и обратная к ней. матрица перехода от базиса e к базису e’ и обратная к ней. 8)СОБСТВЕННЫЕ ЗНАЧЕНИЯ, СОБСТВЕННЫЕ ВЕКТОРЫ ОПЕРАТОРОВ, ПОРЯДОК ИХ НАХОЖДЕНИЯ, СВОЙСТВА СОБСТВЕННЫХ ВЕКТОРОВ, ОТВЕЧАЮЩИХ ОДНОМУ И РАЗНЫМ СОБСТЕННЫМ ЗНАЧЕНИЯМ:Ненулевой вектор x в линейном пространстве L наз-ют собственным вектором линейного оператора A: L → L, если для некоторого действительного числа λ выполняется соотношение Ax = λx. При этом число λ наз-ют собственным значением линейного оператора A.Иными словами, собственный вектор – такой вектор, который под действием лин оператора переходит вколлинеарный вектор, т.е. просто умножается на некоторое число. В отличие от него, несобственные векторыпреобразуются более сложно. Запишем в виде системы и перенесем все слагаемые в левую часть: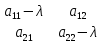 = 0 = 0Это ур-е с неизвестным наз-ют характеристич ур-ем матрицы А (линейного оператора). Корнями которого яв-ся собственные значения. СВ-ВА:Пусть собственные знач-я λ1, ..., λr лин-го оператора A попарно различны. Тогда сис-ма соответствующих им собственных векторов e1, ..., er линейно независима. J Док-во опирается на метод математической индукции, проводимый по количеству r векторов в системе. При r = 1 утверждение теоремы верно, так как линейная независимость системы из одного вектора означает, что этот вектор ненулевой, а собственный вектор, согласно определению 4.3, является ненулевым. Пусть утверждение верно при r = m, т.е. для произвольной системы из m собственных векторов e1, ..., em. Добавим к системе векторов еще один собственный вектор em+1, отвечающий собственному значению λm+1, и докажем, что расширенная таким способом система векторов останется линейно независ. Рассмотрим произвольную линейную комбинацию полученной системы собственных векторов и предположим, что она равна нулевому вектору: α1e1 + ... + αmem + αm+1em+1 = 0. (1) К равенству (1) применим линейный оператор A и в результате получим еще одно векторное равенство α1Ae1 + ... + αmAem + αm+1Aem+1 = 0. Учтем, что векторы e1, ..., em+1 яв-ся собственными: α1λ1e1 + ... + αmλmem + αm+1λm+1em+1 = 0. (2) Умножив равенство (1) на коэффициент λm+1 и вычтя его из равенства (2), получим лин комбинацию векторов e1, ..., em, равную нулевому вектору: α1(λ1 −λm+1)e1 + ... + αm(λm −λm+1)em = 0. Cистема векторов e1, ..., em, линейно независима, вывод, что у полученной лин комбинации все коэф-ы равны нулю: αk (λk −λm+1) = 0, k = 1, m. (4.9) Поскольку все собственные значения λi попарно различны, то из равенств (4.9) следует, что α1 = α2 = ... = αm = 0. Значит соотношение (1) можно записать в виде αm+1em+1 = 0, а т.к. вектор em+1 ненулевой, то αm+1 = 0.Получаем, что равенство (1) выполняется лишь в случае, когда все коэф-ы αi, i = 1, m+1, равны нулю.Доказали, что система векторов e1, ..., em, em+1 линейно независима. 9)МЕТОД ПРИВЕДЕНИЯ МАТРИЦЫ К ДИАГОНАЛЬНОМУ ВИДУ:Нормальную (в частности симметричную) матрицу A можно привести к диагональному виду преобразованием подобия — A = TΛT−1;Λ = diag(λ1,..., λN) — это диагональная матрица, элементами которой яв-ся собственные значения матрицы A, а T —матрица, составленная из соответствующих собственных векторов матрицы A, т.е. T = (v1,...,vN). 12.квадратичной формой n переменных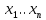 ,принимающих числовые значения , наз-ся числовая ф-ия вида ,принимающих числовые значения , наз-ся числовая ф-ия вида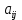 - числа, называемые коэффициентами квадратичной формы.Матрицей квадратич. формы n переменных - числа, называемые коэффициентами квадратичной формы.Матрицей квадратич. формы n переменных 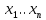 , наз-ся симметрическая матрица порядка n, элементы главной диагонали которой совпадают с коэф-ми при квадратах переменных, а каждый недиагональный элемент, расположенный в i-ой строке j-ом столбце, равен половине коэфициента при , наз-ся симметрическая матрица порядка n, элементы главной диагонали которой совпадают с коэф-ми при квадратах переменных, а каждый недиагональный элемент, расположенный в i-ой строке j-ом столбце, равен половине коэфициента при 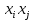 в квадратичной форме.Пр. в квадратичной форме.Пр. 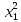 +4 +4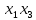 имеет матрицу имеет матрицу 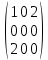 13.Метод Лагранжа.Один из методов преобразования квадратичной формы к каноническому виду путем замены переменных состоит в последовательном выделении полных квадратов.Пр.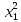 -4 -4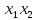 Для преобразования ее к канонич виду выделим полный квадрат по Для преобразования ее к канонич виду выделим полный квадрат по 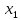 для этого соберем все слагаемые,содержащие для этого соберем все слагаемые,содержащие 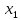 и дополним до полного квадрата . и дополним до полного квадрата .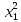 -4 -4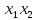 = =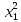 -4 -4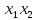 +4 +4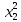 -4 -4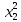 = =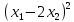 -4 -4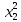 .Введя новые переменные переменные .Введя новые переменные переменные 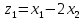 ; ;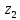 = =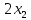 ,получим квадратич форму канонич вида ,получим квадратич форму канонич вида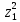 - -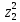 14)2Й МЕТОД ПРИВЕДЕНИЯ КВАДРАТИЧ. ФОРМЫ К КАНОНИЧЕСКОМУ ВИДУВид:A(x,x)=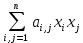 в евклидовом пространстве в евклидовом пространстве 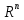 .Тк ее матрица A=( .Тк ее матрица A=(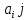 )симметрична,то она может быть представлена в виде A=UD )симметрична,то она может быть представлена в виде A=UD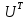 ,D-диагональная матрица,на диагонали которой стоят собств числа матрицы,а U-ортогональная матрица.Столбцы матрицы U яв-ся координатами некоторого ортонормированного базиса ,D-диагональная матрица,на диагонали которой стоят собств числа матрицы,а U-ортогональная матрица.Столбцы матрицы U яв-ся координатами некоторого ортонормированного базиса 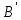 =( =(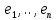 ),в котором матрица А имеет диагональный вид D ,значит квадратич форма-искомый канонич вид.Соотв преобразования координат опр-ся соотношением ),в котором матрица А имеет диагональный вид D ,значит квадратич форма-искомый канонич вид.Соотв преобразования координат опр-ся соотношением  =U =U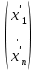 16)Построение преобразующей матрицы приводящей симметрич матрицу к диагон виду.Для любой симметрической матрицы M сущ-ет такая ортогональная матрица U, что UтMU = Λ, где Λ = diag(λ1, ..., λn) — диагональная матрица, диагональными элементами которой яв-ся собственные значения матрицы M, повторяющиеся согласно их кратности. 16)Построение преобразующей матрицы приводящей симметрич матрицу к диагон виду.Для любой симметрической матрицы M сущ-ет такая ортогональная матрица U, что UтMU = Λ, где Λ = diag(λ1, ..., λn) — диагональная матрица, диагональными элементами которой яв-ся собственные значения матрицы M, повторяющиеся согласно их кратности. Преобразование с ортогональной матрицей U иногда наз-ют ортогональным преобразованием матрицы A. Теорема: любая симметрическая матрица ортогональным преобразованием приводится к диагональному виду. Чтобы найти соотв. матрицу U необходимо: 1) найти собственные значения матрицы M; 2) для каждого собственного значения найти набор собственных векторов, соотв-их этому собственному значению, при этом эти собственные векторы должны быть линейно независимыми и их кол-во должно равняться кратности собственного значения; 3) преобразовать системы собственных векторов, полученные для каждого собственного значения, в ортонормированные при помощи процесса ортогонализации Грама — Шмидта Объединить ортонормированные системы для каждого собственного значения в единую систему векторов, которая будет ортонормированным базисом евклидова пространства; 4) выписать матрицу U, столбцами которой яв-ся координаты векторов построенной ортонормированной системы. 17)Подобные матрицы Две прямоугольные матрицы A и B одной размерности I×J эквивалентны, если существуют такие квадратные матрицы S, размерности I×I, и T, размерности J×J, чтоB = SAT. Эквивалентные матрицы имею один и тот же ранг. Две прямоугольные матрицы A и B одной размерности N×N подобны, если существует такая невырожденная матрица T,чтоB = T−1AT. Матрица T наз-ся преобразованием подобия. Подобные матрицы имеют один и тот же ранг, след, определитель и спектр. Св-ва подобных матриц 1. Каждая квадратная матрица подобна самой себе: A=E−1AE 2. Если матрица B подобна матрице A, то и A подобна B:B=S−1⋅A⋅S ⇔ A=T−1⋅B⋅TB=S−1⋅A⋅S ⇔ A=T−1⋅B⋅Tпри T=S−1T=S−1. 3. Если матрица A подобна матрице B, а B подобна C, то A подобна C: 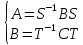 →A= →A=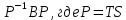 4. Подобие яв-ся частным случаем эквивалентных преобразований. 5. В случае ортогональности преобразующей матрицы подобные матрицы яв-ся конгруэнтными. Св-ва 4, 5. Эквивалентные матрицы связаны соотношением B=SATB=SAT, где SS и TT — невырожденные матрицы. Если T=S−1T=S−1, то получаем преобразование подобия B=SAS−1⇔A=S−1BSB=SAS−1⇔A=S−1BS. Если же матрица SS ортогональная (S−1=ST)(S−1=ST), то подобные матрицы, связанные равенством B=S−1ASB=S−1AS, оказываются конгруэнтными,т к B=STASB=STAS *-1-это стпень ||  x||= x||= = = = = =|λ| ||x|| =|λ| ||x||19)Ф-ия многих переменных Отображение, которое упорядоченному набору из n чисел ставит в соответствие число, т.е. отображение вида f: A → R, где A ⊂ Rn, n > 1, наз-ют ф-ей нескольких переменных. Данное определение согласуется с определением ф-ии действительного переменного, которое соответствует общему определению ф-ии нескольких переменных в случае n = 1. Таким образом, понятие ф-ии нескольких переменных можно рассматривать как обобщение понятия ф-ии действительного переменного Множ-во D(f) = A точек из Rn, в которых определена ф-ия f: A ⊂ Rn → R, наз-ют областью определения ф-ии f, а множество R(f) = = {y ∈R: y = f(x), x ∈ D(f)} — областью значений ф-ии. Точку a ∈ Rn наз-ют предельной точкой множества A ⊂ Rn, если в любой ее проколотой окрестности есть точки из множ-ва A. Предельная точка множ-ва может либо принадлежать этому множ-ву, либо не принадлежать ему. Отметим, что если точка a яв-ся предельной для множ-ва A, то в любой окрестности U(a,ε) этой точки содержится бесконечно много точек множ-ва A. Точку a наз-ют изолированной точкой множ-ва A, если a ∈ A и сущ-ет такая ее проколотая окрестность, которая не содержит точек из множ-ва A. Отметим, что любая точка a ∈ A яв-ся либо предельной точкой A, либо изолированной точкой A. Пусть заданы ф-ия нескольких переменных f: Rn → R, множ-воA ⊂ D(f), включенное в область определения D(f) ф-ии f, и предельная точка a множ-ваA . Точку b ∈R наз-ют пределом ф-ии f в точке a по множ-ву A, если для любой ε-окрестности U(b,ε) точки b сущ-ет такая проколотая δ-окрестность ◦U(a,δ) точки a, что f(x) ∈ U(b,ε) при x ∈ ◦U(a,δ)∩A, т.е. ∀U(b,ε) ⊂Rm ∃ ◦U(a,δ) ⊂Rn ∀x ∈ ◦U(a,δ)∩A : f(x) ∈ U(b,ε). В этом случае записывают b=  ,или f(x)→b при x→a по множ-ву A ,или f(x)→b при x→a по множ-ву AФ-ию нескольких переменных f: A ⊂ Rn → R наз-ют непрерывной в точке a ∈ A, предельной для множ-ва A, если сущ-ет предел ф-ии f при x→ A a, равный значению ф-ии в этой точке, т.е. если lim (x→ a)f(x) = f(a). Как оговорено в опр., точка a не только принадлежит множ-ву A, но и яв-ся его предельной точкой, поскольку рассматривается предел ф-ии в точке a по множ-ву A. Ф-ию f: A ⊂ Rn → Rm считают непрерывной в каждой точке a ∈ A, которая яв-ся изолированной точкой множ-ва A. 20)Частные производные Пусть ф-ия нескольких переменных f: Rn → R определена в некоторой окрестности точки a = (a1, ..., an) ∈Rn. Тогда в некоторой окрестности точки a1 ∈R определена ф-ия одного переменного ϕ1(x1) = f(x1,a2,...,an), которая получается из ф-ии f(x) при фиксированных значениях всех аргументов, кроме первого. Производную ϕ/ (a1) ф-ии ϕ(x1) в точке a1 ∈ R наз-ют частной производной ф-ии нескольких переменных f в точке a по переменному x1. Аналогично можно определить частные производные ф-ии f и по другим переменным. Частную производную ф-ии f в точке a по переменному xi обозначают след. образом:  или или  (a) (a)Предположим, что ф-ия нескольких переменных f: Rn → R во всех точках в некоторой окрестности U(a,δ) точки a имеет частную производную f0 xi(x). Эта частная производная сама яв-ся ф-ей нескольких переменных, определенной в окрестности U(a,δ), и может оказаться, что она имеет частную производную в точке a, например по переменному xj. Частную производную  или или  (a) (a)Ф-ии f0 xi(x) наз-ют частной производной второго порядка ф-ии f(x) в точке a по переменным xi и xj и обозначают  , ,  (a) или (a) или (a) (a)Частные производные высшего порядка вводятся так же, как и частные производные 2го порядка. Частную производную k-го порядка ф-ии нескольких переменных опр-ют как частную производную 1го порядка от некоторой частной производной (k−1)-го порядка этой ф-ии. 21. Равенство смешанных производных независимо от порядка дифференцирования. Смешанные частные производные одной и той же ф-ии, отличающиеся лишь порядком дифференцирования, равны между собой при условии их непрерывности. Такое св-во наз-ся равенством смешанных производных. Определение смешанной производной Пусть дана достаточно гладкая ф-ия 𝑓{\displaystyle f} многих переменных:f=f(  … … ) )Мы можем взять частную производную этой ф-ии по одному из аргументов {\displaystyle x_{i}}  , считая остальные аргументы постоянными параметрами. В результате мы получим новую ф-ию: , считая остальные аргументы постоянными параметрами. В результате мы получим новую ф-ию:Эта новая ф-ия тоже зависит от остальных аргументов как от параметров. То есть численное значение  {\displaystyle \phi } в общем случае зависит от тех же переменных {\displaystyle x_{1},x_{2},\dots x_{n}} {\displaystyle \phi } в общем случае зависит от тех же переменных {\displaystyle x_{1},x_{2},\dots x_{n}} , что и оригинальная ф-ия 𝑓{\displaystyle f}: , что и оригинальная ф-ия 𝑓{\displaystyle f}:Если ф-ия 𝜑{\displaystyle \phi } окажется достаточно гладкой, то мы можем и её продифференцировать, взяв частную производную по тому же самому или по другому аргументу {\displaystyle x_{j}}  : :Если  {\displaystyle j\neq i}, то выражение в правой части равенства (4) наз-ся смешанной производной. {\displaystyle j\neq i}, то выражение в правой части равенства (4) наз-ся смешанной производной.Основа теоремы Для достаточно гладкой ф-ии многих переменных значение смешанной производной не зависит от порядка дифференцирования:  Доказательство теоремы Как указано выше, для док-ва теоремы можно не рассматривать зависимость ф-ии от третьих аргументов. Поэтому для простоты записи изменим обозначения {\displaystyle x_{i},x_{j}}  на x,y то есть будем рассматривать такую ф-ию 2х переменных:f=f(x,y) на x,y то есть будем рассматривать такую ф-ию 2х переменных:f=f(x,y)Также для упрощения формул будем обозначать частные производные индексами внизу ф-ии: Пусть в точке {\displaystyle (x,y)}(x,y) сущ-ет смешанная производная: Предположим, что смешанная производная  сущ-ет в точке {\displaystyle (x,y)}(x,y), а также сущ-ет 1я производная сущ-ет в точке {\displaystyle (x,y)}(x,y), а также сущ-ет 1я производная  вдоль прямой y=const вдоль прямой y=constДалее, разность производных равна производной от разности, поэтому превращаем формулу (9) в: Это преобразование никаких доп. условий не накладывает, поскольку разность дифференцируемых ф-ий всегда является функцией дифференцируемой. Далее, разность в квадратных скобках формулы (10) можно записать в виде определённого интеграла от производной: Нужно, чтобы сущ-ала частная производная  вдоль прямой {\displaystyle y=const}y=const. вдоль прямой {\displaystyle y=const}y=const.Теперь частную производную по игрек в формуле (11) запишем согласно определению производной как предела: Как видно, надо, чтобы частная производная {\displaystyle f_{x}}  существовала не только на прямой {\displaystyle y=const}y=const, но в некоторой 2хмерной окрестности точки {\displaystyle (x,y)}(x,y). существовала не только на прямой {\displaystyle y=const}y=const, но в некоторой 2хмерной окрестности точки {\displaystyle (x,y)}(x,y).Далее, разность интегралов равна интегралу от разности, причём под знак интеграла можно внести постоянный множитель  : :Это преобразование также не накладывает доп. условий, поскольку разность интегрируемых ф-ий яв-ся ф-ей интегрируемой. По теореме Лагранжа, подынтегральное выражение в формуле (13) равно производной в средней точке: Средняя точка яв-ся ф-ей: значения которой лежат в интервале (если, например, {\displaystyle \Delta y>0}∆y>0) Для справедливости (14) нужно существование смешанной производной Для окончания док-ва надо принять, что смешанная производная непрерывна в точке {\displaystyle (x,y)}(x,y) как ф-ия 2х переменных. Значение этой производной в близкой точке(٤,n) {\displaystyle (\xi ,\eta )} равно с точностью до бесконечно малого слагаемого значению производной в точке {\displaystyle (x,y)}(x,y) : {\displaystyle (x,y)} Смешанная производная {\displaystyle f_{yx}}  сущ-ет в 2хмерной окрестности точки {\displaystyle (x,y)}(x,y) и непрерывна в этой точке как ф-ия 2х переменных. сущ-ет в 2хмерной окрестности точки {\displaystyle (x,y)}(x,y) и непрерывна в этой точке как ф-ия 2х переменных.Подставим (14) и (15) в (13): Заметим, что формула (16) эквивалентна формуле (13), а потому интеграл и обе границы сущ-ют. Поскольку подынтегральная ф-ия в (16) интегрируема, а 1е слагаемое  (x,y){\displaystyle f_{yx}(x,y)}яв-ся константой по переменной интегрирования ٤{\displaystyle \xi }, то 2е слагаемое тоже оказ-ся интегрируемым, и мы можем разбить интеграл на сумму 2х интегралов, 1й из которых легко берётся как интеграл от константы: (x,y){\displaystyle f_{yx}(x,y)}яв-ся константой по переменной интегрирования ٤{\displaystyle \xi }, то 2е слагаемое тоже оказ-ся интегрируемым, и мы можем разбить интеграл на сумму 2х интегралов, 1й из которых легко берётся как интеграл от константы:После подстановки (17) в (16) мы можем вынести постоянное слагаемое сначала за пределы первой границы, а затем за пределы другой границы: Покажем, что 2е слагаемое в последнем выражении формулы (18) равно 0. Возьмём произвольное {\displaystyle \epsilon }ε>0. Непрерывность смешанной производной {\displaystyle f_{yx}}  в точке {\displaystyle (x,y)}(x,y) означает, что сущ-ет такое δ>0{\displaystyle \delta },что для каждой точки {\displaystyle (\xi ,\eta )}(٤,n) внутри квадратаI٤-xI<δ,In-yI<δ {\displaystyle |\xi -x|<\delta ,\;|\eta -y|<\delta } справедливо неравенство: в точке {\displaystyle (x,y)}(x,y) означает, что сущ-ет такое δ>0{\displaystyle \delta },что для каждой точки {\displaystyle (\xi ,\eta )}(٤,n) внутри квадратаI٤-xI<δ,In-yI<δ {\displaystyle |\xi -x|<\delta ,\;|\eta -y|<\delta } справедливо неравенство:Если мы возьмём числа>0,Δx<δ,Δy<δ {\displaystyle \Delta x<\delta ,\;\Delta y<\delta }, то интеграл в последнем слагаемом формулы (18) оценивается сверху: Обозначим это слагаемое {\displaystyle L}L: Аналогично (если взять (-ɛ<Δx<0) {\displaystyle -\epsilon <\Delta x<0}), имеем оценку снизу: L>=-ɛ Поскольку положительное число {\displaystyle \epsilon }ε может быть сколь угодно малым, то с необходимостью следует {\displaystyle L=0}L=0. 22. Полный дифференциал ф-ии двух переменных, полный дифференциал 2го порядка. Дифференциалы высоких порядков. Инвариантность полного дифференциала. Полным дифференциалом dz дифференцируемой в точке М(x,y) ф-ии z=f(x,y) наз-ют линейную относительно приращений Δx и Δy часть полного приращения этой ф-ии в точке М: dz=AΔx+BΔy,задается формулой dz=  dx+ dx+ dy dyПолным дифференциалом 2го порядка ф-ии z = f(x, y) наз-ся полный дифференциал от полного дифференциала dz(x, y) 1го порядка при условии, что dx и dy cчитаются постоянными (dx и dy не зависят от x и у).  z=d( z=d( dx+ dx+ dy)= dy)= ( ( dx+ dx+ dy)dx+ dy)dx+ ( ( dx+ dx+ dy)dy= dy)dy= d d +2 +2 dxdy+ dxdy+ d d Аналогично дифференциал n-го порядка - полный дифференциал от дифференциала (n – 1)-го порядка, т. е. dn z(x, y) = d(d(n-1) z(x, y)).   23. Неявная ф-ия многих переменных. Производная от ф-ии, заданной неявно, вторая производная от этой ф-ии.     24)Производная по направлению.Градиент Производной ф-ии по направлению f:  →R в точке a →R в точке a вектора n наз-ют число вектора n наз-ют число  = = -f(a),если этот предел сущ. -f(a),если этот предел сущ.Производная по направлению представляет собой скорость изменения значений ф-ии в точке a в направлении вектора n Связь с градиентом Производную по направлению дифференцируемой по совокупности переменных ф-ии можно рассматривать как проекцию градиента ф-ии на это направление, или иначе, как скалярное произведение градиента на орт направления:  {\displaystyle {\frac {\partial f}{\partial e}}=\nabla f\cdot {\vec {e}}} {\displaystyle {\frac {\partial f}{\partial e}}=\nabla f\cdot {\vec {e}}}Макс. значение в точке производная по направлению принимает, если направление совпадает с направлением градиента ф-ии в данной точке. Градиент.Пусть ф-ию нескольких переменных f:  →R в точке x имеет все частные производные первого порядка.Вектор grad f(x)=( →R в точке x имеет все частные производные первого порядка.Вектор grad f(x)=( ) составленный из частных производных 1го порядка ф-ии f(x) в точке x наз-ют градиентом f в точке x. ) составленный из частных производных 1го порядка ф-ии f(x) в точке x наз-ют градиентом f в точке x.25. Сформулируйте понятие экстремумы ф-ии. Необходимые и достаточные условия экстремума ф-ии в точке Экстремум Экстремум - макс или мин значение ф-ии на заданном множ-ве. Точка, в которой достигается экстремум, наз-ся точкой экстремума. Соответственно, если достигается мин — точка экстремума наз-ся точкой мин, а если макс — точкой макс. Необходимые условия существования экстремумов Теорема Лемма Ферма́ утверждает, что производная дифференцируемой ф-ии в точке экстремума равна нулю. Пусть {\displaystyle x_{0}}  яв-ся точкой экстремума ф-ии {\displaystyle f}f, опр-ой в некоторой окрестности точки {\displaystyle x_{0}} яв-ся точкой экстремума ф-ии {\displaystyle f}f, опр-ой в некоторой окрестности точки {\displaystyle x_{0}} . .Тогда либо производная  не существует, либо {\displaystyle f'(x_{0})=0} не существует, либо {\displaystyle f'(x_{0})=0} . .Эти условия не яв-ся достаточными, так, ф-ия может иметь нуль производной в точке, но эта точка может не быть точкой экстремума, а яв-ся точкой перегиба, как точка (0,0) у ф-ии {\displaystyle f(x)=x^{3}}  . .1е достаточное условие существования экстремума Если в точке x˳ ф-ия непрерывна и в ней производная меняет знак с “+” на “–“, то x˳ - точка макс; Если в точке x˳ ф-ия непрерывна и в ней производная меняет знак с “-” на “+”, то x˳ - точка мин. 2е достаточное условие существования экстремума Пусть f’(x˳)=0 ,если f’’(x˳)>0,x˳- точка мин;если f’’(x˳)<0,x˳- точка макc. Этот признак экстремума ф-ии требует существования производной как минимум до второго порядка в точке x˳. 3е достаточное условие существования экстремума Пусть ф-ия y=f(x) имеет производные до n-ого порядка в ٤-окрестности точки x˳и производные до n+1-ого порядка в самой точке x˳. Пусть f’(x˳)=f’’(x˳)=…  (x˳)=0 и (x˳)=0 и (x˳)≠0 . (x˳)≠0 .Тогда:если n – четное, то x˳ - точка перегиба;если n – нечетное, то x˳ - точка экстремума, причем: Если  (x˳)>0 , то x˳ - точка мин;если (x˳)>0 , то x˳ - точка мин;если  (x˳)<0 , то x˳ - точка макс. (x˳)<0 , то x˳ - точка макс.26. Условный экстремум ф-ии в точке (метод Лагранжа) Метод нахождения условного экстремума ф-ии {\displaystyle f(x)}f(x), где {\displaystyle x\in \mathbb {R} ^{n}}  относительно {\displaystyle m}m ограничений {\displaystyle \varphi _{i}(x)=0} относительно {\displaystyle m}m ограничений {\displaystyle \varphi _{i}(x)=0} , где {\displaystyle i}i меняется от единицы до {\displaystyle m}m. , где {\displaystyle i}i меняется от единицы до {\displaystyle m}m.Составим ф-ию Лагранжа в виде линейной комбинации ф-ии {\displaystyle f}f и ф-ий {\displaystyle \varphi _{i}}  , взятых с коэффициентами, называемыми множителями Лагранжа - {\displaystyle \lambda _{i}} , взятых с коэффициентами, называемыми множителями Лагранжа - {\displaystyle \lambda _{i}} : : {\displaystyle L(x,\;\lambda )=f(x)+\sum _{i=1}^{m}\lambda _{i}\varphi _{i}(x),} {\displaystyle L(x,\;\lambda )=f(x)+\sum _{i=1}^{m}\lambda _{i}\varphi _{i}(x),}где {\displaystyle \lambda =(\lambda _{1},\;\ldots ,\;\lambda _{m})}  Составим систему из {\displaystyle n+m}n+m уравнений, приравняв к нулю частные производные ф-ии Лагранжа {\displaystyle L(x,\;\lambda )}  {\displaystyle x_{j}} {\displaystyle x_{j}}Если полученная система имеет решение относительно параметров {\displaystyle x'_{j}}  {\displaystyle \lambda '_{i}}, тогда точка {\displaystyle x'} {\displaystyle \lambda '_{i}}, тогда точка {\displaystyle x'} может быть условным экстремумом, то есть решением исходной задачи. может быть условным экстремумом, то есть решением исходной задачи. |
