Математика. 1. Логическая структура предложений и их логические формулы
 Скачать 70.58 Kb. Скачать 70.58 Kb.
|
|
1. Логическая структура предложений и их логические формулы 1) Дидактика – это наука о теориях и технологиях образования и обучения. Повествовательное предложение. ( C ® Q ) 2) Студент выполняет работу самостоятельно или обращается за консультацией. Дизъюнкция A v B. 3) Если бы не было статистики, мы даже не подозревали бы о том, как хорошо мы работаем. Импликация A → B 4) Произведение двух чисел рано нулю в том и только том случае, когда хотя бы одно из них равно нулю. Эквиваленция. (А) = fA· А 5) Неправда, что мы не любим поэзию. Отрицание. A→¬¬ A. 2. Являются ли равносильными высказывания «Ревнует – значит любит», «Не ревнует – значит не любит». Импликативная форма высказываний: Если человек ревнует, значит, он любит (A → B). Если человек не ревнует, значит он не любит (неA → неB) Сделаем вывод о истинности и ложности: Таблица истинности:
Указание: сформулируйте высказывания в импликативной форме, запишите их формулы и сделайте вывод с помощью таблиц истинности или соответствующих законов логики. 3. Пары высказываний, являющихся отрицаниями друг друга 1 и 3 4. Отрицание высказываний 1) Некоторые студент не выполнили тест и не сдали вовремя творческое задание. 2) Не каждый солдат, который не мечтает стать генералом, плохой. 5. Примеры универсальных множеств и подмножеств Рассмотрим множество психологов. В него входят подмножества: - детские психологи; - юридические психологи; - клинические психологи. В свою очередь подмножество детских и клинических психологов можно разбить на подмножества: психологов, работающих в муниципальных учреждениях, и психологов, занимающихся частной практикой. Проиллюстрируем это:         Другой пример универсального множества – студенты САФУ. Подмножествами данного множества будут студенты разных факультетов. Внутри каждого подмножества (факультета) можно выделить еще подмножества: очная, заочная или вечерняя формы обучения. Проиллюстрируем это:                          6. Пересечение, объединение, разность и дополнение множеств 1) Объединение: Пришли гости: девочки Юля и Маша, и мальчики Петя, Коля и Феликс. Получилась компания: Юля, Маша, Петя, Коля, Феликс       2) Пересечение: В фирме работают сотрудники, имеющие высшее образование, а также те, кто работает и учится заочно.   3) Разность: Премию получат только те сотрудники фирмы, которые за последние полгода соглашались работать сверхурочно.   Получат премию 4) Дополнение: Выпускники САФУ, получившие диплом психолога, могут поступить на психологические направления послевузовского образования, но уже не в САФУ. А в другие ВУЗы. В этом случае множество будет выпускники САФУ, а дополнение к множеству – те выпускники, которые пошли на психологические специальности в другие ВУЗы.   7  . Задача про студентов и тренинги . Задача про студентов и тренинги ЛР ТМ 130  200 50 140 90 ЭУ 190 На 1 курсе заочной формы обучения ВШ ППФК учатся 340 студентов. Каждый из них должен во время сессии пройти хотя бы один вид тренинга: Таймменеджмент, Эмоциональная устойчивость или Личностный рост. Все три тренинга прошли 50 человек, Эмоциональная устойчивость – 190, Тайм-менеджмент – 200, Личностный рост и Тайм-менеджмент – 130, Личностный рост и Эмоциональная устойчивость – 140, Тайм-менеджмент и Эмоциональная устойчивость – 90. Сколько студентов прошли только тренинг Личностный рост? Решение: На представленных диаграммах видно, что студентов, которые прошли только один тренинг – «Личностный рост» - на первом курсе нет. 8. Задача про восьмиклассников В ходе опроса восьмиклассников некоторой школы было выяснено, сколько времени в неделю (с точностью до 0,5 ч) они затрачивают на занятиях в кружках и спортивных секциях. Получили следующие данные:
1. Представьте собранные данные в наглядной форме, для этого: а) постройте интервальный статистический ряд.
h = 0,90309, округляем до 0,9. Формирование интервала. Найдем начальную точку. Для этого поделим h пополам: 0,9 : 2 = 0,45. Каждая следующая точка интервала находится прибавлением h к предыдущей точке. Получаем интервал:
б) постройте гистограмму и кумуляту относительных частот полученного статистического ряда.
Вычислим частоту и относительную частоту
2. Первичная обработка данных и интерпретация - Мода – это значение ряда, у которого наибольшая частота. Ее рассчитыают по формуле: 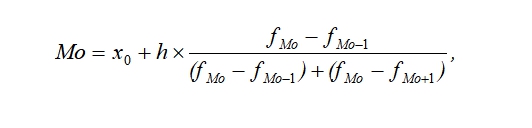 В нашем случае наибольшая частота – это 2. Значит, мода будет равна 2. - Медиана – это среднее значение ряда. Она рассчитывается по формуле: 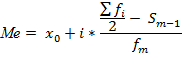 В нашем ряду 50 значений:
Медиана будет равна 3. - Среднее арифметическое – среднее значение математических данных, которое рассчитывается методом сложения всех показателей и деления полученной суммы на количество единиц ряда. Рассчитаем среднее арифметическое для наших данных: (0+0+0+0+1+1+1+1+1,5+1,5+1,5+2+2+2+2+2+2+2+2+2,5+2,5+2,5+2,5+2,5+3+3+3+3+3,5+3,5+3,5+3,5+3,5+3,5+4+4+4+4+4+4+4+4,5+4,5+5+5+5+5+5,5+5,5+6+6) : 50 =2,93 Среднее арифметическое равно 2,93 - Размах – это разница между наибольшим и наименьшим показателем. Размаъ рассчитываем по формуле: R=Xmax-Xmin В нашем случае наибольший показатель равен 6, а наименьший 0. Посчитаем размах: 6 – 0 = 6 - Стандартное отклонение показывает волатильность данных (то, с каким размахом они меняются). Стандартное отклонение рассчитывается по формуле:  Стандартное отклонение = 1,60995 - Коэффициент вариации – это относительное стандартное отклонение, это стандартная мера дисперсии распределения вероятностей или частотного распределения. Он рассчитывается по формуле: Коэффициент вариации = 2,59194. Выводы для педсовета или родительского собрания: В результате математической обработки эмпирических данных удалось установить, что большая часть восьмиклассников образовательного учреждения посещает кружки и секции. Исследование показало, что график работы кружков и секций, выбираемых детьми, чаще всего предполагает 2 занятия в неделю продолжительностью 1 час (мода). В среднем каждый восьмиклассник тратит на кружки и секции в неделю 2,93 часа (среднее арифметическое). Однако разброс данных достаточно большой: есть такие восьмиклассники, которые не посещают занятия в сфере дополнительного образования, а есть те, кто ходит сразу на несколько кружков (размах). Сферы дополнительного образования, которые выбирают восьмиклассники, достаточно разнообразны. Продолжительность занятий и их периодичность также различны. (Стандартное отклонение и коэффициент вариации). Таким образом, в свободное от учебы и приготовления домашнего задания время восьмиклассники развивают свои таланты в сфере дополнительного образования. Исследование показало, что время, которое подростки проводят на кружках и секциях, соответствует требованиям СанПин и возрасту учащихся 8 классов. |
