Логика. логика. 1 Логика это наука о формах и средствах познания мира на ступени абстрактного мышления
 Скачать 330.17 Kb. Скачать 330.17 Kb.
|
|
§ 2. Непосредственные умозаключения Суждение, содержащее новое знание, может быть получено посредством преобразования некоторого суждения. Так как исходное (преобразуемое) суждение рассматривается как посылка, а суждение, полученное в результате преобразования, — как заключение, умозаключения, построенные посредством преобразования суждений, называются непосредственными. К ним относятся: 1) превращение, 2) обращение, 3) противопоставление предикату, 4) умозаключения по логическому квадрату. Выводы в каждом из этих умозаключений получаются в соответствии с логическими правилами, которые обусловлены видом суждения — его количественными и качественными характеристиками. 20) Категорический силлогизм (или просто: силлогизм) – это дедуктивное умозаключение, в котором из двух категорических высказываний выводится новое категорическое высказывание. Логическая теория такого рода умозаключений называется силлогистикой. Она была создана еще Аристотелем и долгое время служила образцом логической теории вообще. В силлогистике выражения "Все S есть P" , "Некоторые S есть P" , "Все S не есть P" , "Некоторые S не есть P" рассматриваются как логические постоянные, т.е. берутся как единое целое. Это не высказывания, а определенные логические формы, из которых получаются высказывания путем подстановки вместо переменных каких-то имен. Подставляемые имена называются терминами силлогизма. Существенным является следующее традиционное ограничение: термины силлогизма не должны быть пустыми или отрицательными. Примером силлогизма может быть: Все жидкости упруги. Вода – жидкость. Вода упруга. В каждом силлогизме должно быть три термина: меньший, больший и средний. Меньшим термином называется субъект заключения (в примере таким термином является термин "вода"). Бо¢льшим термином именуется предикат заключения ("упруга"). Термин, присутствующий в посылках, но отсутствующий в заключении, называется средним термином ("жидкость"). Меньший термин обозначается обычно буквой S, больший – буквой P и средний - M. Посылка, в которую входит больший термин, называется большей. Посылка с меньшим термином называется меньшей. Большая посылка записывается первой, меньшая – второй. Логическая форма приведенного силлогизма такова: Все М есть P Все S есть М Все S есть P Структура силлогизма подчинена определенным логическим правилам, без соблюдения которых невозможно построить силлогизм. Эти правила можно разбить на две группы: правила терминов и правила посылок. а) Правила терминов. 1. В каждом силлогизме должно быть только три термина – большой, меньший и средний. Это правила требует не только соответствующего построения силлогизма, но и однозначности среднего термина в обеих посылках. 2. Средний термин должен быть распределен, то есть взят в полном объеме, хотя бы в одной из посылок. Для этого он должен быть или субъектом общего суждения, или предикатом отрицательного суждения. Если же средний термин взят не в полном объеме в обеих посылках, то выполнить свою роль связующего звена он не сможет, и точный вывод получить невозможно. Например, в посылках «Некоторые студенты – мастера спорта» и «Все старосты учебных групп - студенты» средний термин «студенты» не распределен, поэтому сделать вывод, есть ли мастера спорта среди старост групп не представляется возможным. 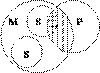 3. Термин, не распределенный в посылках, не может быть распределен в заключении. Из общих суждений-посылок: «Все птицы летают с помощью крыльев» и «Все птицы – теплокровные животные» нельзя получить в качестве вывода общее суждение. Меньший термин «теплокровные животные» стоит на месте предиката в утвердительной посылке и поэтому не распределен. Следовательно, в выводе его нужно брать не в полном объеме.  4. Из двух частных посылок невозможно сделать вывод. В этом случае нельзя установить объемные отношения между терминами силлогизма, поэтому определенный вывод не получается. Например, из посылок: «Некоторые члены Академии наук - химики» и «Некоторые биологи – члены Академии наук» никакой определенный вывод не следует. 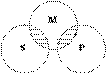 5. Если одна посылка частная, то вывод будет частным. Из посылок: «Все участники кросса - спортсмены» и «Некоторые студенты-отличники – участники кросса» общий вывод невозможен. Нельзя утверждать, что все студенты-отличники – спортсмены, так как речь идет только о части объема меньшего термина. 6. Из двух отрицательных посылок нельзя сделать вывод. 7. Если одна посылка отрицательная, то вывод будет отрицательным. Например: «Всякое пребывание на свежем воздухе полезно. Пребывание на свежем воздухе при низкой температуре опасно. Следовательно, пребывание на свежем воздухе при низкой температуре может принести вред здоровью».  Таковы общие правила, которые следует учитывать при составлении силлогизма. 21) Простой категорический силлогизм Простой категорический силлогизм – это одно из наиболее простых и часто встречающихся умозаключений. Он состоит из двух посылок. В первой посылке говорится об отношении терминов А и В, во второй – об отношениях терминов В и С. На основании этого делается вывод об отношении терминов А и С. Такой вывод возможен потому, что обе посылки содержат общий термин В, который опосредует отношение между терминами А и С. Приведём пример: Все рыбы не могут жить без воды. Все акулы – это рыбы. Следовательно, все акулы не могут жить без воды. В данном случае, термин «рыбы» – это общий термин для двух посылок, и он помогает связать термины «акулы» и «существа, способные жить без воды». Общий термин для двух посылок принято называть средним термином. Субъект заключения (в нашем примере это «акулы») называют меньшим термином. Предикат заключения («существа, способные жить без воды») называют бóльшим термином. Соответственно, посылку, содержащую меньший термин, называют меньшей посылкой («Все акулы – это рыбы»), а посылку, содержащую больший термин, – бóльшей посылкой («Все рыбы не могут жить без воды»). Естественно, в рассуждении посылки могут находиться в любой последовательности. Однако для удобства проверки правильности силлогизмов, большую посылку ставят всегда первой, а меньшую – второй. Тогда в зависимости от расположения терминов все простые категорические силлогизмы можно разделить на четыре вида. Эти виды называются фигурами. Фигура – это форма простого категорического силлогизма, которая определяется расположением среднего термина. 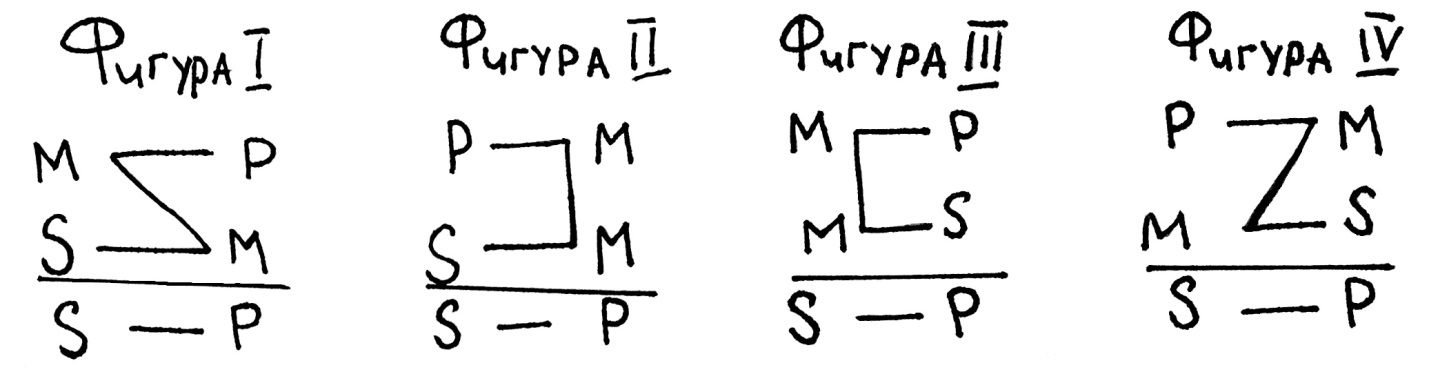 Сверху расположена большая посылка, за ней следует меньшая посылка, под чертой находится заключение. Буквой S обозначен меньший термин, буквой P – больший термин, буквой М – средний термин. Далее, фигуры могут наполняться разным содержанием, то есть на место посылок и заключений могут подставляться разные типы категорических атрибутивных высказываний. Например: Всякий М есть P Всякий S есть М Всякий S есть P или: Ни один М не есть P Некоторые М есть S Некоторые S не есть P Эти различные сочетания высказываний в фигурах образуют так называемые модусы. Каждая фигура имеет 64 модуса, таким образом, на все четыре фигуры приходятся всего 256 модусов. Если подумать обо всём многообразии умозаключений, имеющих форму силлогизмов, то 256 модусов – это не так уж и много. Кроме того, далеко не все модусы образуют правильные умозаключения, то есть существуют такие модусы, которые при истинности посылок не гарантируют истинности умозаключения. Такие модусы называются неправильными. Правильными же называются те модусы, с помощью которых из истинных посылок мы всегда получаем истинное заключение. Всего существует 24 правильных модуса – по шесть на каждую фигуру. Это означает, что во всей классической силлогистике, которая исчерпывает львиную долю рассуждений, производимых людьми, существует всего 24 вида правильных умозаключений. Это очень маленькое число, поэтому правильные модусы не так уж и сложно запомнить. Каждый из этих модусов ещё в Средние века получил особое мнемоническое наименование. Каждый тип категорического атрибутивного высказывания был обозначен с помощью всего одной буквы. Высказывания типа «Все S есть P» обозначили буквой «а», первой буквой в латинском слове «affirmo» («утверждаю»), и их запись превратилась в «SaP». Высказывания вида «Некоторые S есть P» записывались с помощью буквы «i», второй гласной в слове «affirmо», поэтому они выглядели как «SiP». Высказывания формы «Ни один S не есть P» обозначили буквой «е», первой гласной в латинском слове «nego» («отрицаю»), их стали записывать в виде «SeP». Как вы, наверное, уже догадались высказывания типа «Некоторые S не есть P» обозначили буквой «о», второй гласной в слове «nego», их формальная запись выглядела как «SoP». Поэтому модусы правильных силлогизмов традиционно обозначаются именно с помощью этих четырёх букв, которые для удобства запоминания представлены в виде слов. Таблица всех правильных модусов выглядит так:
К примеру, модус второй фигуры Cesare (eae) в развёрнутом виде будет выглядеть так: Ни один P не есть М Все S есть М Ни один S не есть P Хотя 24 модуса – это совсем не много и в таблице можно усмотреть некоторые регулярности (например, для всех фигур верны модусы eao и eio), запомнить её всё равно сложно. К счастью, это совсем и необязательно. Для проверки силлогизмов можно также пользоваться модельными схемами. Только в отличие от тех схем, которые мы строили раньше, на них уже должно присутствовать не два, а три термина: S, P, M. Давайте возьмём модус четвёртой фигуры Bramantip (aai) и проверим его с помощью модельных схем. Всякий P есть М Всякий М есть S Некоторые S есть P Сначала нужно найти такие модельные схемы, при которых обе посылки будут одновременно истинными. Таких схем всего четыре:   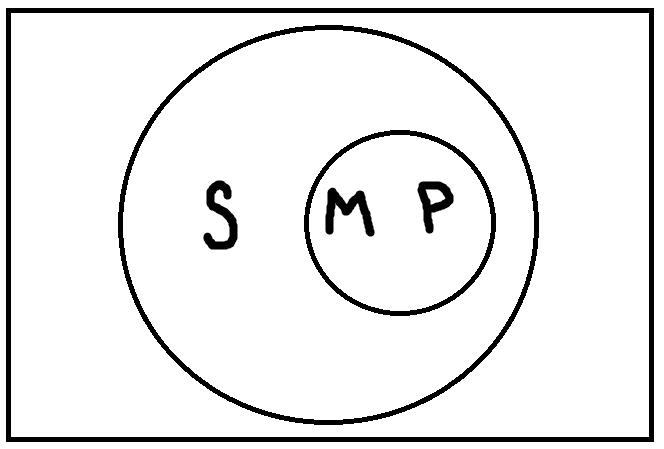 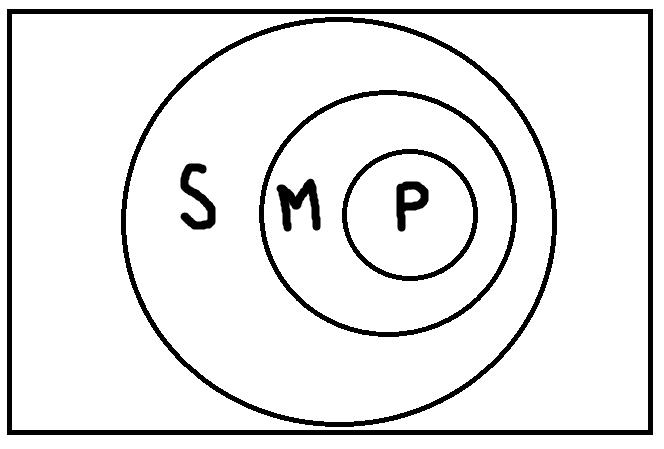 Теперь на каждой из этих схем мы должны проверить, верно ли будет высказывание «Некоторые S есть P», представляющее заключение. В результате проверки, мы обнаруживаем, что на каждой схеме это высказывание будет верным. Таким образом, умозаключение по модусу Bramantip (aai) четвёртой фигуры правильное. Если бы была хотя бы одна схема, на которой это высказывание было бы ложным, то умозаключение было бы неправильным. Метод проверки силлогизмов с помощью модельных схем хорош, так как он позволяет представить отношения между терминами наглядно. Однако для некоторых посылок могут оказаться верными очень много схем сразу. В результате их построение и проверка будут представлять собой трудоёмкую и отнимающую много времени задачу. Таким образом, метод модельных схем не всегда удобен. Поэтому логики разработали ещё один метод для определения, правильный силлогизм или нет. Этот метод называется синтаксическим и представляет собой два перечня правил (правила терминов и правила посылок), при соблюдении которых силлогизм будет верным. Модус простого категорического силлогизма является правильным, если он удовлетворяет следующим условиям: 22) Если индукцию рассматривать как логическую операцию, противоположную дедукции, то суть индуктивного умозаключения состоит в том, что в его результате на основании знания об отдельных предметах данного класса получается общий вывод обо всех предметах данного класса. В процессе индукции от знания меньшей степени общности приходим к новому знанию большей степени общности. В индукции, скажем еще проще, общее заключение выводится из менее общих посылок. При втором подходе, присущем математической логике, индукцией называется умозаключение, дающее вероятностное суждение. В истории физики, например, опытным путем было установлено, что железные стержни хорошо проводят электричество. Такое же свойство было обнаружено у медных и серебряных стержней. Учитывая принадлежность указанных проводников к металлам, было сделано индуктивное обобщение, что всем металлам свойственна электропроводность. Другой пример. Подвергнув экономическому анализу положение дел на предприятиях № 1, № 2, № 3 и т.д., можно сделать индуктивное умозаключение о том, что состояние экономики на большинстве предприятий определенной отрасли улучшается (ухудшается). Виды и формы индукции Существуют две формы индукции: полная и неполная. Полная индукция – это вид, индуктивного умозаключения, в процессе которого делается общий вывод обо всем классе каких-либо предметов на основании знания обо всех без исключения предметах этого класса. Здесь общий вывод получается из ряда суждений, сумма которых полностью исчерпывает все случаи (варианты) данного класса. В итоге то, что утверждается в каждом суждении о каждом отдельном предмете данного класса, в выводе относится ко всем предметам класса. Приведем пример полной индукции: В понедельник на прошлой неделе спрос на акции нашего предприятия был высокий Во вторник................................. тоже В среду....................................... тоже В четверг.................................... тоже В пятницу................................... тоже В субботу................................... тоже В воскресенье............................ тоже Спрос на акции нашего предприятия на прошлой неделе был высокий, т.е. все дни недели спрос на акции был высокий. Посылками индуктивного умозаключения выступают суждения, в которых фиксируется опытным путем информация об устойчивой повторяемости признака Р у ряда явлений S1,S2,… Sп, принадлежащих одному классу К. Схема полной индукции: S1 обладает Р S2 обладает Р S3 обладает Р ………………… Sп обладает Р S1, S2,..., Sn принадлежит к классу К. Каждый элемент К обладает Р. Полную индукцию Аристотель назвал «силлогизмом по индукции». Основанием для вывода по полной индукции могут быть не только единичные, но и общие суждения. Достоинство полной индукции в том, что она дает достоверное заключение. Это требует выполнения следующих условий. Необходимо, во-первых, точно знать число предметов или явлений, которые мы исследуем. Во-вторых, следует убедиться, что свойство принадлежит каждому предмету группы (класса). Количество предметов изучаемой группы – третье условие – должно быть ограничено. Недостаток полной индукции в том, что она не применима в тех случаях, когда исследуются группы предметов или явлений, число элементов которых очень велико, и невозможно дать достоверного заключения о каждом элементе. Допустим, ваше предприятие получило несколько вагонов строительного леса или большую партию яблок, упакованных в ящики. Возможно ли и в первом, и во втором случаях методом полной индукции дать заключение о качестве буквально каждой доски и каждого яблока? Вероятно, нет. Поэтому для получения определенного вывода придется прибегнуть к другому виду индукции – неполной. Неполная индукция – это вид индуктивного умозаключения, в процессе которого делается вывод обо всем классе предметов на основании исследования лишь некоторых однородных предметов данного класса. Например, анализируя случаи дорожно-транспортных происшествий, работники ГАИ констатируют и в одном, и в другом, и в третьем случаях связь аварии с употреблением водителем спиртных напитков. Это дает им основание сделать вывод о том, что употребление спиртных напитков в большинстве случаев является причиной происшествия на дорогах. Наблюдая, как под влиянием спроса колеблются цены на рынке, биржевик делает вывод о том, что цена производна от спроса. Схема неполной индукции: S1 обладает Р S2 обладает Р S3 обладает Р ……………………… Sn обладает Р S1, S2,..., Sn принадлежит к классу К. По-видимому, каждый элемент К обладает Р. Неполную индукцию порой называют расширяющейся, т.к. она в заключении дает больше информации, чем та, которую мы почерпнули из посылок. Ценность ее именно в том и заключается: от некоторого количества фактов мы приходим к выводу, который распространяется и на другие факты. Таким образом, нет необходимости осуществлять перебор всех предметов или явлений. По способам обоснования заключения неполная индукция делится на три вида: |
