Дискретная математика Сборник заданий 2010. 1 Множества и отношения 1 Основные понятия и определения

• Название: 1 Множества и отношения 1 Основные понятия и определения
• Анкор: Дискретная математика Сборник заданий 2010
• Дата: 12.02.2022
• Размер: 1.67 Mb.
• Имя файла: Дискретная математика Сборник заданий 2010 .doc
• Тип: Документы; #359373
• страница: 3 из 8

1.3 Примеры выполнения заданий

Задание 1

Пример 1: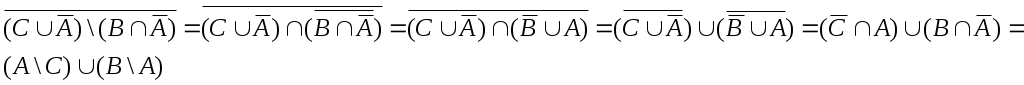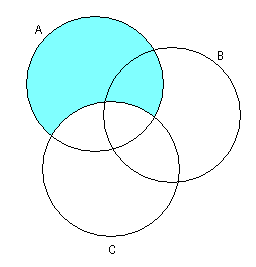

1)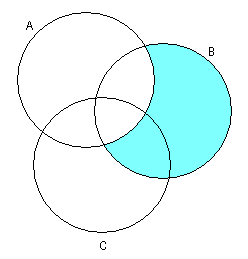



2)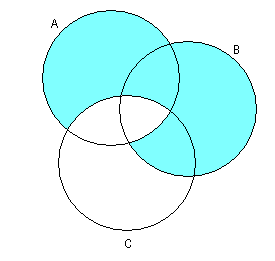


3)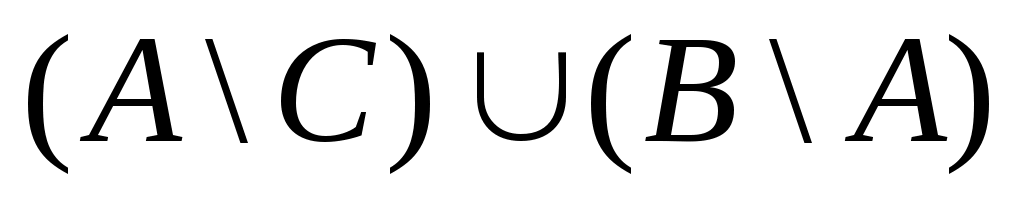

Пример 2: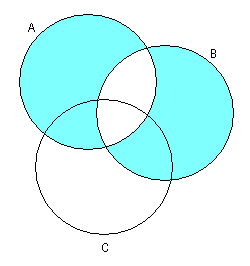

1)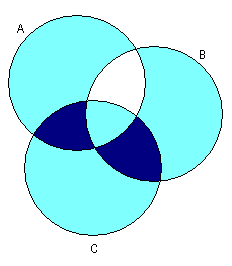



2)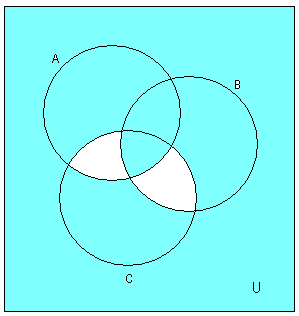


3)

Задание 2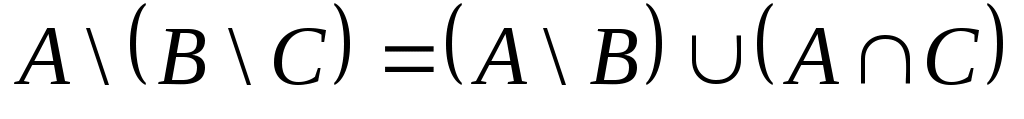

Покажем выполнение равенства на диаграммах Эйлера-Венна.

1) Левая часть равенства: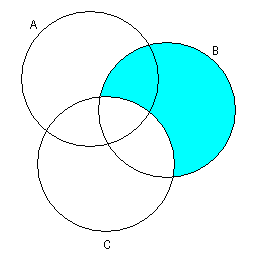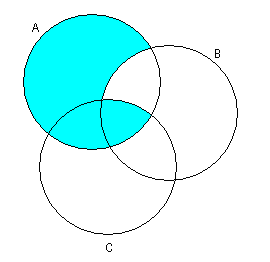

2) Правая часть равенства: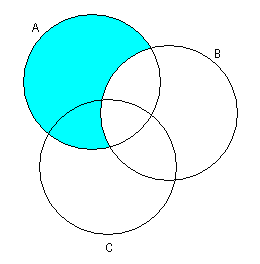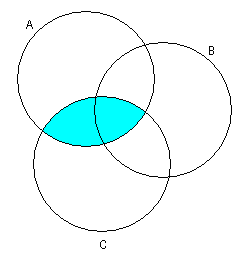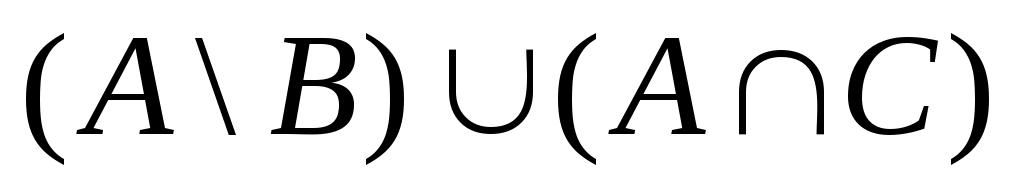

Докажем при помощи тождеств алгебры множеств: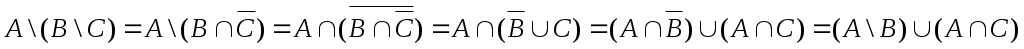

Задание 3

в) Из а) и б) выполнение равенства.

Задание 4

Схематично изобразить геометрическое место точек прямого произведения {1,2,3,4}×{xx-точка квадрата}.

Геометрическое место точек прямого произведения множеств {1,2,3,4}×{xx-точка квадрата} изображено на рисунке.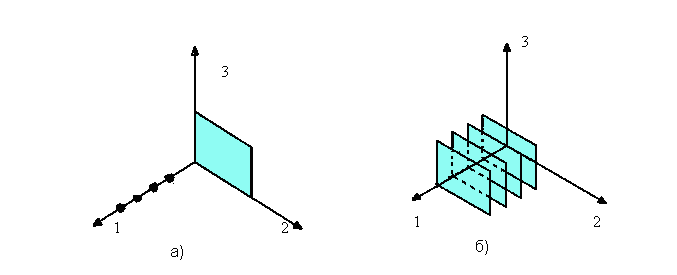



На рисунке а) на оси 1 изображены точки множества {1,2,3,4}; на плоскости 2О3 – множество точек квадрата: {xx-точка квадрата}.

На рисунке б) изображен результат.

Задание 5

Отношения 1 и 2 заданы на множестве натуральных чисел.

1-"x и y кратны 100"; 2-"x и y кратны 2".

Вычислить:

1 4

2 5

3 6

Решение:

1={<100,100>,<100,200>,<200,300>,…,<100*i,100*i>},где iN

2={<2,2>,<2,4>,<4,2>,…,<2*i,2*i>},где iN.

Для наглядности изобразим множества 1 и 2 на диаграмме Эйлера-Венна (см. рисунок). Все элементы множества 1 находятся среди элементов множества 2, следовательно 1 2.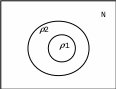



1. 1Uр2=2.

2. 1∩2=1.

3. 1\2=.

4. 1+2=(1\2)U(2\1)=U(2\1)=(2\1)= {<2,2>,<2,4>,<4,2>,…,<2*i,2*i>}\{<100,100>,<100,200>,<200,300>,…,<100*i,100*i>}={-"x и y кратны 2 и x и y некратны 100"}, где iN.

5. По определению композиции отношений:

1◦2={ y 1, 2}={"x кратно 2, z кратно 100"}.

6. R1={100,200,300,…,100*i}, R2={2,4,6,…,2*i}, где iN, следовательно R1R2.

Задание 6

,
a) = {<1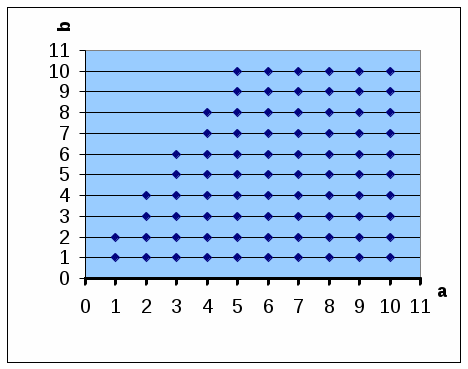,1>, <1,2>, <2,1>, <2,2>, <2,3>, <3,1>, <3,6>, <4,3>, ...}

b)



c) Несимметрично, т.к. для пары <3,1> не существует пары <1,3>;

Рефлексивно, т.к. для найдется пара . Например, <1,1>, <2,2>, <3,3> и т.д.;

Не транзитивно, т.к. для пар <1,2> ,<2,3> не существует пары <1,3>;

Не антисимметрично, т.к. есть пары <1,2>, <2,1> и при этом 1 2.

Задание 7

«Быть подмножеством» на семействе множеств
антисимметрично, т.к. из того, что , а следует, что ;

несимметрично, т.к. из того что , не следует, что ;

рефлексивно, т.к. любое множество ;

транзитивно, т.к. из того, что , а следует, что .

Задание 8

Отношение f является функцией, т.к. каждому значению x соответствует единственное значение y.

Отношение f не является инъективным, т.к. значению y соответствуют два значения x. Например, y=5, x1=0, x2= -3.

Отношение f не является сюръективным, т.к. не существует x для отрицательных значений y.

Отношение является отображением, т.к. можно рассчитать y для всех x из множества R.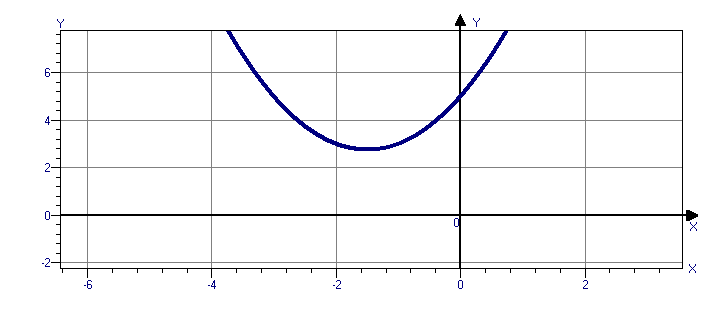