Дискретная математика Сборник заданий 2010. 1 Множества и отношения 1 Основные понятия и определения

• Название: 1 Множества и отношения 1 Основные понятия и определения
• Анкор: Дискретная математика Сборник заданий 2010
• Дата: 12.02.2022
• Размер: 1.67 Mb.
• Имя файла: Дискретная математика Сборник заданий 2010 .doc
• Тип: Документы; #359373
• страница: 1 из 8

1 Множества и отношения

1.1 Основные понятия и определения

• 
  Под множеством понимается совокупность определенных и различимых между собой объектов, эти объекты называются элементами множества.
  
• 
  Объединением множеств и называется множество:
  

• 
  Пересечением множеств и называется множество:
  

• 
  Разностью множеств и называется множество:
  

• 
  Универсальное множество - множество, для которого в ходе какого-либо рассуждения все множества являются подмножествами.
  
• 
  Дополнение (до ) множества :
  
• 
  Симметрическая разность множеств 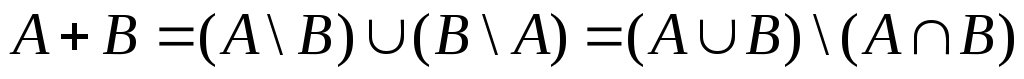и :
  

• 
  Прямым произведением множеств и называется множество :
  

• 
  Бинарным (двуместным) отношением называется множество упорядоченных пар или
  
• 
  Обратное отношение
  
• 
  Композиция отношений
  
• 
  Отображением в называется всюду определенное соответствие, такое что , т.е.
  
• 
  Функцией называется бинарное отношение, обладающее свойством для любых пар .
  
• 
  Функция называется инъективной, если для любого .
  
• 
  Функция называется сюръективной, если для любого .
  
• 
  Функция называется биективной, если f инъективна и сюръективна.
  

Специальные бинарные отношения

• 
  Отношение на множестве Х называется рефлексивным, если выполняется .
  
• 
  Отношение на множестве Х называется симметричным, если из того, что следует, что .
  
• 
  Отношение на множестве Х называется транзитивным, если из того, что и .
  
• 
  Отношение на множестве Х называется антисимметричным, если из того, что и .
  
• 
  Отношение частичного порядка – рефлексивное, антисимметричное, транзитивное.
  
• 
  Отношение линейного порядка – это отношение частичного порядка, у которого любые два элемента сравнимы.
  
• 
  Отношение эквивалентности – рефлексивное, симметричное, транзитивное.
  
• 
  Отношение сравнимости по модулю z на множестве M: ={| x,yM, y=xkz, k=0,1,...}.
  
• 
  Класс эквивалентности, порожденный элементом x: x={yM| xy}, - отношение эквивалентности на множестве M.