Дискретная математика Сборник заданий 2010. 1 Множества и отношения 1 Основные понятия и определения

• Название: 1 Множества и отношения 1 Основные понятия и определения
• Анкор: Дискретная математика Сборник заданий 2010
• Дата: 12.02.2022
• Размер: 1.67 Mb.
• Имя файла: Дискретная математика Сборник заданий 2010 .doc
• Тип: Документы; #359373
• страница: 7 из 8

2.3 Примеры выполнения заданий

Задание 1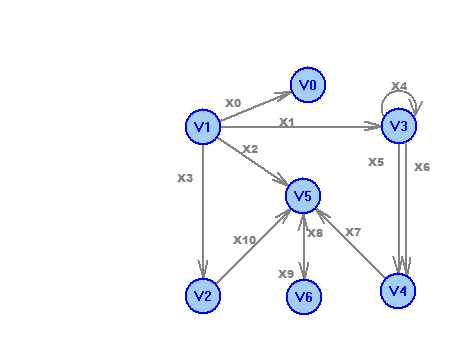

1. 
   Ориентированный псевдограф D=(V,X). V={v₀,v₁,v₂,v₃,v₄,v₅,v₆}, X={x₀,x₁,x₂,x₃,x₄,x₅,x_6,x₇,x₈,x₉,x₁₀}. x₀=1,v₀>, x₁=1,v₃>, x₂=1,v₅>, x₃=1,v₂>, x₄=3,v₃>, x₅=3,v₄>, x₆=3,v₄>, x₇=4,v₅>, x₈=6,v₅>, x₉=5,v₆>, x₁₀=2,v₅>.
   

2. 
   x₄ – петля, x₅,x₆ – кратные ребра, v₀ – висячая вершина.
   

3. 
   Полустепени вершин: ⁺(v₀)=0, ^-(v₀)=1, ⁺(v₁)=4, ^-(v₁)=0, ⁺(v₂)=1, ^-(v₂)=1, ⁺(v₃)=3, ^-(v₃)=2, ⁺(v₄)=1, ^-(v₄)=2, ⁺(v₅)=1, ^-(v₅)=4, ⁺(v₆)=1, ^-(v₆)=1.
   

4. 
   
   

Матрица смежности

	v0	v1	v2	v3	v4	v5	v6
v0	0	0	0	0	0	0	0
v1	1	0	1	1	0	1	0
v2	0	0	0	0	0	1	0
v3	0	0	0	1	2	0	0
v4	0	0	0	0	0	1	0
v5	0	0	0	0	0	0	1
v6	0	0	0	0	0	1	0

Матрица инцидентности

	x0	x1	x2	x3	х4	х5	х6	х7	x8	x9	x10
v0	-1	0	0	0	0	0	0	0	0	0	0
v1	1	1	1	1	0	0	0	0	0	0	0
v2	0	0	0	-1	0	0	0	0	0	0	1
v3	0	-1	0	0	±1	1	1	0	0	0	0
v4	0	0	0	0	0	-1	-1	1	0	0	0
v5	0	0	-1	0	0	0	0	-1	-1	1	-1
v6	0	0	0	0	0	0	0	0	1	-1	0

Матрица связности:

	v0	v1	v2	v3	v4	v5	v6
v0	1	0	0	0	0	0	0
v1	0	1	0	0	0	0	0
v2	0	0	1	0	0	0	0
v3	0	0	0	1	0	0	0
v4	0	0	0	0	1	0	0
v5	0	0	0	0	0	1	1
v6	0	0	0	0	0	1	1

Матрица достижимости:

	v0	v1	v2	v3	v4	v5	v6
v0	1	0	0	0	0	0	0
v1	1	1	1	1	1	1	1
v2	0	0	1	0	0	1	1
v3	0	0	0	1	1	1	1
v4	0	0	0	0	1	1	1
v5	0	0	0	0	0	1	1
v6	0	0	0	0	0	1	1

5. 
   Простой цикл: v₆х₈v₅х₉v₆
   

Цикл: нет

Простая цепь : v₁х₃v₂х₁₀v₅

Цепь: v₁х₁v₃х₄v₃х₆v₄

Задание 2

Матрица длин дуг

	v0	v1	v2	v3	v4	v5
v0	∞	3	5	∞	8	3
v1	3	∞	2	6	7	∞
v2	5	2	∞	∞	4	∞
v3	∞	6	∞	∞	5	∞
v4	8	7	4	5	∞	∞
v5	3	∞	∞	∞	∞	∞

1. 
   
   

2. 
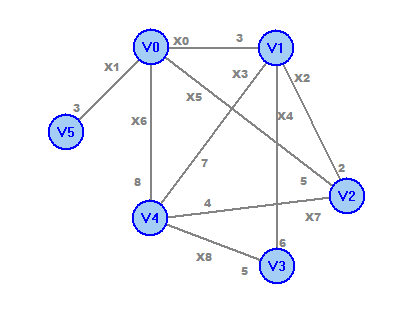   Неориентированный граф G=(V,X). V={v₀,v₁,v₂,v₃,v₄,v₅}, X={x₀,x₁,x₂,x_3,x₄,x₅,x_6,x₇,x₈}. x₀={v₀,v₁}, x₁={v₀,v₅}, x₂={v₁,v₂}, x₃={v₁,v₄}, x₄={v₁,v₃}, x₅={v₀,v₂}, x₆={v₀,v₄}, x₇={v₂,v₄}, x₈={v₃,v₄}.
   

3. 
   v₅ – висячая вершина.
   

4. 
   (v₀)=4, (v₁)=4, (v₂)=3, (v₃)=2, (v₄)=4, (v₅)=1.
   

http://graphonline.ru/?graph=DqpDaEgcctWYgpgl

5. 
   
   

Матрица смежности

	v0	v1	v2	v3	v4	v5
v0	0	1	1	0	1	1
v1	1	0	1	1	1	0
v2	1	1	0	0	1	0
v3	0	1	0	0	1	0
v4	1	1	1	1	0	0
v5	1	0	0	0	0	0

Матрица инцидентности

	x0	x1	x2	x3	х4	х5	х6	х7	x8
v0	1	1	0	0	0	1	1	0	0
v1	1	0	1	1	1	0	0	0	0
v2	0	0	1	0	0	1	0	1	0
v3	0	0	0	0	0	0	0	1	1
v4	0	0	0	1	0	0	1	1	1
v5	0	1	0	0	0	0	0	0	0

Матрица связности:

	v0	v1	v2	v3	v4	v5
v0	1	1	1	1	1	1
v1	1	1	1	1	1	1
v2	1	1	1	1	1	1
v3	1	1	1	1	1	1
v4	1	1	1	1	1	1
v5	1	1	1	1	1	1

Матрица достижимости:

	v0	v1	v2	v3	v4	v5
v0	1	1	1	1	1	1
v1	1	1	1	1	1	1
v2	1	1	1	1	1	1
v3	1	1	1	1	1	1
v4	1	1	1	1	1	1
v5	1	1	1	1	1	1

6. 
   Простой цикл: v₀х₀v₁х₂v₂х₅v₀
   

Цикл: v₄x₆v₀x₅v₂x₇v₄x₃v₁x₄v₃х₈v₄

Простая цепь: v₂х₅v₀х₁v₅

Цепь: v₀х₀v₁х₂v₂х₇v₄х₃v₁х₄v₃

7. 
   Числовые характеристики
   

a) Максимальное удаление – r(v) = max_wd(v,w)

r(v₀)=2, r(v₁)=2, r(v₂)=2, r(v₃)=3, r(v₄)=2, r(v₅)=3

б) Диаметр графа d(G)=max_v,wd(v,w)

d(G)=3

в) Радиус графа G- r(G)=min_v r(v)

R(G)=2

г) Центры графа-v| R(G)=r(v)

центры графа - вершины v₀, v₁, v_2, v₄.

8. 
   
   

Рассчитаем остовное дерево графа: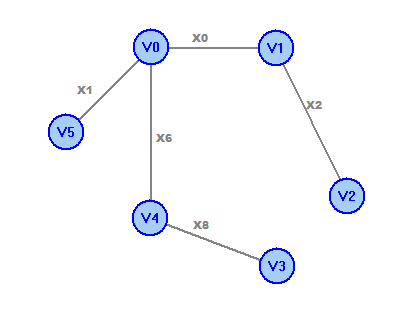


Рассчитаем минимальное остовное дерево графа: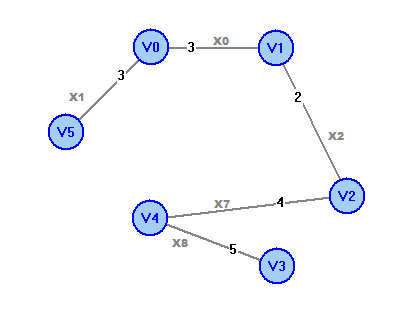

9. 
   Обход графа в глубину: v0v1v2v4v3v5.
   

Обход графа в ширину. 1 ярус: v0; 2 ярус: v1,v2,v4,v5; 3 ярус: v3.

10. 
    Число циклов в базисе (цикломатическое число графа)
    

.

Чтобы найти базис циклов графа, к остовному дереву будем добавлять по одному ребра, которые в остовное дерево не вошли. При этом на каждом шаге будем получать один простой цикл.

Добавим ребро x₃: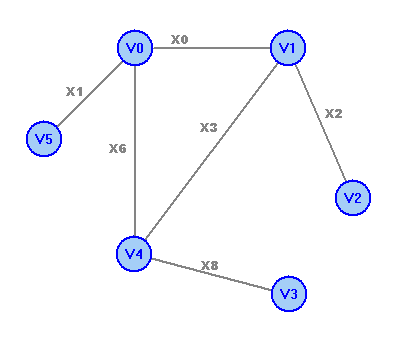



Получим цикл 1: v₄x₆v₀x₀v₁x₃v₄.

Добавим ребро x₄: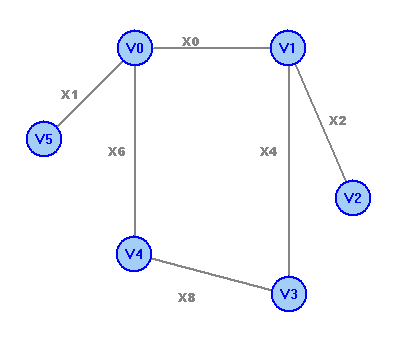



Получим цикл 2: v₃x₈v₄x₆v₀x₀v₁x₄v₃.

Добавим ребро x₅: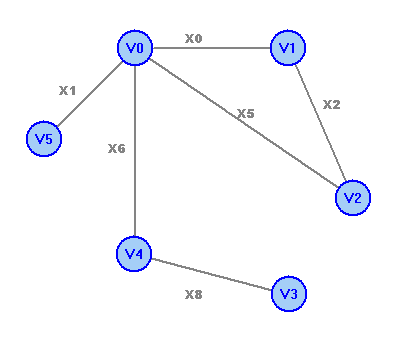



Получим цикл 3: v₀x₀v₁x₂v₂x₅v₀.

Добавим ребро x₇: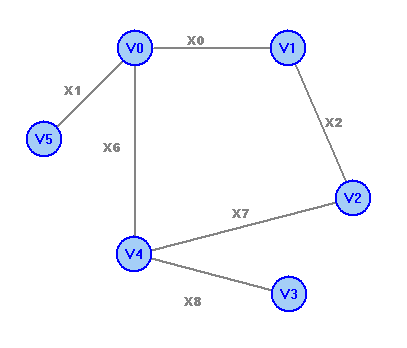



Получим цикл 4: v₄x₆v₀x₀v₁x₂v₂x₇v₄

Полученные циклы и образуют базис циклов графа.