Дискретная математика Сборник заданий 2010. 1 Множества и отношения 1 Основные понятия и определения

• Название: 1 Множества и отношения 1 Основные понятия и определения
• Анкор: Дискретная математика Сборник заданий 2010
• Дата: 12.02.2022
• Размер: 1.67 Mb.
• Имя файла: Дискретная математика Сборник заданий 2010 .doc
• Тип: Документы; #359373
• страница: 4 из 8

2 Теория графов

2.1 Основные понятия и определения

• 
  Граф – пара множеств V и X - G = (V,X). V – множество вершин, X – множество ребер.
  
• 
  Петля – ребро вида (v,v).
  
• 
  Кратные рёбра – одинаковые пары в X.
  
• 
  Ориентированный граф (орграф D) – граф, для которого пары в Х упорядочены. Ребра в орграфе называются дугами и обозначаются .
  
• 
  Степенью вершины V графа G называется число (v) рёбер графа, инцидентных вершине v. Если (v) = 1, тогда v – висячая вершина, если (v) = 0, тогда v –изолированная вершина.
  
• 
  Полустепенью исхода (захода) вершины v орграфа D называется ⁺(v) – число дуг, исходящих из v (δ^- (v)- число дуг, заходящих в v).
  
• 
  Маршрутом для графа G (путём для орграфа D) называется последовательность v₁x₁v₂x₂v₃. . .x_kv_k+1.
  
• 
  Цепь – незамкнутый маршрут (путь), в котором все рёбра (дуги) попарно различны.
  
• 
  Простая цепь – цепь, в которой все вершины попарно различны.
  
• 
  Цикл (контур) - замкнутый маршрут (путь), в котором все рёбра (дуги) попарно различны.
  
• 
  Простой цикл (контур) - цикл (контур), в котором все вершины попарно различны.
  
• 
  Длина пути – число рёбер (дуг) в маршруте (пути).
  
• 
  Путь в графе называется минимальным, если он состоит из минимального количества рёбер.
  
• 
  Орграф D называется нагруженным, если на множестве дуг Х определена весовая функция – длина дуги хХ.
  
• 
  Путь называется минимальным в нагруженном графе или орграфе, если он имеет минимальную длину пути.
  
• 
  Матрица смежности (графа, орграфа): А = [a_ij], V = {v₁…,v_n},
  
• 
  X = {x₁…,x_m}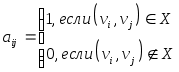
  
• 
  
  
• 
  Матрица инцидентности: B = [b_ij]
  
• 
  (орграфа D)
  
• 
  
  

• 
  (графа G)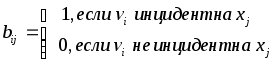
  
• 
  
  

• 
  Матрица достижимости T = [t_ij]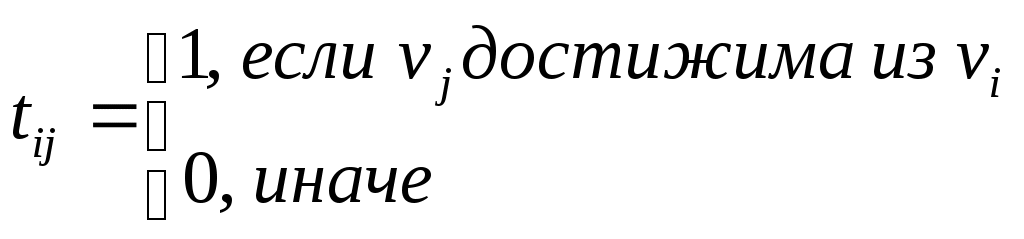
  
• 
  
  

• 
  Матрица связности S = [s_ij]
  
• 
  (орграфа D)
  

• 
  (графа G)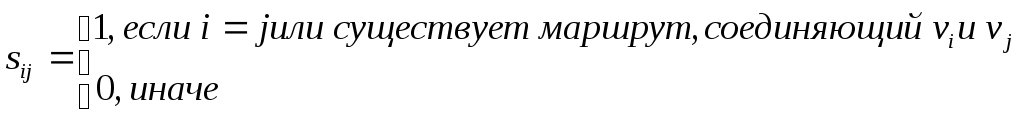
  

• 
  Дерево – связный граф без циклов
  
• 
  Остовное дерево графа (ОД) – любой связный подграф связного графа, содержащий все вершины и являющийся деревом.
  

Минимальное остовное дерево (МОД) – остовное дерево нагруженного графа с минимальной суммой длин дуг, содержащихся в нём.

• 
  Цикломатическое число связного графа G (число циклов в базисе циклов графа) , где n – количество вершин, m – количество ребер в графе.
  

2.2 Задания

Задание 1. Ориентированный граф

1. 
   Охарактеризовать граф.
   
2. 
   Назвать специальные вершины и рёбра.
   
3. 
   Рассчитать полустепени вершин.
   
4. 
   Выписать матрицы смежности, инцидентности, достижимости, связности.
   
5. 
   Выписать цикл, цепь, простой цикл, простую цепь.
   

1.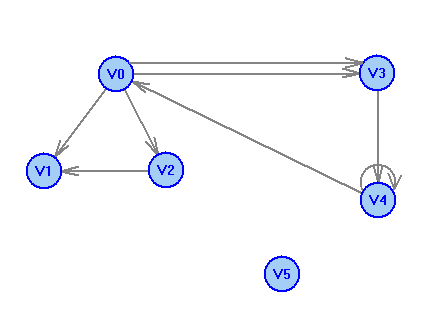


2.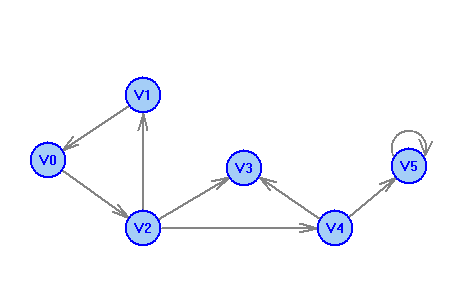


3.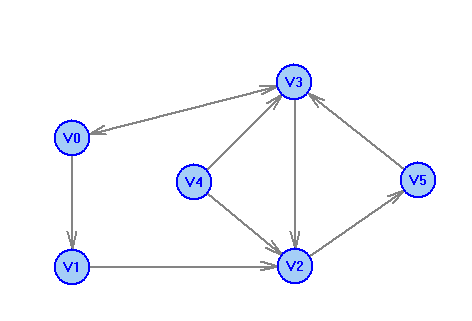


4.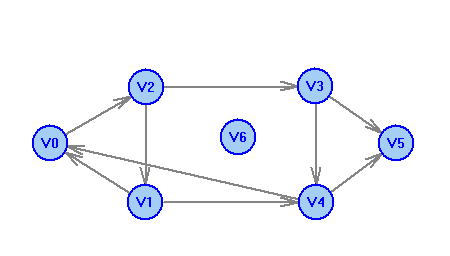



5.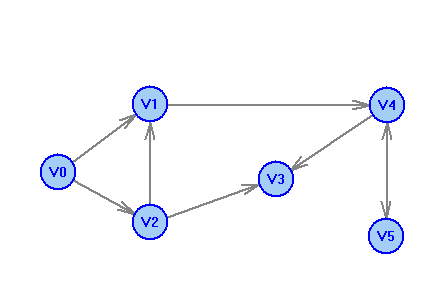


6.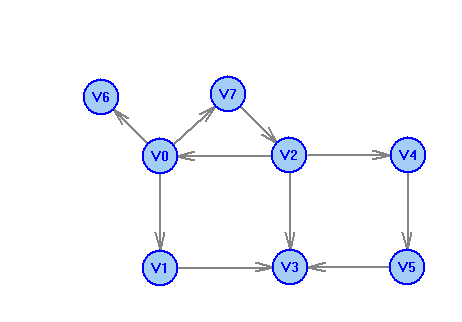


7.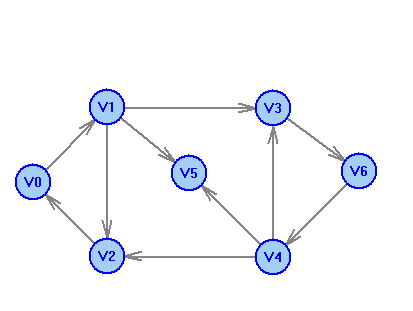


8.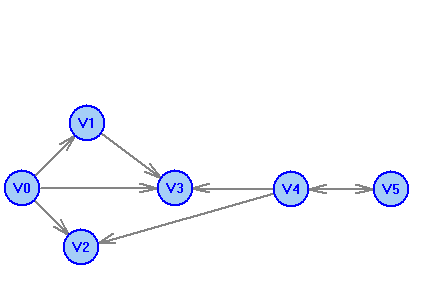



9.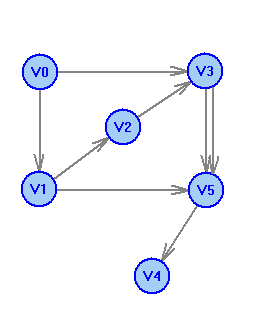


10.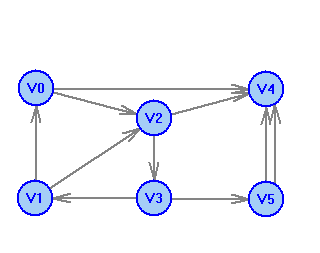


11.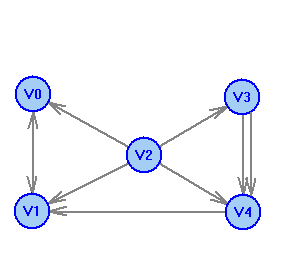


12.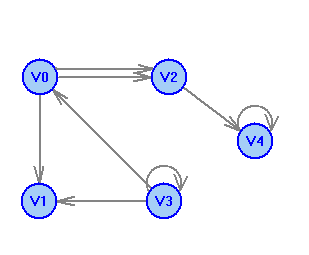


13.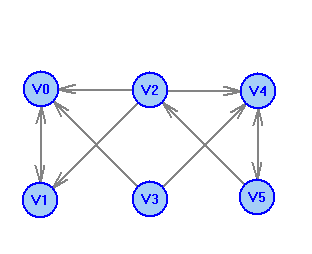



14.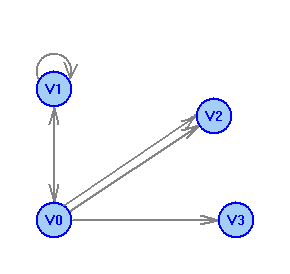



15.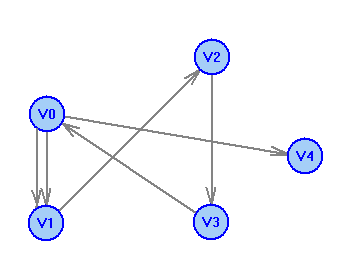


16.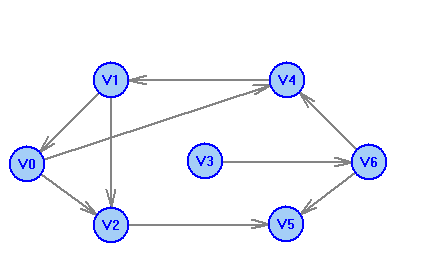


17.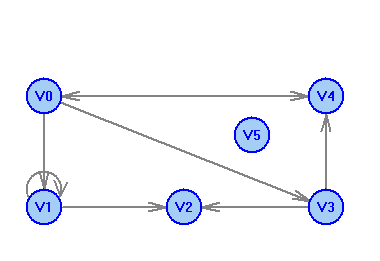



18.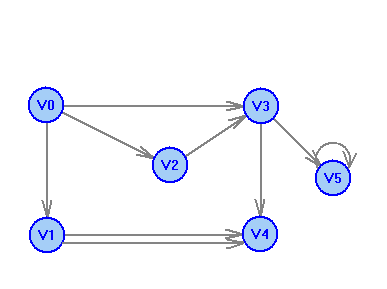



19.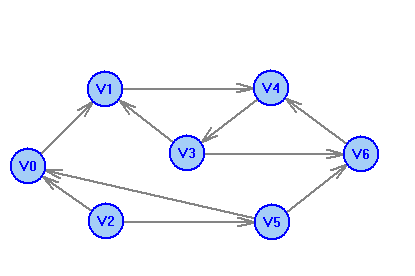


20.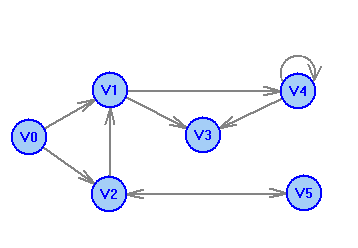



21.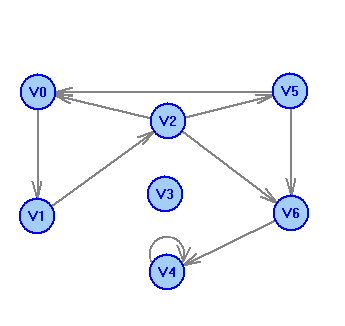


22.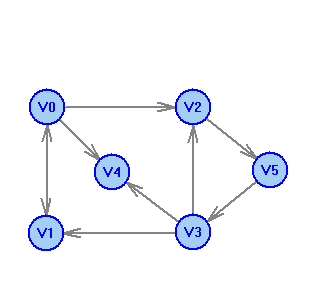



23.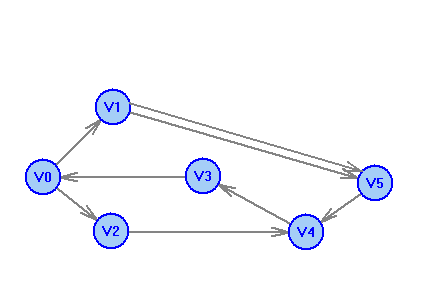



24.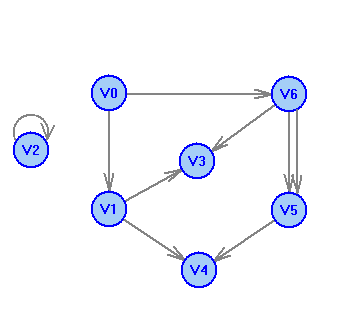


25.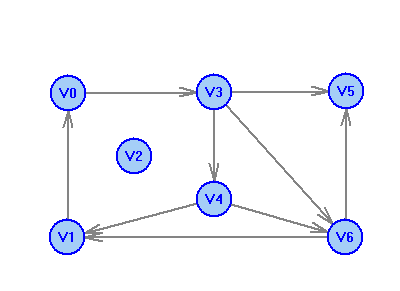


26.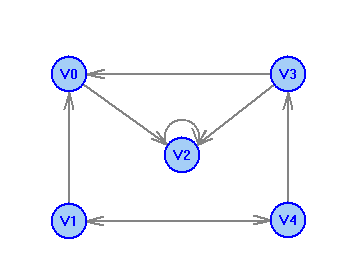



27.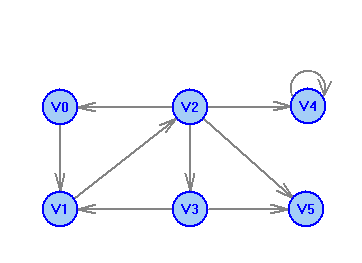


28.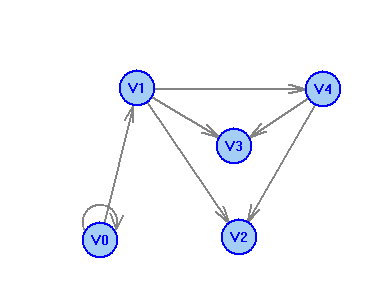


29.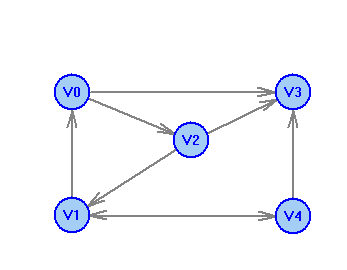


30.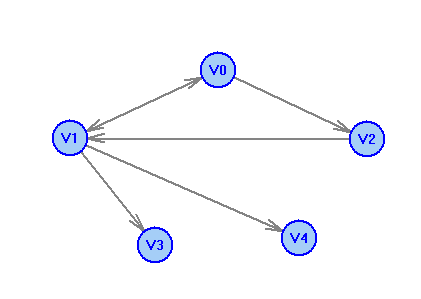