Лаораторная 1. 1. моделирование как метод исследования содержание, цели и задачи учебной дисциплины Предметная область дисциплины
 Скачать 0.9 Mb.
|
|
Качественные и количественные модели Задача науки состоит в построении теоретической модели окружающего мира, которая бы объясняла известные и предсказывала неизвестные явления. Теоретическая модель может быть качественной или количественной. Рассмотрим качественное объяснение электромагнитных колебаний в колебательном контуре, состоящем из конденсатора и катушки индуктивности. При подключении заряженного конденсатора к катушке индуктивности он начинает разряжаться, через катушку индуктивности течет ток, энергия электрического поля переходит в энергию магнитного поля. Когда конденсатор полностью разрядился, ток через катушку индуктивности достигает максимального значения. За счет инерционности катушки индуктивности, обусловленной явлением самоиндукции, происходит перезарядка конденсатора, он заряжается в обратном направлении и т.д. Эта качественная модель явления позволяет проанализировать поведение системы и предсказать, например, что при уменьшении емкости конденсатора частота собственных колебаний контура возрастет. Важным шагом на пути познания является переход от качественно–описательных методов к математическим абстракциям. Решение многих проблем естествознания потребовало оцифровки пространства и времени, введения понятия системы координат, разработки и совершенствования методов измерения различных физических, психологических и иных величин, что позволило оперировать с численными значениями. В результате были получены достаточно сложные математические модели, представляющие систему алгебраических и дифференциальных уравнений. В настоящее время исследование природных и иных явлений уже не ограничивается качественными рассуждениями, а предусматривает построение математической теории. Создание количественноймодели электромагнитных колебаний в RLC-цепи предполагает введение точных и однозначных способов определения и измерения таких величин, как сила тока  , заряд  , напряжение  , емкость  , индуктивность  , сопротивление  . Не зная, как измерить силу тока в цепи или емкость конденсатора, бессмысленно говорить о каких–то количественных соотношениях. Имея однозначные определения перечисленных величин, и установив процедуру их измерения, можно приступать к построению математической модели, записи системы уравнений. В результате получается неоднородное дифференциальное уравнение второго порядка  . Его решение позволяет, зная заряд конденсатора и ток через катушку индуктивности в начальный момент, определить состояние цепи в последующие моменты времени.Построение математической модели требует определения независимых величин, однозначно описывающих состояниеисследуемого объекта. Например, состояние механической системы определяется координатами входящих в нее частиц и проекциями их импульсов. Состояние электрической цепи задается зарядом конденсатора, силой тока через катушку индуктивности и т.д. Состояние экономической системы определяется набором таких показателей, как количество денежных средств, вложенных в производство, прибыль, число рабочих, занятых изготовлением продукции и т.д. Поведение объекта во многом определяется его параметрами, то есть величинами, которые характеризуют его свойства. Так, параметрами пружинного маятника являются жесткость пружины и масса подвешенного к ней тела. Электрическая RLC–цепь характеризуется сопротивлением резистора, емкостью конденсатора, индуктивностью катушки. К параметрам биологической системы относятся коэффициент размножения, количество биомассы, потребляемой одним организмом и т.д. Другим важным фактором, влияющим на поведение объекта, является внешнее воздействие. Очевидно, что поведение механической системы зависит от действующих на нее внешних сил. На процессы в электрической цепи влияет приложенное напряжение, а развитие производства связано с внешней экономической ситуацией в стране. Таким образом, поведение исследуемого объекта (а значит и его модели) зависит от его параметров, начального состояния и внешнего воздействия. Создание математической модели требует определения совокупности состояний системы, множества внешних воздействий (входных сигналов) и откликов (выходных сигналов), а также задания соотношений, связывающих отклик системы с воздействием и ее внутренним состоянием. Они позволяют исследовать огромное количество различных ситуаций, задавая иные параметры системы, начальные условия и внешние воздействия. Искомая функция, характеризующая отклик системы, получается в табличном или графическом виде. Все существующие способы исследования математической модели можно разделить на две группы.Аналитическое решение уравнения часто предусматривает проведение громоздких и сложных математических выкладок и в результате приводит к уравнению, выражающему функциональную связь между искомой величиной, параметрами системы, внешним воздействием и временем. Результаты такого решения нуждаются в интерпретации, предполагающей анализ полученных функций, построение графиков. Численные методы исследования математической модели на ЭВМ предполагают создание компьютерной программы, которая решает систему соответствующих уравнений и выводит на экран таблицу либо графическое изображение. Получающиеся статические и динамические картинки наглядно пояснять сущность исследуемых процессов. Компьютерное моделирование Эффективным способом изучения явлений окружающей действительности является научный эксперимент, состоящий в воспроизведении изучаемого явления природы в управляемых и контролируемых условиях. Однако часто проведение эксперимента невозможно либо требует слишком больших экономических затрат и может привести к нежелательным последствиям. В этом случае исследуемый объект заменяют компьютерной моделью и исследуют ее поведение при различных внешних воздействиях. Повсеместное распространение персональных компьютеров, информационных технологий, создание мощных суперЭВМ сделало компьютерное моделирование одним из результативных методов изучения физических, технических, биологических, экономических и иных систем. Часто компьютерные модели проще и удобнее исследовать, они позволяют проводить вычислительные эксперименты, реальная постановка которых затруднена или может дать непредсказуемый результат. Логичность и формализованность компьютерных моделей позволяет выявить основные факторы, определяющие свойства изучаемых объектов, исследовать отклик физической системы на изменения ее параметров и начальных условий. Компьютерное моделирование требует абстрагирования от конкретной природы явлений, построения сначала качественной, а затем и количественной модели. За этим следует проведение серии вычислительных экспериментов на компьютере, интерпретация результатов, сопоставление результатов моделирования с поведением исследуемого объекта, последующее уточнение модели и т.д. Вычислительный эксперимент фактически является экспериментом над математической моделью исследуемого объекта, проводимого с помощью ЭВМ. Часто он значительно дешевле и доступнее натурного эксперимента, его выполнение требует меньшего времени, он дает более подробную информацию о величинах, характеризующих состояние системы. Сущность компьютерного моделирования системы заключается в создании компьютерной программы (пакета программ), описывающей поведение элементов исследуемой системы в процессе ее функционирования, учитывающей их взаимодействие между собой и внешней средой, и проведении на ЭВМ серии вычислительных экспериментов. Это делается с целью изучения природы и поведения объекта, его оптимизации и структурного развития, прогнозирования новых явлений. Перечислим требования, которым должна удовлетворять модель исследуемой системы: 1. Полнота модели, то есть возможность вычисления всех характеристик системы с требуемой точностью и достоверностью. 2. Гибкость модели, что позволяет воспроизводить и проигрывать различные ситуации и процессы, изменять структуру, алгоритмы и параметры изучаемой системы. 3. Длительность разработки и реализации, характеризующая временные затраты на создание модели. 4. Блочность структуры, допускающая добавление, исключение и замену некоторых частей (блоков) модели. Кроме того, информационное обеспечение, программные и технические средства должны позволять модели обмениваться информацией с соответствующей базой данных и обеспечивать эффективную машинную реализацию и удобную работу пользователя. К основным этапам компьютерного моделирования относятся (рис. 3): 1) постановка задачи, описание исследуемой системы и выявление ее компонентов и элементарных актов взаимодействия; 2) формализация, то есть создание математической модели, представляющей собой систему уравнений и отражающей сущность исследуемого объекта; 3) разработка алгоритма, реализация которого позволит решить поставленную задачу; 4) написание программы на конкретном языке программирования; 5)планирование и выполнение вычислений на ЭВМ, доработка программы и получение результатов; 6) анализ и интерпретация результатов, их сопоставление с эмпирическими данными. Затем все это повторяется на следующем уровне. Разработка компьютерной модели объекта представляет собой последовательность итераций: сначала на основе имеющейся информации о системе S строится модель 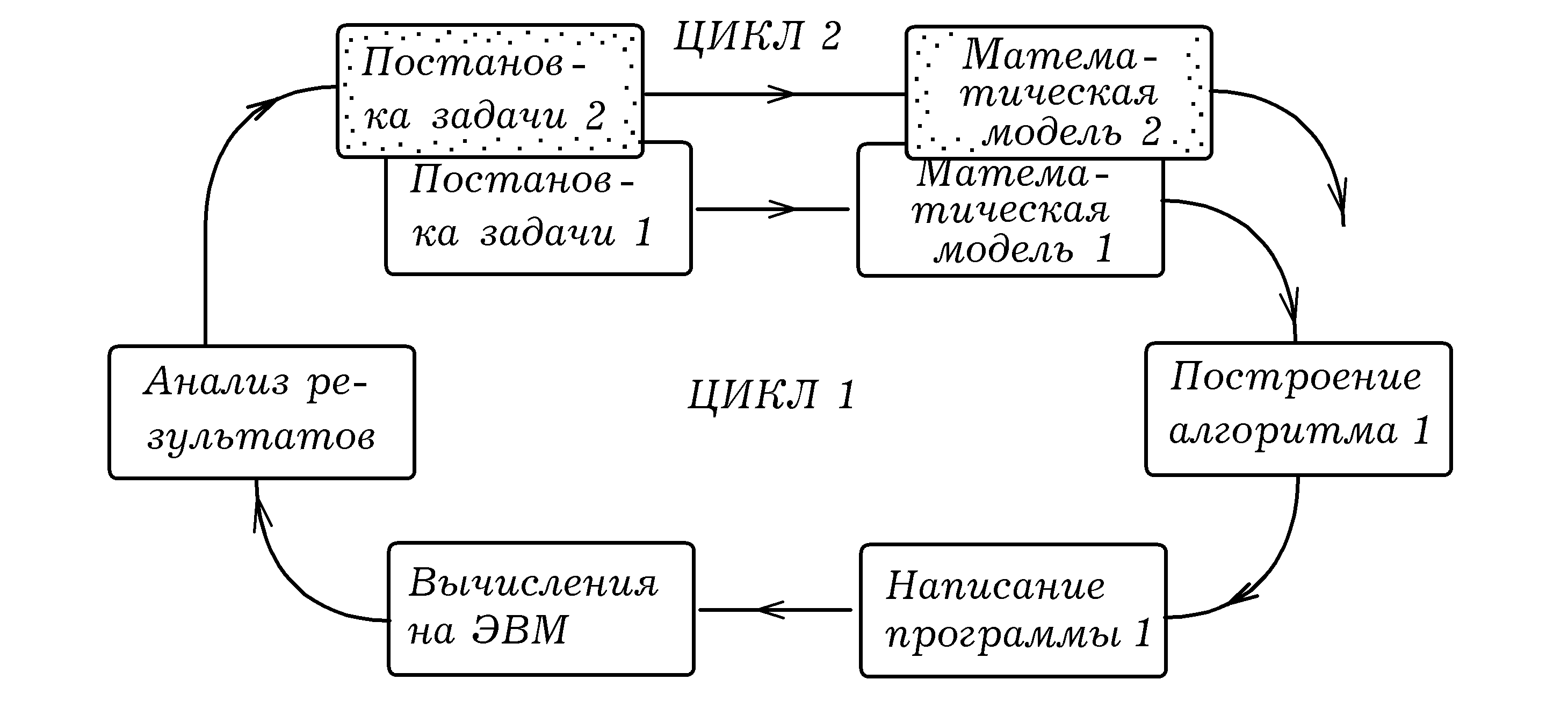 , проводится серия вычислительных экспериментов, результаты анализируются. При получении новой информации об объекте S учитываются дополнительные факторы, получается модель  , поведение которой тоже исследуется на ЭВМ. После этого создаются модели  ,  и т.д. до тех пор, пока не получится модель, с требуемой точностью соответствующая системе S. Рис. 3. Этапы компьютерного моделирования. В общем случае поведение исследуемой системы  описывается законом функционирования  , где  –– вектор входных воздействий (стимулов),  –– вектор выходных сигналов (откликов, реакций),  –– вектор воздействий внешней среды,  –– вектор собственных параметров системы [9]. Закон функционирования может иметь вид словесного правила, таблицы, алгоритма, функции, совокупности логических условий и т.д. В случае, когда закон функционирования содержит время, говорят о динамических моделях и системах. Например, разгон и торможение асинхронного двигателя, переходный процесс в цепи, содержащей конденсатор, функционирование вычислительной сети, системы массового обслуживания. Во всех этих случаях состояние системы, а значит и ее модели, изменяется с течением времени.Если поведение системы описывается законом  , не содержащим время  явно, то речь идет о статических моделях и системах, решении стационарных задач и т.д. Приведем несколько примеров: расчет нелинейной цепи постоянного тока, нахождение стационарного распределения температуры в стержне при постоянных температурах его концов, формы упругой пленки, натянутой на каркас, профиля скоростей в установившемся течении вязкой жидкости и т.д.Функционирование системы можно рассматривать как последовательную смену состояний  ,  , … ,  , которым соответствуют некоторые точки в многомерном фазовом пространстве. Множество всех точек  , отвечающих всевозможным состояниям системы, называют пространством состояний объекта (или модели). Каждой реализации процесса соответствует одна фазовая траектория, проходящая через некоторые точки из множества  . Если математическая модель содержит элемент случайности, то получается стохастическая компьютерная модель. В частном случае, когда параметры системы и внешние воздействия однозначно определяют выходные сигналы, говорят о детерминированной модели.Принципы компьютерного моделирования. Связь c другими методами познания Итак,модель –– это объект, заменяющий исследуемую систему, и имитирующий ее структуру и поведение.Моделью может являться материальный объект, совокупность особым образом упорядоченных данных, система математических уравнений или компьютерная программа.Под моделированием понимают представление основных характеристик объекта исследования с помощью другой системы (материального объекта, совокупности уравнений, компьютерной программы). Перечислим принципы моделирования: 1. Принцип адекватности: Модель должна учитывать наиболее существенные стороны исследуемого объекта и отражать его свойства с приемлемой точностью. Только в этом случае результаты моделирования можно распространить на объект исследования. 2. Принцип простоты и экономичности: Модель должна быть достаточно простой для того чтобы ее использование было эффективно и экономически выгодно. Она не должна быть более сложной, чем это требуется для исследователя. 3. Принцип информационной достаточности: При полном отсутствии информации об объекте построить модель невозможно. При наличии полной информации моделирование лишено смысла. Существует уровень информационной достаточности, при достижении которого может быть построена модель системы. 4. Принцип осуществимости: Создаваемая модель должна обеспечивать достижение поставленной цели исследования за конечное время. 5. Принцип множественности и единства моделей: Любая конкретная модель отражает лишь некоторые стороны реальной системы. Для полного исследования необходимо построить ряд моделей, отражающих наиболее существенные стороны исследуемого процесса и имеющих что–то общее. Каждая последующая модель должна дополнять и уточнять предыдущую. 6. Принцип системности. Исследуемая система представима в виде совокупности взаимодействующих друг с другом подсистем, которые моделируются стандартными математическими методами. При этом свойства системы не являются суммой свойств ее элементов. 7. Принцип параметризации. Некоторые подсистемы моделируемой системы могут быть охарактеризованы единственным параметром (вектором, матрицей, графиком, формулой). Модель должна удовлетворять следующим требованиям: 1) быть адекватной, то есть отражать наиболее существенные стороны исследуемого объекта с требуемой точностью; 2) способствовать решению определенного класса задач; 3) быть простой и понятной, основываться на минимальном количестве предположений и допущений; 4) позволять модифицировать и дополнять себя, переходить к другим данным; 5) быть удобной в использовании. Связь компьютерного моделирования с другими методами познания показана из рис. 4. Объект познания исследуется эмпирическими методами (наблюдение, эксперимент), установленные факты являются основой для построения математической модели. Получившаяся система математических уравнений может исследоваться аналитическими методами или с помощью ЭВМ, –– в этом случае речь идет о создании компьютерной модели изучаемого явления. Проводится серия вычислительных экспериментов или компьютерных имитаций, и получающиеся результаты сопоставляются с результатами аналитического исследования математической модели и экспериментальными данными. Выводы учитываются для улучшения методики экспериментального изучения объекта исследования, развития математической модели и совершенствования компьютерной модели. Исследование социальных и экономических процессов отличается лишь невозможностью в полной мере использовать экспериментальные методы. 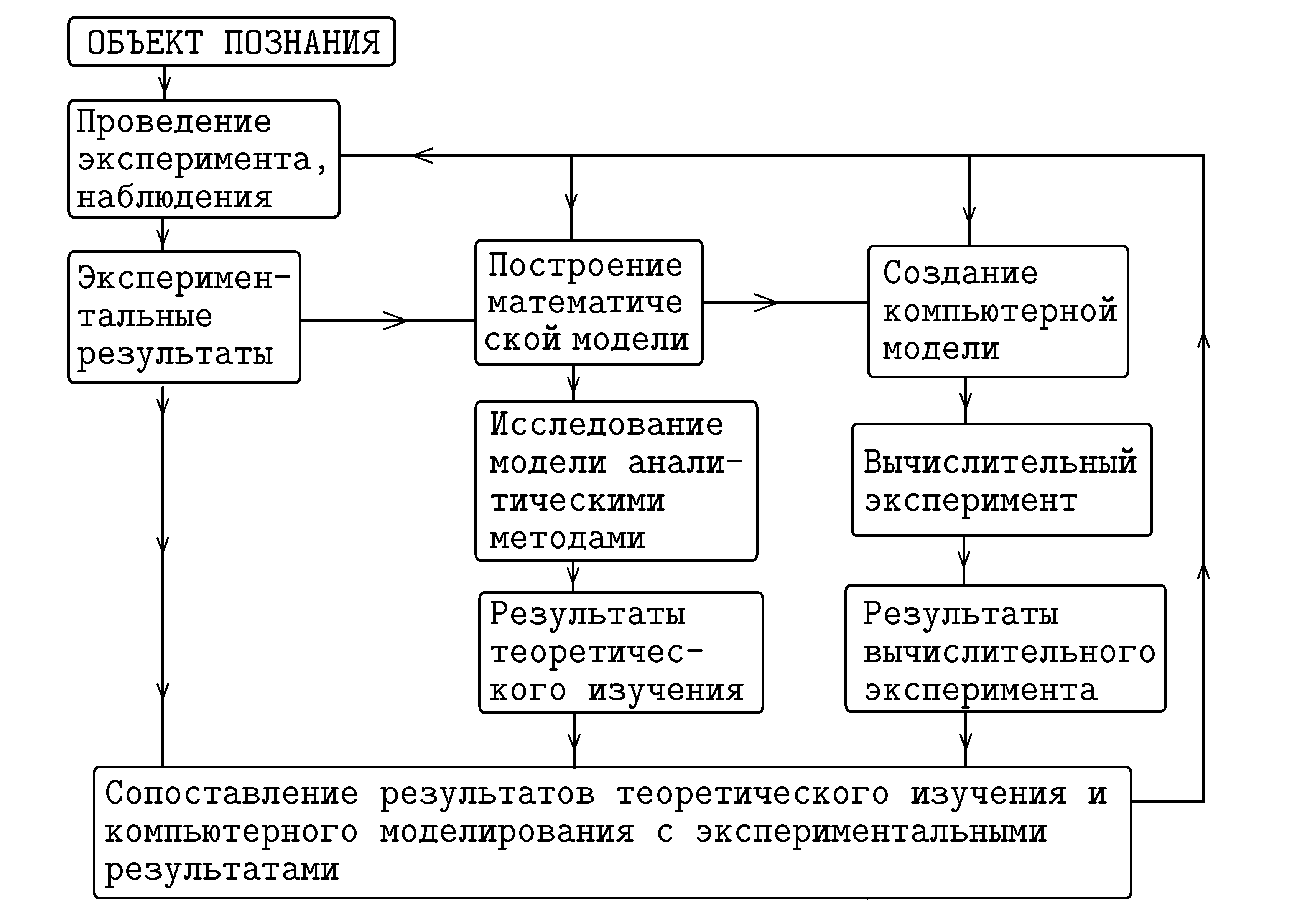 Рис. 4. Компьютерное моделирование среди других методов познания. |