Лаораторная 1. 1. моделирование как метод исследования содержание, цели и задачи учебной дисциплины Предметная область дисциплины
 Скачать 0.9 Mb. Скачать 0.9 Mb.
|
|
1.4. Роль и место моделирования и вычислительного эксперимента в исследовательской деятельности Вычислительный эксперимент. Этапы вычислительного эксперимента. Математическое и программное обеспечение эксперимента. Цикличность Вычислительный эксперимент Увеличив в сотни миллионов раз скорость выполнения арифметических и логических операций и повысив тем самым производительность интеллектуального труда человека, ЭВМ вызвали коренные изменения в области переработки информации. По существу, это явилось своего рода «информационной революцией». Первые крупные научные задачи, для решения которых успешно использовались ЭВМ, а точнее, для решения которых они и создавались, были связаны с овладением ядерной энергией и освоением космического пространства. В дальнейшем, развиваясь и совершенствуясь при решении разнообразных актуальных задач, этот стиль теоретического анализа трансформировался в новую современную технологию и методологию проведения теоретических исследований, которая получила название вычислительного эксперимента. Основой вычислительного эксперимента является математическое моделирование, теоретической базой – прикладная математика, а технической – мощные электронные вычислительные машины. Использование вычислительного эксперимента как средства решения сложных прикладных проблем имеет в случае каждой конкретной задачи и каждого конкретного научного коллектива свои специфические особенности. Тем не менее, всегда четко просматриваются общие характерные основные черты, позволяющие говорить о единой структуре этого процесса. В настоящее время технологический цикл вычислительного эксперимента принято подразделять на ряд этапов. И хотя такое деление условно, тем не менее, оно позволяет лучше понять существо этого метода. Во-первых, для исследуемого объекта строится модель. Сначала физическая, фиксирующая разделение всех действующих в рассматриваемом явлении факторов на главные, которые учитываются, и второстепенные, которые на данном этапе исследования отбрасываются. Одновременно формулируются допущения, или рамки применимости модели, в которых будут справедливы полученные на ее основе результаты. Эта модель записывается в математических терминах, как правило, в виде дифференциальных, интегральных или смешанных уравнений. Работа по конструированию математической модели чаще всего проводится объединенными усилиями физиков (химиков, биологов, медиков, экономистов), т.е. специалистов, хорошо знающих данную предметную область, и математиков, представляющих себе уровень развития соответствующего раздела прикладной математики и способных оценить возможность решения возникающей математической задачи. Вычислительный эксперимент не отвергает традиционных классических методов анализа, скорее напротив, предполагает их самое активное использование. Кроме того, на долю математиков выпадает и предварительное исследование математической модели – корректно ли поставлена задача, имеет ли она решение, единственно ли оно и т.д. Однако, для актуальных сложных задач, которые представляет современная наука и техника, подобное исследование удается выполнить лишь в исключительных случаях. Поэтому к решению задач, имеющих прикладной характер, зачастую приступают, не имея детального исследования ее математических свойств или изучив их лишь на частных упрощенных вариантах исходной постановки задачи. Второй этап вычислительного эксперимента связан с разработкой метода расчета сформулированной математической задачи, или, вычислительного алгоритма. Фактически он представляет собой совокупность цепочек алгебраических формул, по которым ведутся вычисления, и логических условий, позволяющих установить нужную последовательность применения этих формул. Как правило, для одной и той же математической задачи можно предложить большое число вычислительных алгоритмов. Однако из этого следует, что среди разнообразия алгоритмов не все одинаковы по своим качествам. Есть алгоритмы хорошие и плохие, и необходимо уметь отличать одни от других, не тратя времени и труда на программирование и расчеты. Для этого, нужно сформулировать критерии для оценки качества вычислительных алгоритмов. Эти вопросы и составляют предмет теории численных методов – раздела вычислительной математики, который стал особенно интенсивно развиваться с появлением ЭВМ. Общая цель этой теории – построение эффективных вычислительных методов, которые позволяют получить решение поставленной задачи с заданной точностью за минимальное количество действий (арифметических, логических), т.е. с минимальными затратами машинного времени. Вычислительный эксперимент имеет «многовариантный» характер, т.е. решение любой прикладной задачи зависит от многочисленных входных параметров. Получить решение соответствующей математической задачи в виде формулы, содержащей явную зависимость от параметров, для реальных задач, не удается. При использовании методов вычислительного эксперимента каждый конкретный расчет проводится при фиксированных значениях параметров. Проектируя оптимальную установку, т.е. определяя в «пространстве параметров» точку, соответствующую оптимальному режиму, приходится проводить большое число расчетов однотипных вариантов задачи, отличающихся значениями некоторых параметров. Поэтому необходимо, чтобы на один вариант задачи затрачивалось как можно меньше машинного времени. Третий этап вычислительного эксперимента – создание программы для реализации разработанного алгоритма на ЭВМ. В самом начале формулы алгоритма разбивались на отдельные операции: сложить, разделить, сравнить два числа по величине и т.д., и каждая операция программировалась отдельно. Поэтому развитие программирования шло по линии упрощения процесса общения человека с машиной, приближения форм этого общения к естественным. Так появились машинные языки, с помощью которых вести диалог с ЭВМ стало существенно легче. Каждый из языков был ориентирован на свой тип машин, на свой класс математических задач. Программное обеспечение (или математическое обеспечение) современной ЭВМ представляет собой сложную систему, включающую языки, трансляторы, операционные системы, библиотеки стандартных программ и пр. Это обеспечение составляет неотъемлемую часть ЭВМ, часто по стоимости превышающую стоимость собственно оборудования. Четвертый этап – собственно проведение расчетов на машине. На этом этапе проявляется сходство вычислительного эксперимента с реальным. Если в лаборатории экспериментатор с помощью специально построенной установки задает исследует реальную физическую модель, то специалисты по вычислительному эксперименту с помощью ЭВМ исследуют математическую. ЭВМ в процессе расчета может выдавать любую информацию, представляющую интерес для исследователя. Точность этой информации определяется достоверностью самой модели. По этой причине в серьезных прикладных исследованиях полномасштабным (или, как говорят, производственным) расчетам предшествуют тестовые расчеты. Они необходимы для того, чтобы «отладить» программу, т.е. отыскать и исправить все ошибки и опечатки, допущенные при создании алгоритма и его программной реализации. В предварительных расчетах тестируется также сама математическая модель, выясняется, насколько хорошо она описывает изучаемый класс явлений, ее адекватность реальности. Для этого проводится «обсчет» некоторых контрольных экспериментов, по которым имеются достаточно надежные измерения. Сопоставление этих данных с результатами расчетов позволяет уточнить математическую модель, повысить правильность предсказаний на ее основе. После проведения этой работы в вычислительном эксперименте наступают фаза прогноза – с помощью математического моделирования предсказывается поведение исследуемого объекта в условиях, где эксперименты пока не проводились или где они вообще невозможны. Пятый этап вычислительного эксперимента – обработка результатов расчетов, их всесторонний анализ и выводы. Эти выводы бывают в основном двух типов: проявляется необходимость уточнения модели или результаты, пройдя проверку на адекватность передаются заказчику. Однако чаще эти две стороны пересекаются – выясняются какие- либо необычные формы протекания изучаемого процесса, неожиданные режимы работы проектируемой установки. Математическая модель модифицируется (усложняется) и начинается новый цикл вычислительного эксперимента. Схематически циклы вычислительного эксперимента можно представить следующим образом: 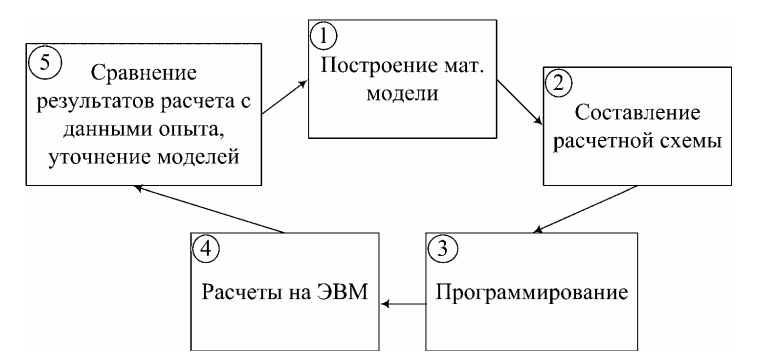 1.5. Классификация моделей: понятия математической и компьютерной модели, имитационное моделирование Под компьютерным моделированием в самом широком смысле будем понимать процесс создания и исследования моделей с помощью компьютера. Выделяют следующие виды моделирования: 1. Физическое моделирование: компьютер –– часть экспериментальной установки или тренажера, он воспринимает внешние сигналы, осуществляет соответствующие расчеты и выдает сигналы, управляющие различными манипуляторами. Например, учебная модель самолета, представляющая собой кабину, установленную на соответствующих манипуляторах, соединенных с компьютером, который реагирует на действия пилота и изменяет наклон кабины, показания приборов, вид из иллюминатора и т.д., имитируя полет реального самолета. 2. Динамическоеили численное моделирование, предполагающее численное решение системы алгебраических и дифференциальных уравнений методами вычислительной математики и проведение вычислительного эксперимента при различных параметрах системы, начальных условиях и внешних воздействиях. Используется для моделирования различных физических, биологических, социальных и других явлений: колебания маятника, распространение волны, изменение численности населения, популяции данного вида животных и т.д. 3. Имитационное моделирование состоит в создании компьютерной программы (или пакета программ), имитирующей поведение сложной технической, экономической или иной системы на ЭВМ с требуемой точностью. Имитационное моделирование предусматривает формальное описание логики функционирования исследуемой системы с течением времени, которое учитывает существенные взаимодействия ее компонентов и обеспечивает проведение статистических экспериментов. Объектно-ориентированные компьютерные симуляции используются для исследования поведения экономических, биологических, социальных и иных систем, для создания компьютерных игр, так называемого “виртуального мира”, обучающих программ и анимаций. Например, модель технологического процесса, аэродрома, некоторой отрасли производства и т.д. 4. Статистическое моделирование используется для изучения стохастических систем и состоит в многократном проведении испытаний с последующей статистической обработкой получающихся результатов. Подобные модели позволяют исследовать поведение всевозможных систем массового обслуживания, многопроцессорных систем, информационно-вычислительных сетей, различных динамических систем, на которые воздействуют случайные факторы. Статистические модели применяются при решении вероятностных задач, а также при обработке больших массивов данных (интерполяция, экстраполяция, регрессия, корреляция, расчет параметров распределения и т.д.). Они отличаются от детерминированных моделей,использование которых предполагает численное решение систем алгебраических или дифференциальных уравнений, либо замену изучаемого объекта детерминированным автоматом. 5. Информационное моделирование заключается в создании информационной модели, то есть совокупности специальным образом организованных данных (знаков, сигналов), отражающих наиболее существенные стороны исследуемого объекта. Различают наглядные, графические, анимационные, текстовые, табличные информационные модели. К ним относятся всевозможные схемы, графы, графики, таблицы, диаграммы, рисунки, анимации, выполненные на ЭВМ, в том числе цифровая карта звездного неба, компьютерная модель земной поверхности и т.д. 6. Моделирование знанийпредполагает построение системы искусственного интеллекта, в основе которой лежит база знаний некоторой предметной области (части реального мира). Базы знаний состоят из фактов (данных) и правил. Например, компьютерная программа, умеющая играть в шахматы (рис. 5), должна оперировать информацией о “способностях” различных шахматных фигур и “знать” правила игры. К данному виду моделей относят семантические сети, логических модели знаний, экспертные системы, логические игры и т.д. Логические модели используются для представления знаний в экспертных системах, для создания систем искусственного интеллекта, осуществления логического вывода, доказательства теорем, математических преобразований, построения роботов, использования естественного языка для общения с ЭВМ, создания эффекта виртуальной реальности в компьютерных играх и т.д. Исходя из целей моделирования, компьютерные модели подразделяют на группы: 1) дискриптивные модели, используемые для понимания природы исследуемого объекта, выявления наиболее существенных факторов, влияющих на его поведение; 2)оптимизационные модели, позволяющие выбрать оптимальный способ управления технической, социально-экономической или иной системой (например, космической станцией); 3) прогностические модели, помогающие прогнозировать состояние объекта в последующие моменты времени (модель земной атмосферы, позволяющая предсказать погоду); 4) учебные модели, применяемые для обучения, тренинга и тестирования учащихся, студентов, будущих специалистов; 5) игровые модели, позволяющие создать игровую ситуацию, имитирующую управление армией, государством, предприятием, человеком, самолетом и т.д., либо играющие в шахматы, шашки и другие логические игры. Области применения компьютерных моделей Совершенствование информационных технологий обусловило использование компьютеров практически во всех сферах деятельности человека. Развитие научных теорий предполагает выдвижение основных принципов, построение математической модели объекта познания, получение из нее следствий, которые могут быть сопоставлены с результатами эксперимента. Использование ЭВМ позволяет, исходя из математических уравнений, рассчитать поведение исследуемой системы в тех или иных условиях. Часто это единственный способ получения следствий из математической модели. Например, рассмотрим задачу о движении трех или более частиц, взаимодействующих друг с другом, которая актуальна при исследовании движении планет, астероидов и других небесных тел. В общем случае она сложна и не имеет аналитического решения, и лишь использование метода компьютерного моделирования позволяет рассчитать состояние системы в последующие моменты времени. Совершенствование вычислительной техники, появление ЭВМ, позволяющей быстро и достаточно точно осуществлять вычисления по заданной программе, ознаменовало качественный скачок на пути развития науки. На первый взгляд кажется, что изобретение вычислительных машин не может непосредственно влиять на процесс познания окружающего мира. Однако это не так: решение современных задач требует создания компьютерных моделей, проведения огромного количества вычислений, что стало возможным лишь после появления электронно–вычислительных машин, способных выполнять миллионы операций в секунду. Существенным является и то, что вычисления производятся автоматически, в соответствии с заданным алгоритмом и не требуют вмешательства человека. Если ЭВМ относится к технической базе проведения вычислительного эксперимента, то ее теоретическую основу составляют прикладная математика, численные методы решения систем уравнений. Успехи компьютерного моделирования тесно связаны с развитием численных методов, начавшегося с фундаментальных работ Исаака Ньютона, который еще в 17 веке предложил их использовать для приближенного решения алгебраических уравнений. Леонард Эйлер разработал метод решения обыкновенных дифференциальных уравнений. Из современных ученых весомый вклад в развитие компьютерного моделирования сделал академик А.А.Самарский, основоположник методологии вычислительного эксперимента в физике. Именно им была предложена знаменитая триада "модель – алгоритм – программа" и разработана технология компьютерного моделирования, успешно используемая для изучения физических явлений. В настоящее время вычислительный эксперимент используется для выполнения исследований в следующих направлениях: 1) расчет ядерных реакций; 2) решение задач небесной механики, астрономии и космонавтики; 3) изучение глобальных явлений на Земле, моделирование погоды, климата, исследование экологических проблем, глобального потепления, последствий ядерного конфликта и т.д.; 4) решение задач механики сплошных сред, в частности, гидродинамики; 5) компьютерное моделирование различных технологических процессов; 6) расчет химических реакций и биологических процессов, развитие химической и биологической технологии; 7) социологические исследования, в частности, моделирование выборов, голосования, распространение сведений, изменение общественного мнения, военных действий; 8) расчет и прогнозирование демографической ситуации в стране и мире; 9) имитационное моделирование работы различных технических, в частности, электронных устройств; 10) экономические исследования развития предприятия, отрасли, страны. |
