Алгоритмы - шпоры (Final). 1 Области рационального использования средств вт. Характеристики каждой из областей

• Название: 1 Области рационального использования средств вт. Характеристики каждой из областей
• Анкор: Алгоритмы - шпоры (Final).doc
• Дата: 14.05.2018
• Размер: 2.65 Mb.
• Имя файла: Алгоритмы - шпоры (Final).doc
• Тип: Документы; #19216
• страница: 5 из 6

55’ Способы определения параметра t в методе Ньютона по параметру.



.

Если функция не уменьшается, то шаг делится пополам.

На одном шаге:

– уменьшение шага. Многократные вычисления на одном шаге.






Если , то - метод Ньютона,

Если , то .

56’ Метод Ньютона с разделением переменных (блочная диагонализация матрицы Якоби). Сущность и область сходимости метода.

Применяется при незначительной разнице в фазах векторов напряжения в узлах, что соответствует нетяжелым режимам сети. Предполагается, что в виду малой зависимости P от U и Q от δ можно принять и .



Отсюда следует, что итерационный процесс описывается следующими уравнениями:



Решая последовательно эти системы уравнений относительно приращений δΔ и ΔU либо методом Гаусса, либо методом обращения матриц, можно получить значения независимых переменных на следующем шаге:




Его область сходимости небольшая – это нетяжелые режимы с небольшими разностями фаз напряжений в узлах.

57’ Модификации метода Ньютона, сокращающие объем вычислений на каждой итерации. Скорость и область сходимости этих методов.
К модификациям метода Ньютона, позволяющим сократить объем вычислений на каждом шаге относятся Модифицированный метод Ньютона и метод Ньютона с разделением переменных.
В модифицированном методе Ньютона сокращение числа расчетов достигается за счет устранения необходимости пересчета коэффициентов матрицы Якоби на каждом шаге итерационного процесса. Коэффициенты матрицы Якоби рассчитываются только один раз на первом шаге с нулевыми приближениями, и далее используется эта матрица. За счет подобного упрощения существенно страдает сходимость метода, так как значения коэффициентов матрицы Якоби могут достаточно существенно изменяться при переходе к следующему шагу.

В методе Ньютона с разделением переменных сокращение числа расчетов достигается за счет приравнивания нулю некоторых коэффициентов матрицы Якоби. Таким образом, расчеты выполняются быстрее, но это снова влияет на точность и скорость сходимости метода. В частности, из-за принимаемых допущений этот метод подходить только для расчета нетяжелых режимов сети.

58’ Методы расчета установившихся режимов сложных ЭЭС. Их сопоставление.
Абсолютно сходящихся методов нет!

Эффективность метода оценивается по 2 критериям:

1. 
   Количество вычислений на одной итерации;
   
2. 
   Общее число итераций для достижения заданной точности.
   

Методы – Зейделя (считает все, что считается), Ньютона + его модификации (сильно чувствительны к выбору начальных приближений) и градиентные методы.

Зейделя – см. 27, 28

Ньютона + модификации – см. 47, 52-54.

Градиентные – см. 67.

59’/60’ Использование метода Гаусса, обращения, L-H факторизации матрицы коэффициентов системы линейных алгебраических уравнений в расчетах режимов методом Ньютона.

При расчетах режимов методом Ньютона на каждом шаге приходится решать СЛАУ, например 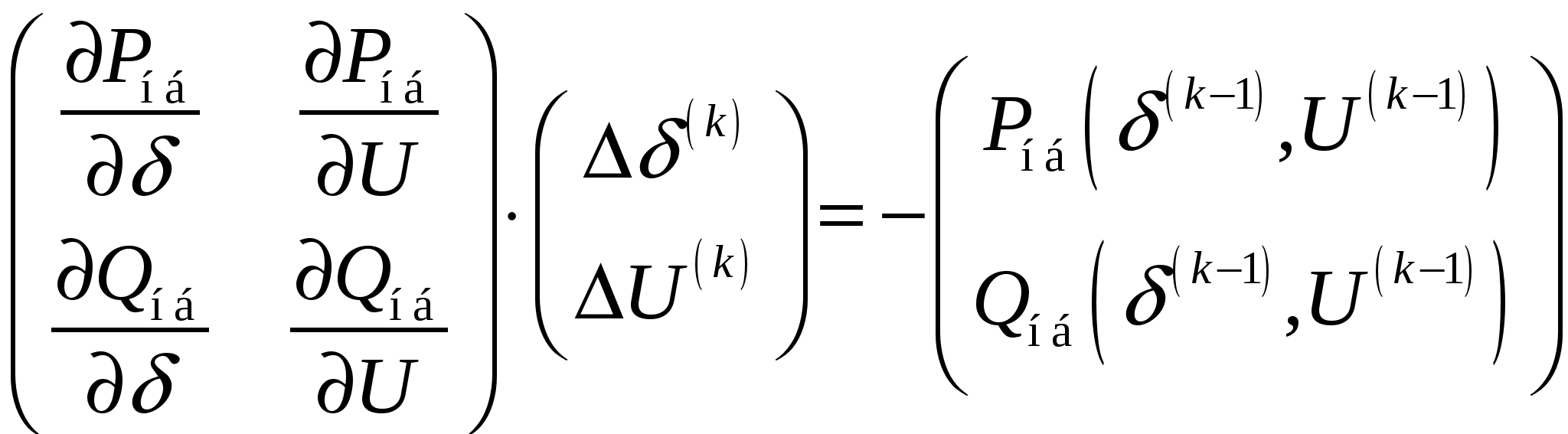. Причем метод ее решения может быть выбран из уже рассмотренных:

1. 
   Метод Гаусса – см. 18
   
2. 
   Обращения – суть метода сводится к получению обратной матрицы коэффициентов. Далее, путем ее домножения на столбец свободных членов, напрямую получается столбец неизвестных. Сложность метода состоит в сложности получения обратной матрицы.
   
3. 
   L-H факторизация – см. 35, 36.
   

61’ Характеристика современных программно-вычислительных комплексов (ПВК), содержащих расчет УР.
В настоящее время существуют программно-вычислительные комплексы, позволяющие значительно упростить расчет установившихся режимов энергосистем, и осуществлять ряд других смежных задач.
Основные из них:

А) РАСТР (расчет УР, эквивалентирование, расчет предельных режимов, оптимизация режимов по Q, РПН)

Б) ДАКАР (расчет УР с учетом изменения частоты, возможность учета СХН, потерь на корону, РПН, утяжеление режимов, расчет колебательной статической устойчивости, расчет эл.-мех. п.п., несимметричных и неполнофазных режимов, эквивалентирование)

В) МУСТАНГ (расчет УР с возможностью учета СХН и вставок постоянного тока, утяжеление режимов, расчет эл.-мех. п.п.)

Г) EUROSTAG (расчет УР с учетом изменения частоты, расчет колебательной устойчивости, динамической устойчивости, длительных п.п.)

Д) КОСМОС (расчеты УР по показаниям телеметрии, построение модели режима, утяжеление режима, оптимизация по Q, оптимизация по P для обеспечения функционирования энергорынка)