28’ Метод Зейделя применительно к решению нелинейного узлового ур-я в форме баланса токов.
YU=Uд-1S-YjбазUбаз примечание: над Uд-1S надо ^
Y11U1+
|
…..
|
+Y1nUn=
|
S1/U1-
|
Y1базUбаз
|
….
|
…..
|
|
|
|
Yn1U1+
|
…..
|
+YnnUn=
|
Sn/Un-
|
YnбазUбаз
|
Правая линейная часть, левая нелинейная часть.
U1(k)=1/Y11*( S1/U1(k-1)- Y1базUбаз-Y12U1 (k-1)- Y13U3 (k-1)-….. -Y1nUn (k-1))
U2(k)=1/Y22*( S2/U2(k-1)- Y2базUбаз-Y21U2 (k)- Y23U3 (k-1)-….. –Y2nUn (k-1))
………..
Un(k)=1/Ynn*( Sn/Un(k-1)- YnбазUбаз-Yn1U1 (k)- Yn2U2 (k)-….. –Yn-1nUn-1 (k))
Итерационная формула Зейделя:
Ui(k)=1/Yii*( Si/Ui(k-1)- YiбазUбаз-Σ(i-1) YijUj (k)-Σ YijUj (k-1))
Sбал=UбалΣYбалjUj
Должно быть задано макс. кол-во итераций, номер балансирующего узла,точность
max ׀Ui (k)- Ui (k-1)׀≤εk≈0.5÷0.05
max ׀Pнб׀≤εр ≈ 0.5 МВт max ׀Qнб׀≤εQ ≈ 1 Мвар
Примечание: везде над S/U надо поставить ^
Св-ва:
1) В алгоритмическом отношении очень прост(программир-ся только 1 ф-ла)
2) естественным образом учитывает слабую заполненность матрицы узловых проводимостей;
3) сход-ть мож быть оценена по достаточным условиям сх-ти СЛАУ
4) область сходимости не очень велика , т.е. при расчете тяжелых режимов, близких к пределу по существованию метод З расходится
5) нечувствителен к начальным приближениям
6) сходится достаточно медленно
Для ускорения используют коэффициент ускорения
|
29’ Алгоритмическая и программная реализация метода Зейделя. См. 28
Программа:
Subroutine zeidel (y,U, S, l,n, max, ib,eps)
Complex y(l,l), U(n), S(n), c
do iter=1,max
k=0
do i=1,n
if (i.ne.ib) then
coniq (S(i)/U(i))
do j=1,n
if (i.ne.j) c=c-y(i,j)*U(j)
end do
c=c/y(i,i)
if ( c abs(U(i)-c) . gt. eps) k=1
U(i)=c
end if
end do
it=iter
if (k.eq.0) exit
end do
if (k.eq.0) then
S(ib)=(0,0)
do i=1,n
S(ib)=S(ib) +y(ib, j)*U(j)
end do
S(ib)=conjq(S(ib))*U(ib)
write (3,1) it
1_format (5x, « кол-во итераций it=» , ib)
else
write (3, «(‘итерационный процесс не сходится’)»)
stop
end if
return end
|
30’ Свойсва метода Зейделя, используемого для расчета установившихся режимов сложных ЭЭС. Коэффициент ускорения.
Св-ва:
1) В алгоритмическом отношении очень прост(программир-ся только 1 ф-ла)
2) естественным образом учитывает слабую заполненность матрицы узловых проводимостей;
3) сход-ть мож быть оценена по достаточным условиям сх-ти СЛАУ , в частности их можно оценивать как условия сх-ти в методе простой итерации: i≠ j
׀Yii׀>Σ׀ ijY׀
а) если в схеме нет поперечных ветвей (емкостных проводимостей) и узел связан с базисным узлом, то достаточные условия сходимости выполняются
Yii= Σ ׀ -Yi-j-Yi-δ ׀ => ׀Yii׀>Σ׀ ijY-׀
б) если мы не имеем емкостных проводимостей на землю и узел не связан с базисным балансирующим узлом
׀Yii׀≤Σ׀ ijY׀, если есть трансформаторная ветка ׀Yii׀< Σ ׀ -Yi-j-Yт/кт ׀
в) если в схеме есть поперечная емкостная проводимость и узел не связан с базисным Yii= Σ ׀ -Gi-j +jBi-j -jBi-0 ׀ => ׀Yii׀<Σ׀ ijY׀
достаточное условие не выполняется; Если дост условия выполняются, то сходится. Если нет – то либо сх либо не сходится
4) область сходимости не очень велика , т.е. при расчете тяжелых режимов, близких к пределу по существованию метод З расходится
5) нечувствителен к начальным приближениям
6) сходится достаточно медленно
Для ускорения используют коэффициент ускорения
Uiq (k)= Uiq (k-1)+q(Ui (k)- Uiq (k-1)) Пример: n=75, 220/110, nг=11
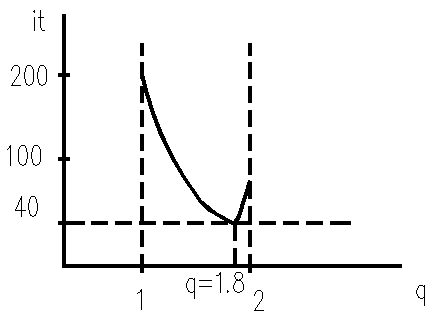
|
31’ Достаточное условие сходимости метода Зейделя применительно к решению нелинейного узлового уравнения в форме баланса токов.
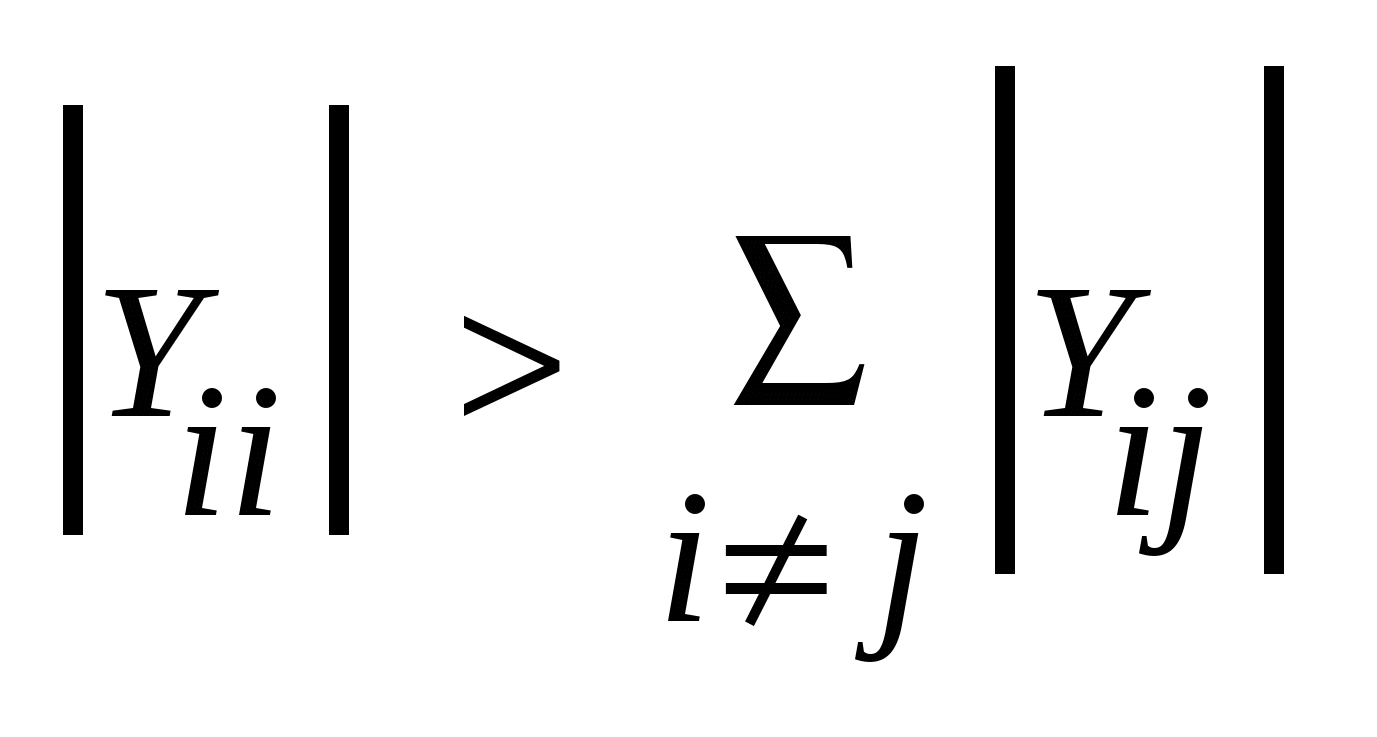
а) Если в схеме нет поперечных ветвей (емк. проводимостей на землю) и узел связан с базисным узлом, то достаточные условия сходимости выполняются.
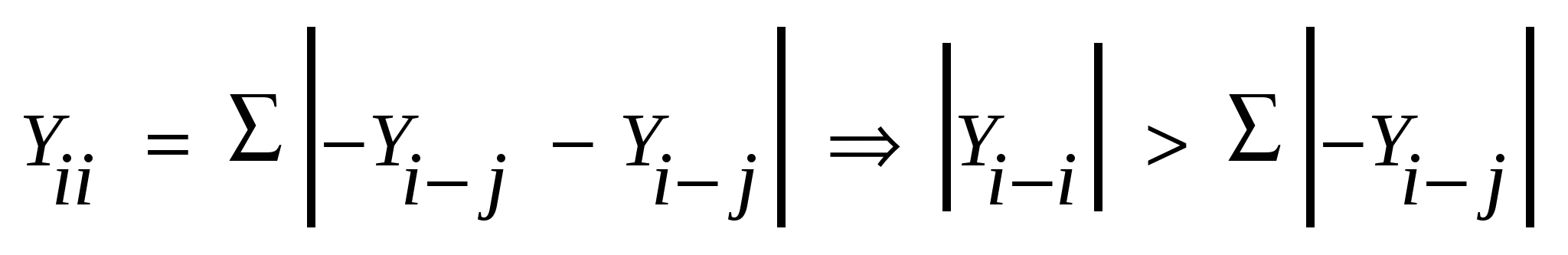
б) Если нет емкостных проводимостей на землю и узел не связан с базисным балансирующим узлом
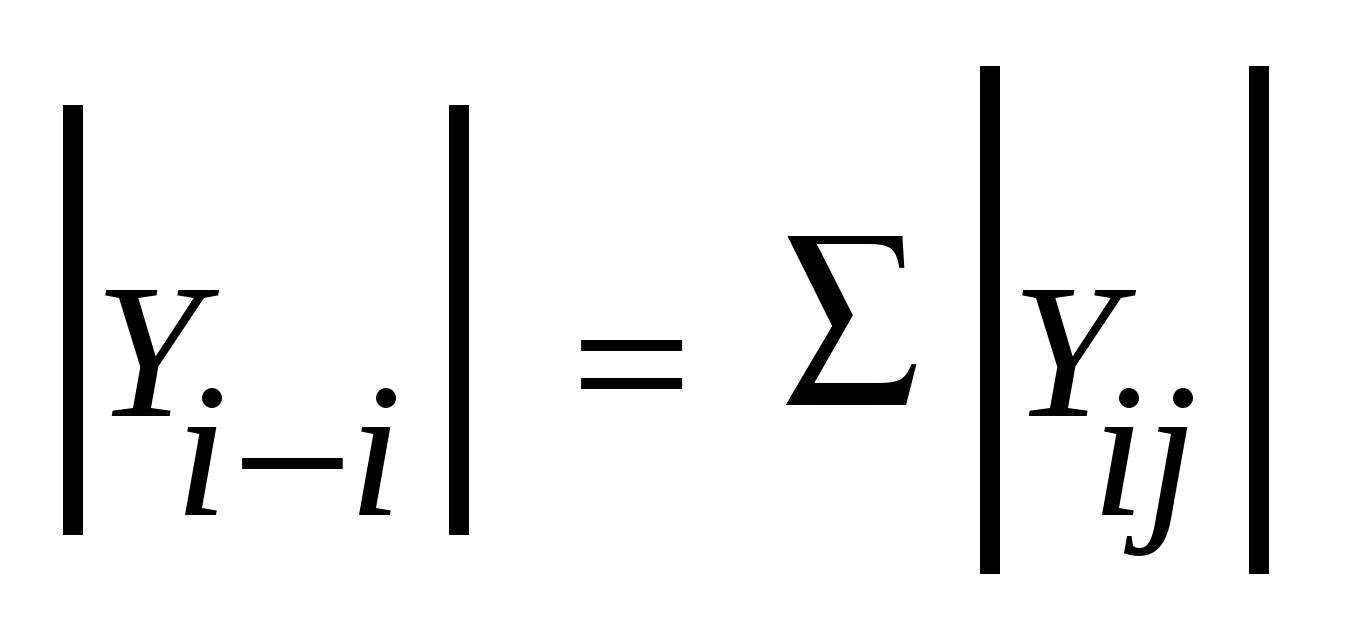
Если есть трансформаторная ветка
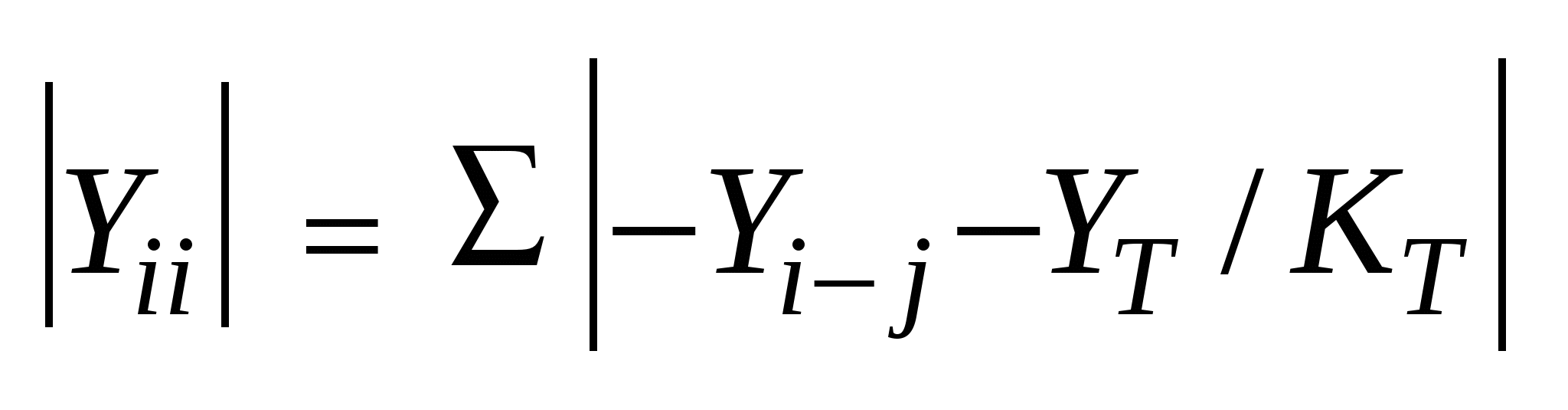
в) Если в схеме имеется поперечная емкостная проводимость и узел не связан с базисным узлом.
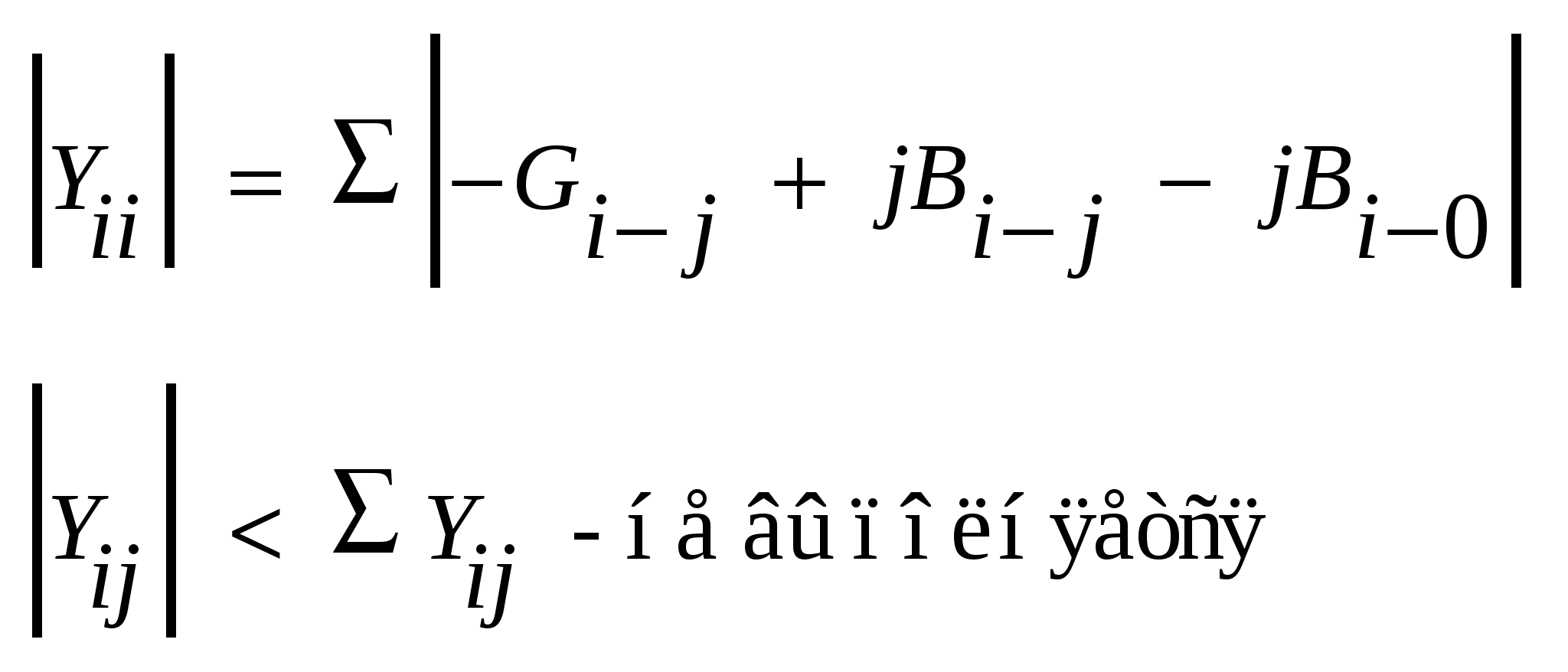 , следовательно , следовательно
Метод Зейделя не сойдется, если в ветви есть явновыраженный УПК
Если достаточные условия выполняются, то сходится. Если нет – то либо сх либо не сходится.
|
32’ Вычислительная схема метода Зейделя при задании ген. узлов в форме Pг, Uг
ген. Узел задан опорным, нам нужно найти Q
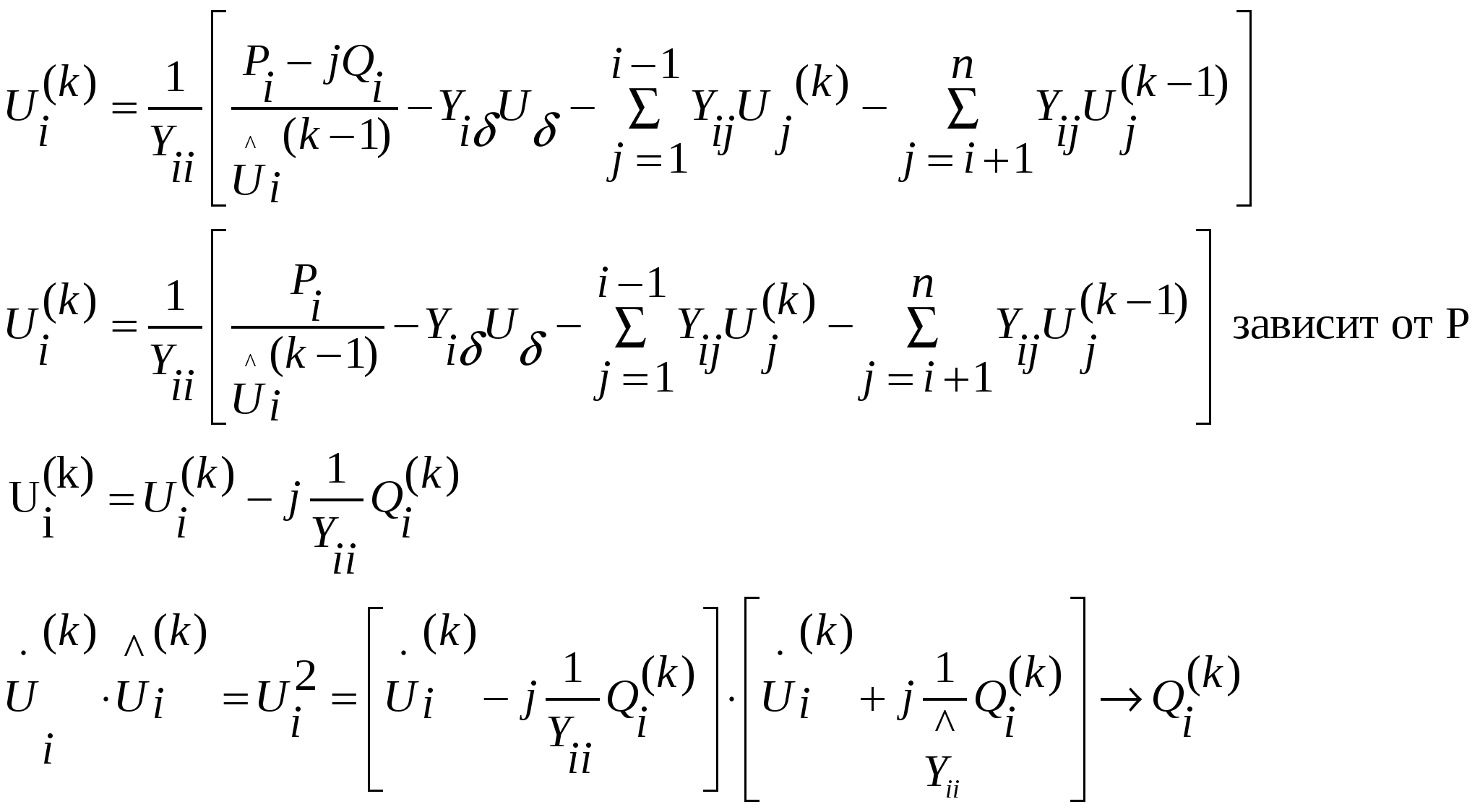
|
33’ Решение уравнения в форме баланса токов на основе метода Гаусса. Блок-схема алгоритма установившегося режима.
Правая нелинейная часть принимается линейной.
Если режим находится далеко от предела по устойчивости, то кол-во итераций при решении линейной и нелинейной системы уравнений одинаково (и сходимость). Сходимость определяется св-вами матрицы Y.
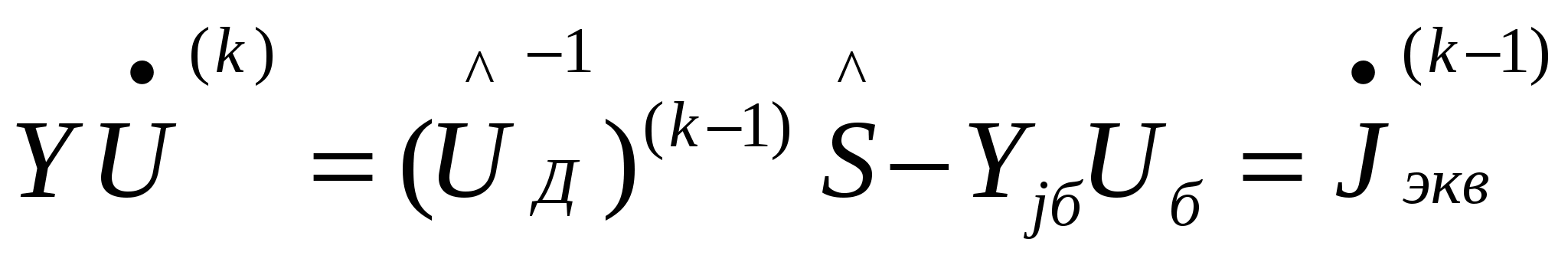 - вычисляем - вычисляем
На каждой внешней итерации - метод Гаусса.
На каждой внутр итерации – решаем алгебр систему линейных уравнений методом гаусса
|
34’ Решение нелинейного узлового уравнения в форме баланса токов на основе обращения матрицы Y. Блок-схема алгоритма-расчёта установившегося режима.
Нелинейное уравнение в форме баланса токов: 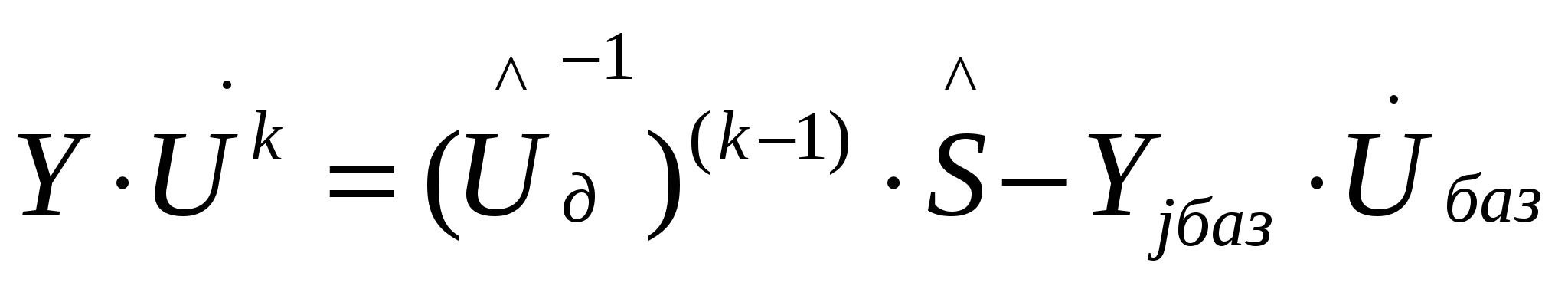
Обращение: 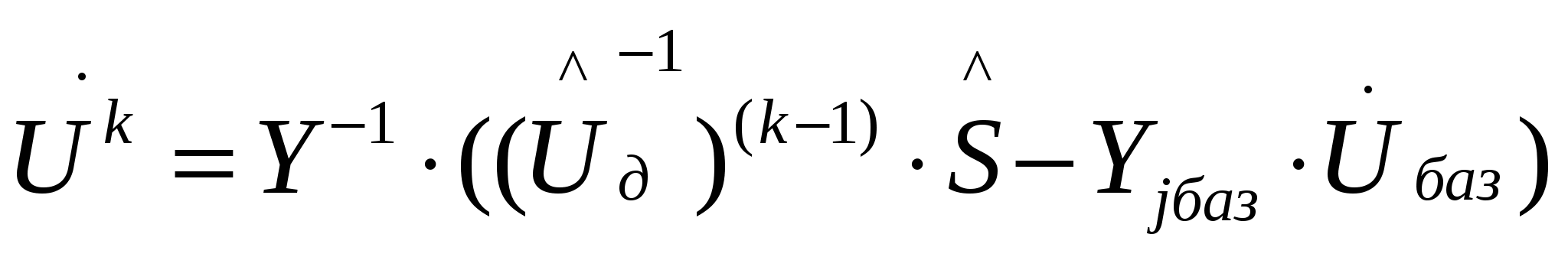
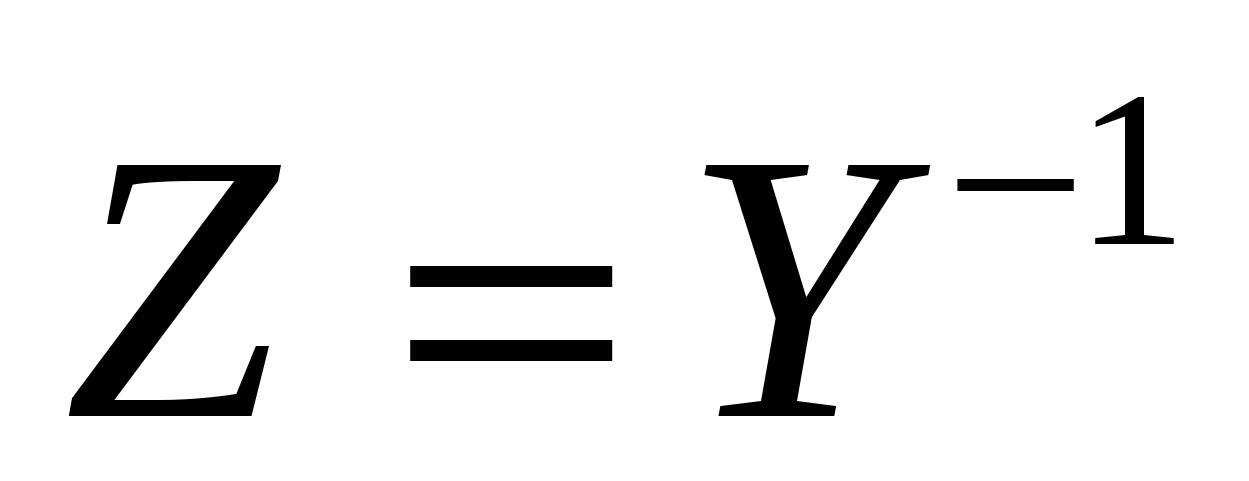 -вычисляется один раз (это +). Первоначально слабозаполненная Y превращ в полностью заполненную матрицу Z (это -) -вычисляется один раз (это +). Первоначально слабозаполненная Y превращ в полностью заполненную матрицу Z (это -)
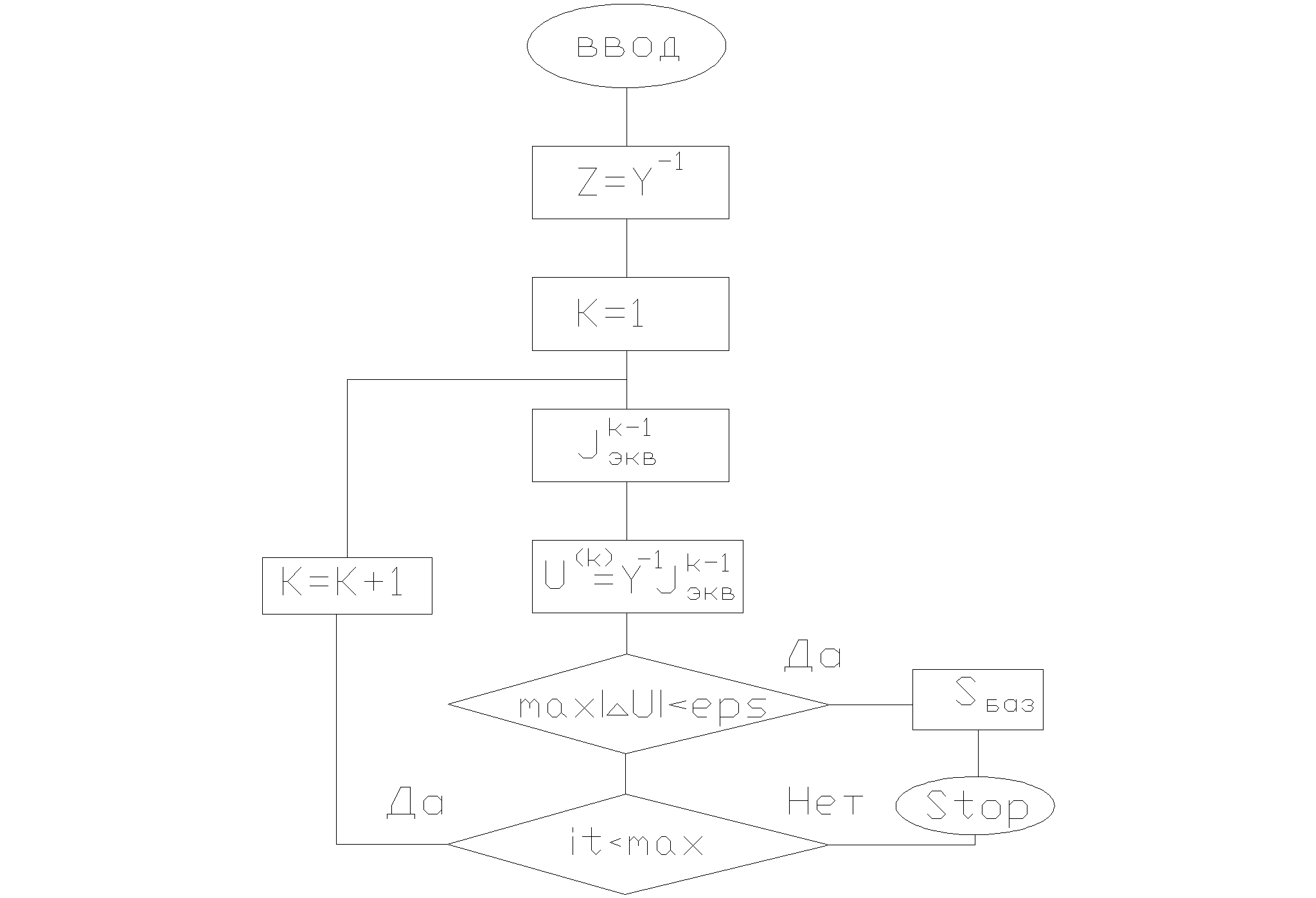
Первоначально заполненная матрица Y превратилась в полностью заполненную Z.
|
35’ Решение нелинейного узлового уравнения в форме баланса токов на основе L-H факторизации матрицы Y. Блок-схема алгоритма расчета установившегося режима.
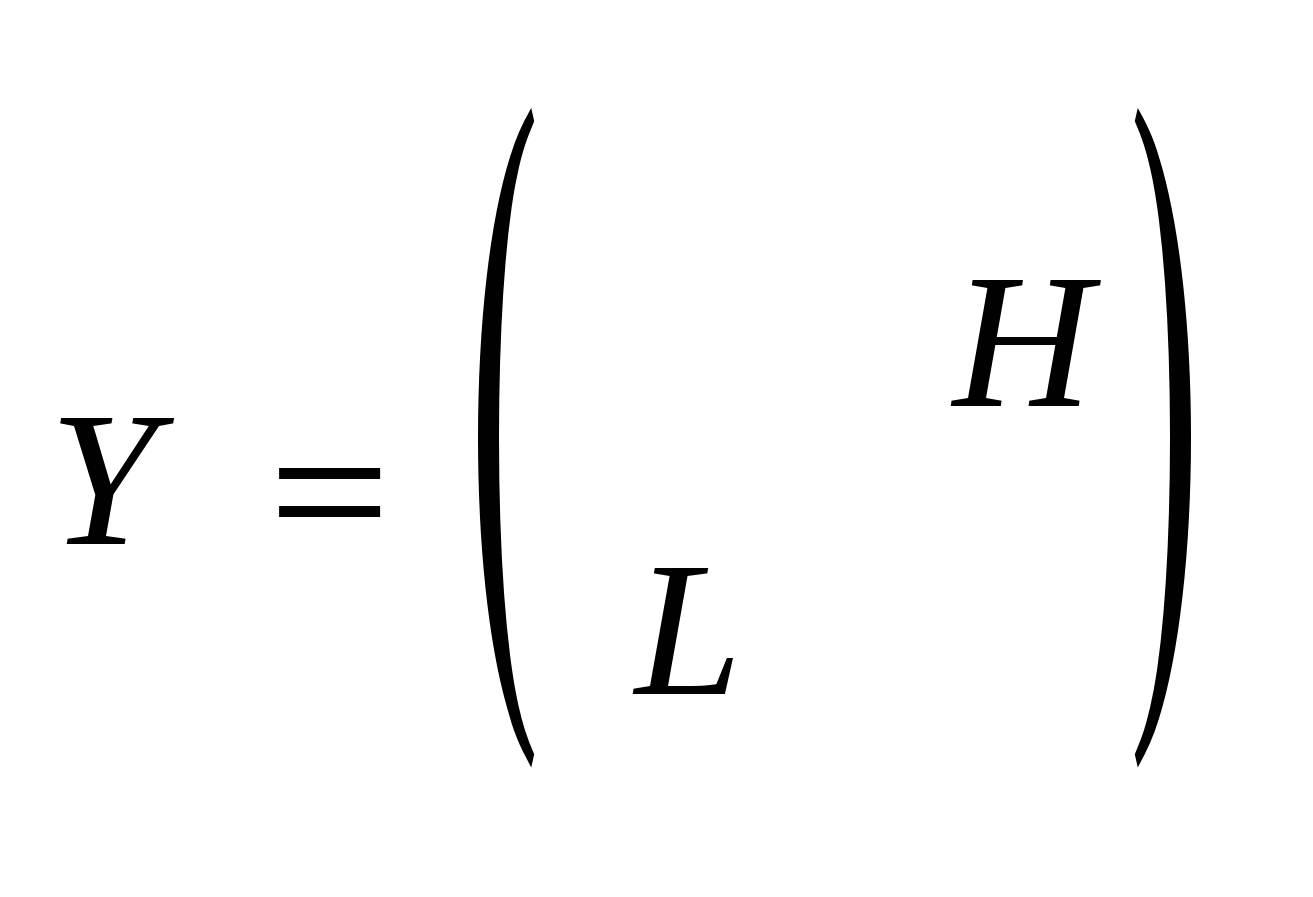
|
Нелинейное уравнение в форме баланса токов:
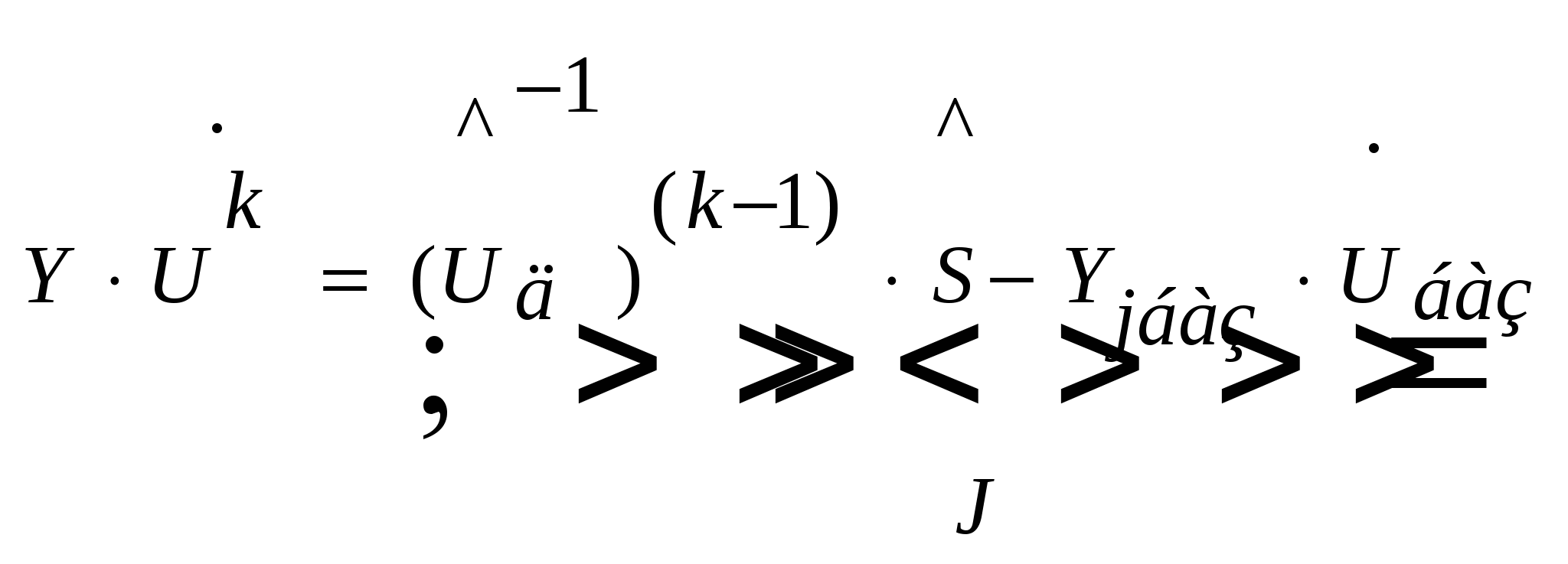
|
Совмещает достоинства методов обращения и Гаусса:
1)Операция факторизации только 1 раз → слабозаполнен. Матрицы L и H. 2)Вычисления существенно проще Гаусса, где на каждой итерации пересчит. матрица; алгоритмич прост.
“-“ ген. узлы только неопорные
Вывод: ↓ объем вычислений и объем требуемой памяти.
|
 Скачать 2.65 Mb.
Скачать 2.65 Mb.