Навигация по странице:37’ L-H факторизация матрицы коэффициентов системы линейных алгебраических уравнений (матрицы А). Алгоритм вычисления элементов факторизованной матрицы.38’ Алгоритмическая и программная реализация L-H факторизации матрицы А.39’/41’ Методы, используемые для расчета УР при записи узловых уравнений в форме баланса токов. / Методы, применяемые для решения комплексного узлового уравнения в форме баланса токов.40’ Методы расчета режимов, основанные на сочетании методов Зейделя и Гаусса. Достоинства и недостатки.42’ Методы расчета установившегося режима, требующие разделения узлового уравнения в комплексной форме на два уравнения с действительными коэффициентами. Прямоугольная и полярная системы координат.43’ Узловое уравнение в форме баланса мощности, записанное в прямоугольной системе координат.45’ Узловое уравнение состояния эл. сист. в форме баланса мощности, записанное в полярной системе координат.46’ Возможные формы записи нелинейных узловых уравнений установившегося режима для решения их методами, требующими разделения комплексных переменных на действит.сост.47’ Метод Ньютона. Решение узлового уравнения методом Ньютона, записанного в прямоугольной и полярной системе координат.48’/49’ 3ависимость размерности матрицы Якоби от формы представления генераторных узлов и системы координат, в которой записаны узловые уравнения в форме баланса мощности.50’ Аналитическое выражение элементов матрицы Якоби узловых уравнений в форме баланса мощности, записанных в полярной системе координат.51’ Свойства матрицы Якоби. Свойства метода Ньютона. Св-ва матрицы Якоби53’ Модифицированный метод Ньютона. Сущность и область сходимости.54’ Метод Ньютона по параметру. Сущность и область метода.
|
Алгоритмы - шпоры (Final). 1 Области рационального использования средств вт. Характеристики каждой из областей
З6’ Решение уравнений установившегося режима на основе L-H факторизации матрицы коэффициентов. Вычислительная схема прямой и обратной подстановки.
1-й этап: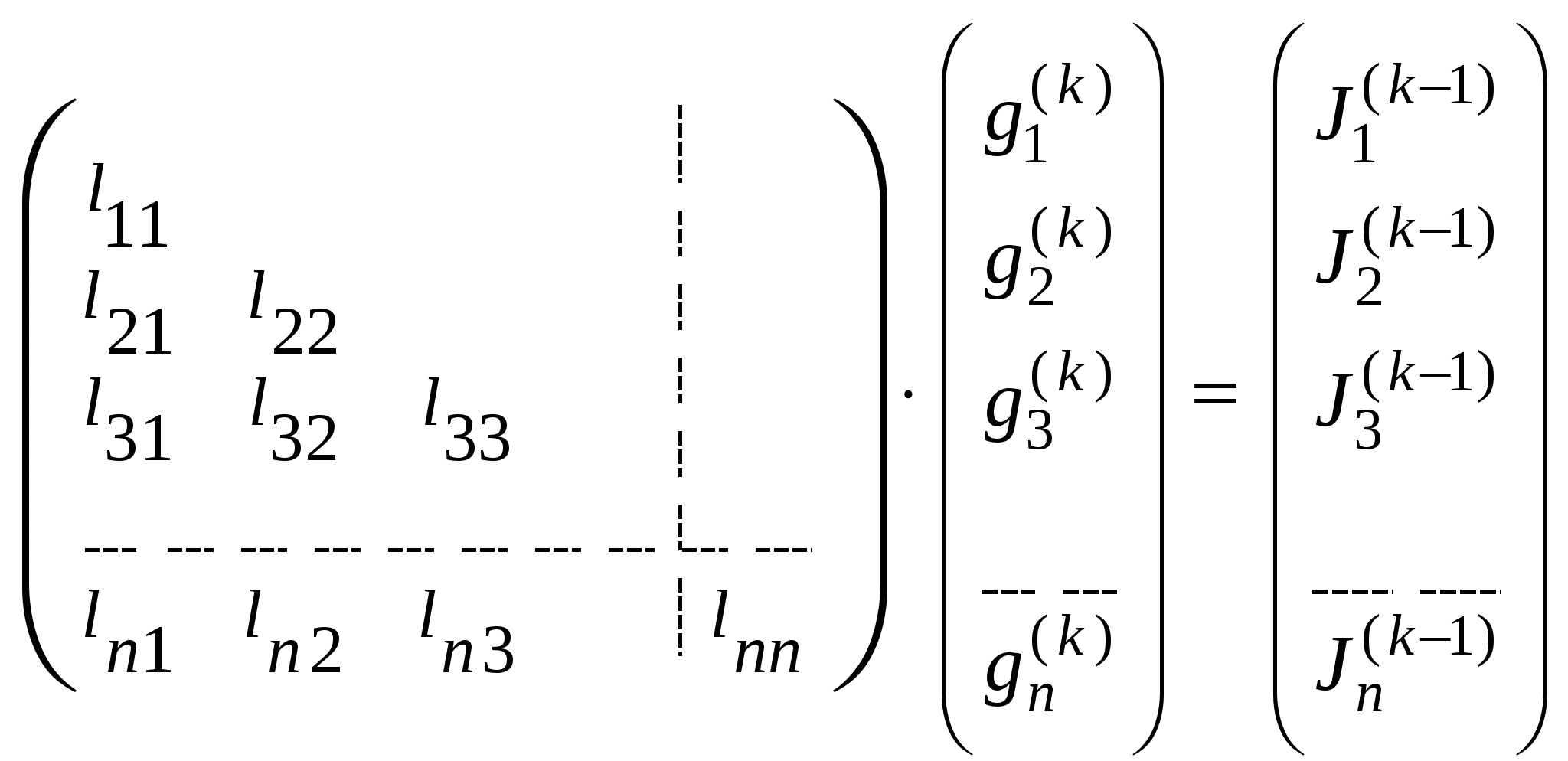 
Решается прямой подстановкой
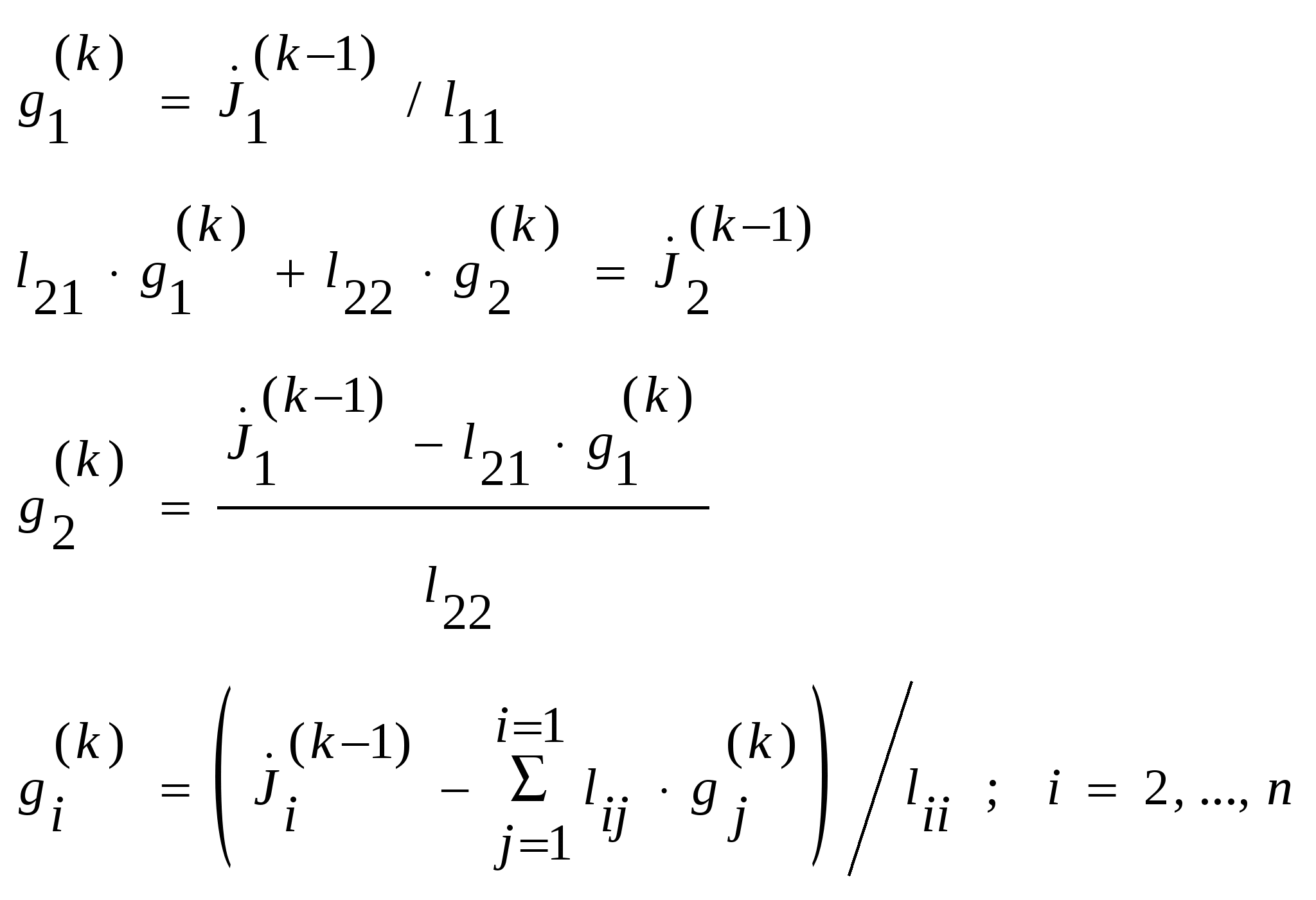
2-й этап: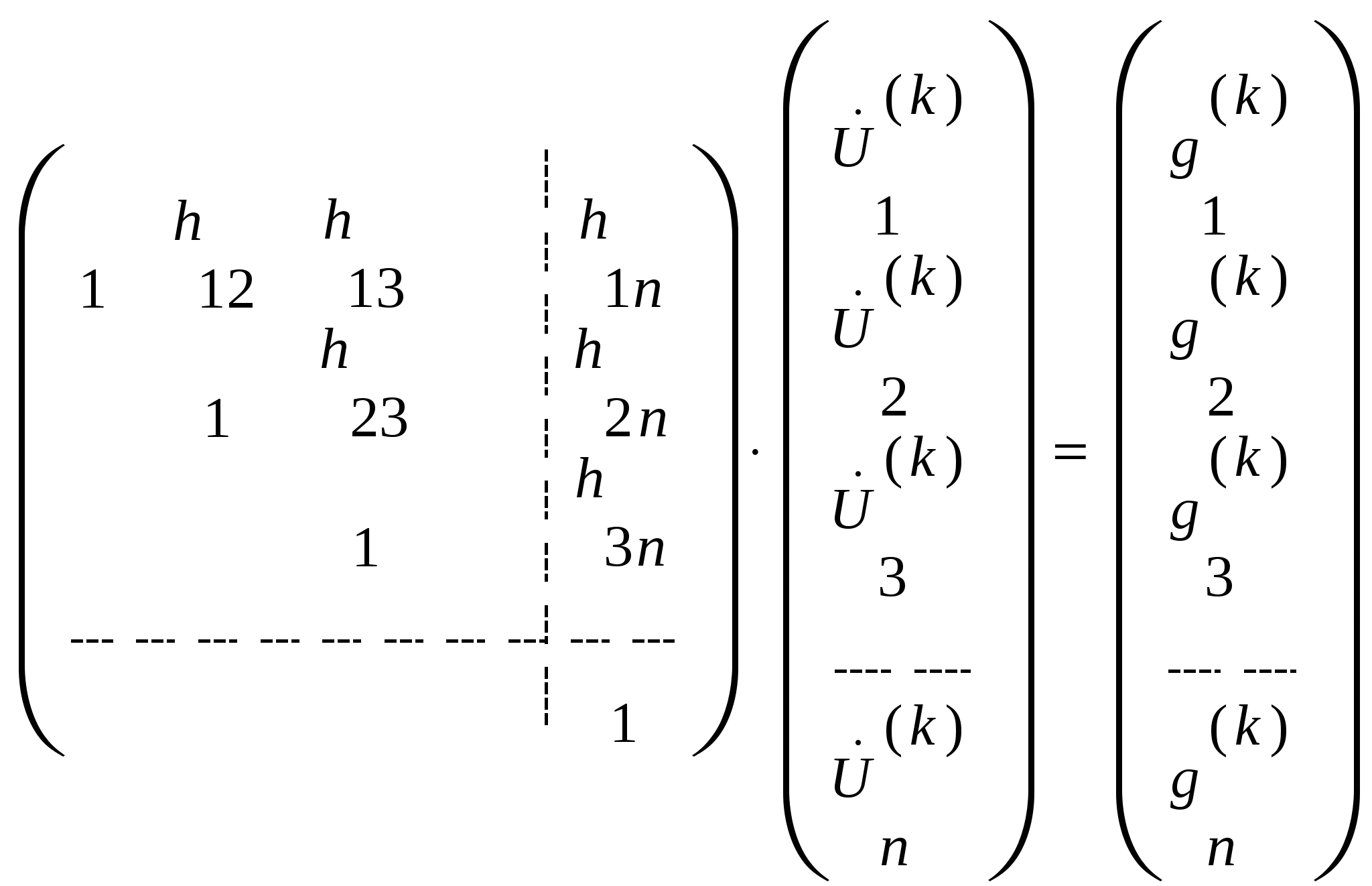 
Решается обратной подстановкой
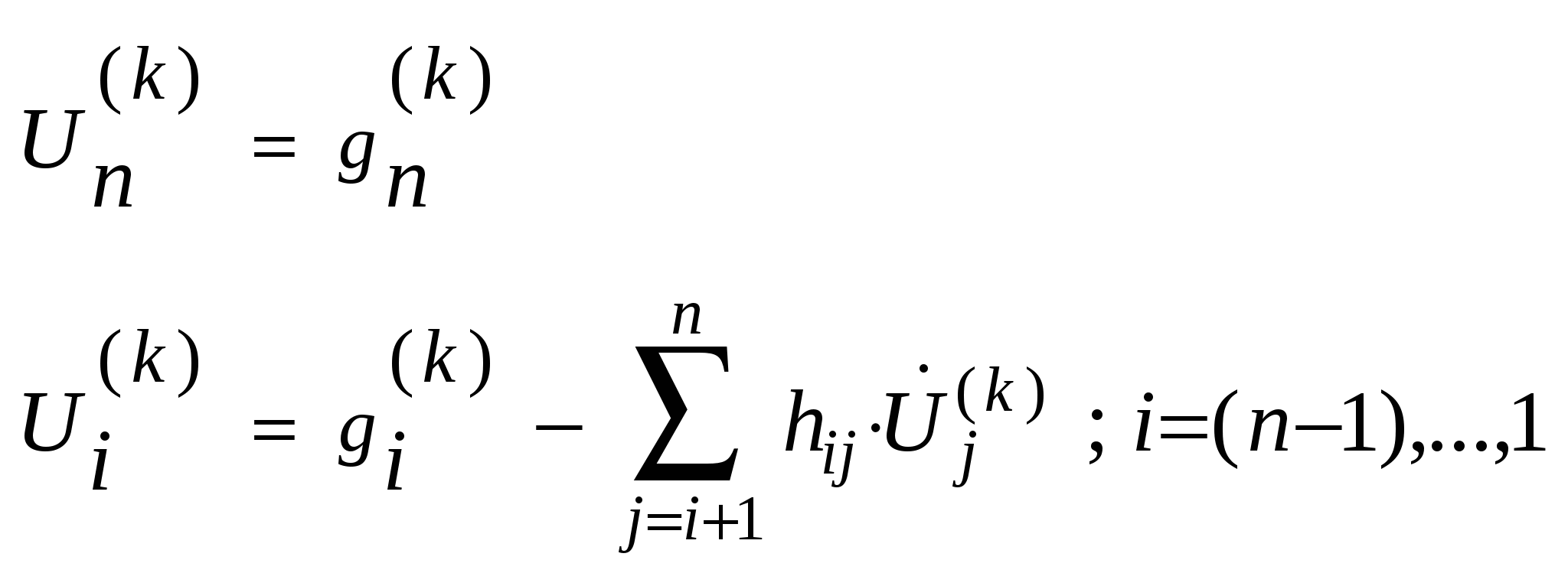 только везде вместо g -> q
|
37’ L-H факторизация матрицы коэффициентов системы линейных алгебраических уравнений (матрицы А). Алгоритм вычисления элементов факторизованной матрицы.
|
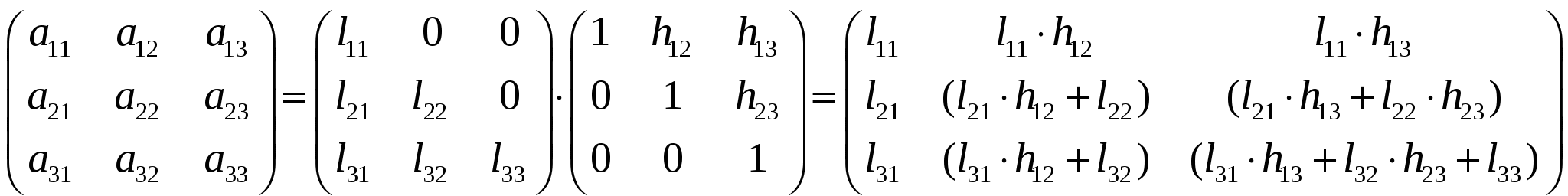
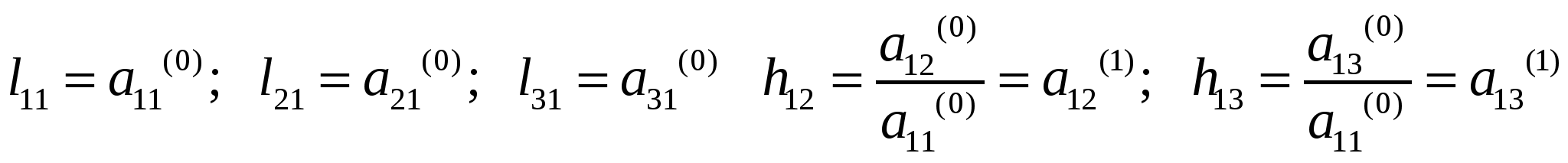
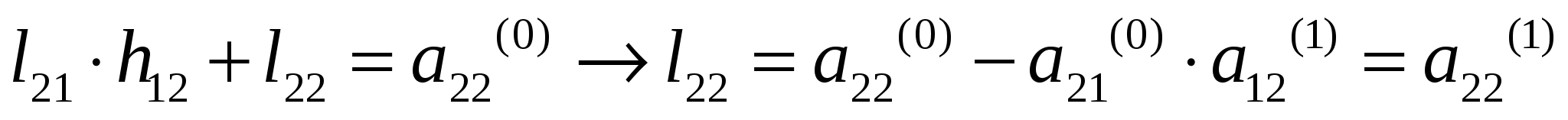
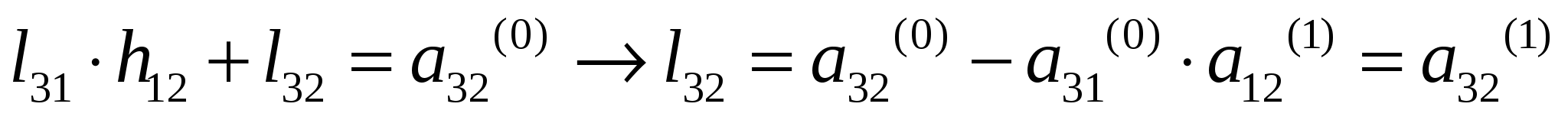
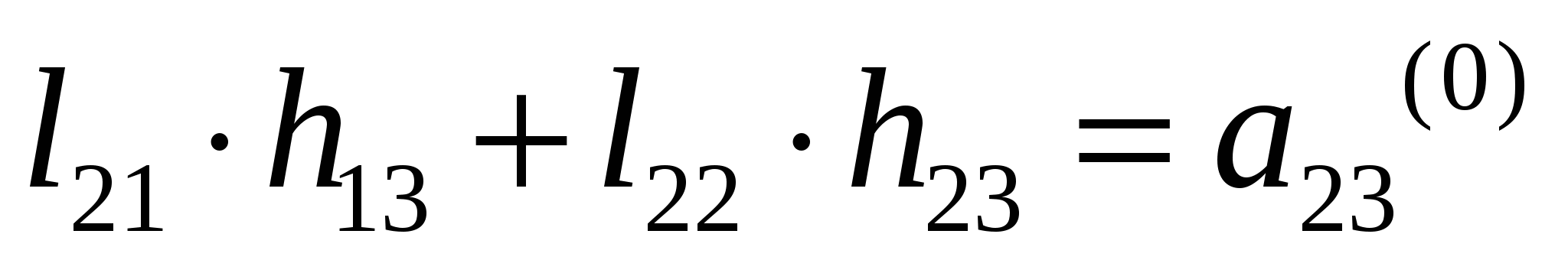
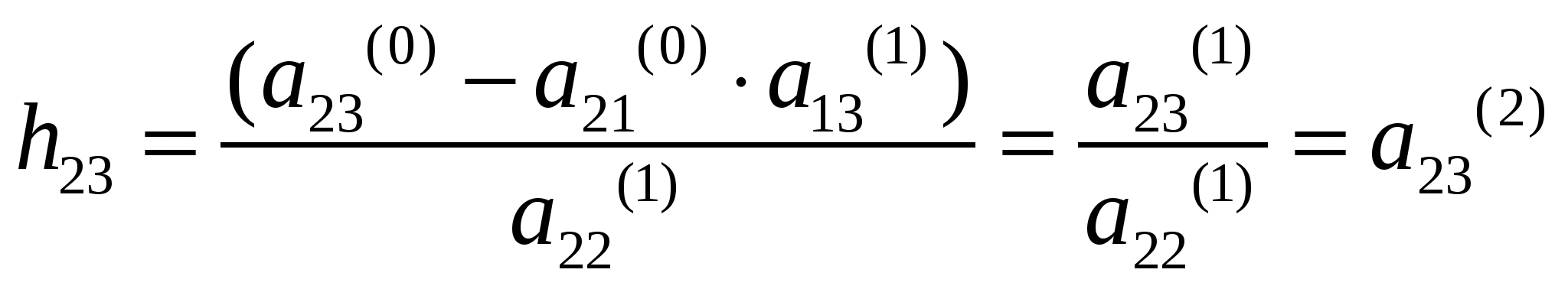
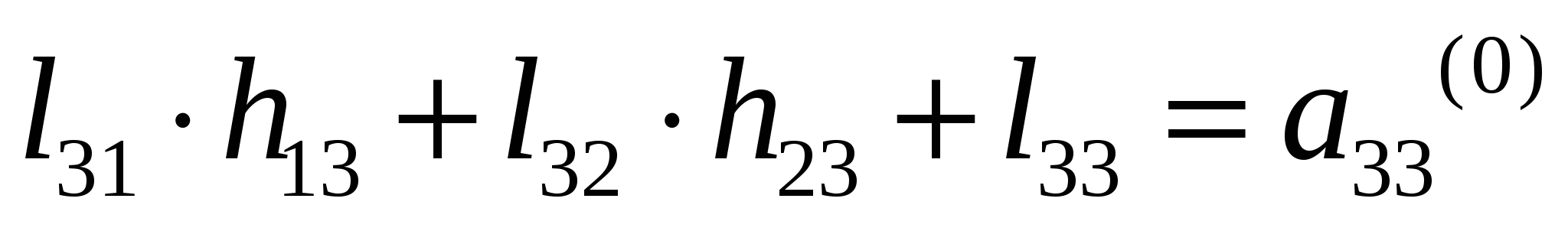
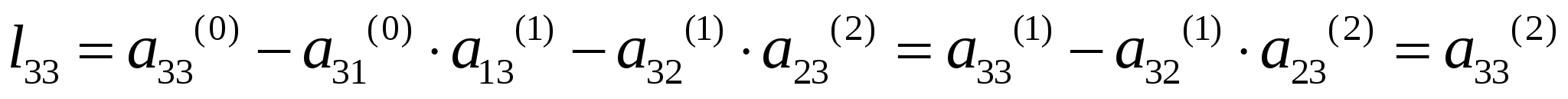
38’ Алгоритмическая и программная реализация L-H факторизации матрицы А.
Subroutine lhfact (A,n,l)
Complex A(l,l),t
Do k=1, n-1
Do j=k+1, n
t=a(k,j)/a(k,k)
do i=k+1, n
a(i,j)=a(i,j)-a(i,k)*t
enddo
enddo
enddo
return
end
Совмещает достоинства методов обращения и Гаусса:
1)Операция факторизации только 1 раз → слабозаполнен. Матрицы L и H.
2)Вычисления существенно проще Гаусса, где на каждой итерации пересчит. матрица; алгоритмич прост.
“-“ ген. узлы только неопорные
Вывод: ↓ объем вычислений и объем требуемой памяти.
Алгоритм см билет 36!
|
39’/41’ Методы, используемые для расчета УР при записи узловых уравнений в форме баланса токов. / Методы, применяемые для решения комплексного узлового уравнения в форме баланса токов.
1) Метод Зейделя
- прост в алгоритмическом отношении
- естественным образом учитывает слабую заполненность матрицы узловых проводимостей
- при расчете утяжеленных режимов область сходимости невелика
- нечувствителен к начальным приближениям
2) Метод Гаусса
- важным достоинством является высокая скорость решения
- надо хранить в памяти как исходную, так и пересчитанную матрицы
- на каждом шаге прямого хода надо выбирать главный элемент
3) Метод обращения матрицы Y
- обращение матрицы узловых проводимостей проводится 1 раз
- из слабозаполненной матрицы Y получается сильнозаполненная Z
4) LH-факторизация
Совмещает достоинства методов обращения и Гаусса.
- операция факторизации производится 1 раз => слабозаполненные матрицы L и H
- вычисления существенно проще метода Гаусса, где на каждой итерации пересчитывается матрица; алгоритмически прост
- может использоваться только с НЕОПОРНЫМИ ген. узлами.
=> малый объем вычислений и памяти ПК.
|
40’ Методы расчета режимов, основанные на сочетании методов Зейделя и Гаусса. Достоинства и недостатки.
Матрицу Y разбиваем на блоки, выделяя блок генераторных и опорных узлов.
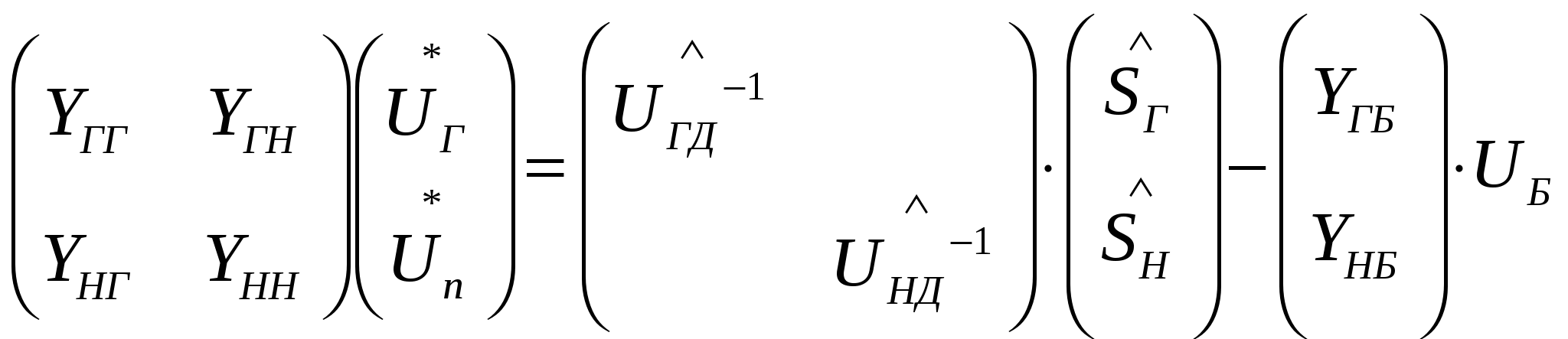
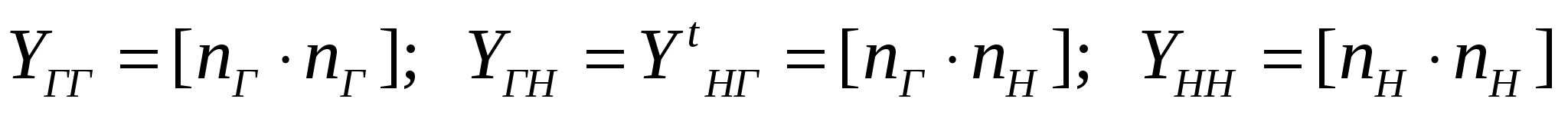
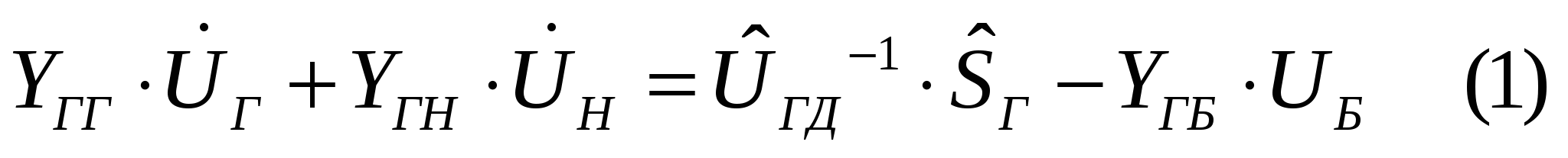
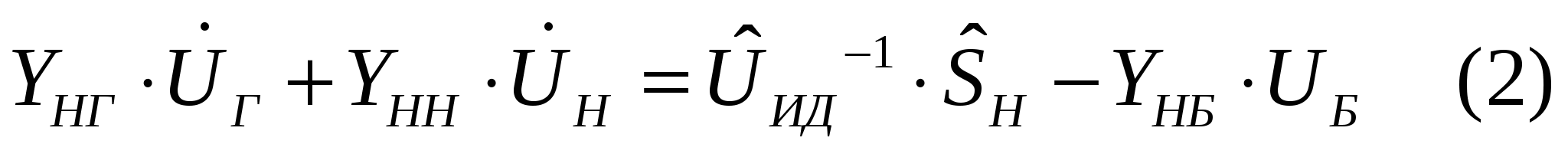
Решая ур-е (1) методом Зейделя относительно напряжений в ген. оп. Узлах, получим:
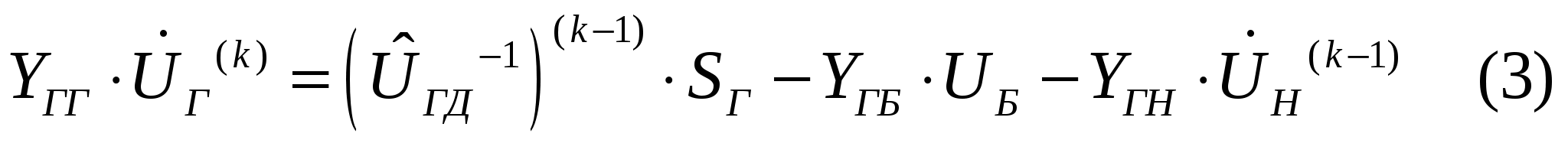
Из ур-я (3):
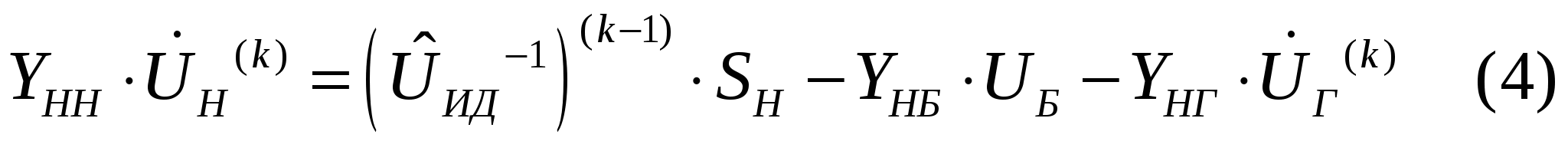
Ур-е (4) решаем на основе метода Гаусса, ищем комплексы напряжений в нагрузочных узлах.
Только метод Зейделя даст возможность учесть опорные ген. узлы.
|
42’ Методы расчета установившегося режима, требующие разделения узлового уравнения в комплексной форме на два уравнения с действительными коэффициентами. Прямоугольная и полярная системы координат.
Поскольку брать производные по комплексным величинам 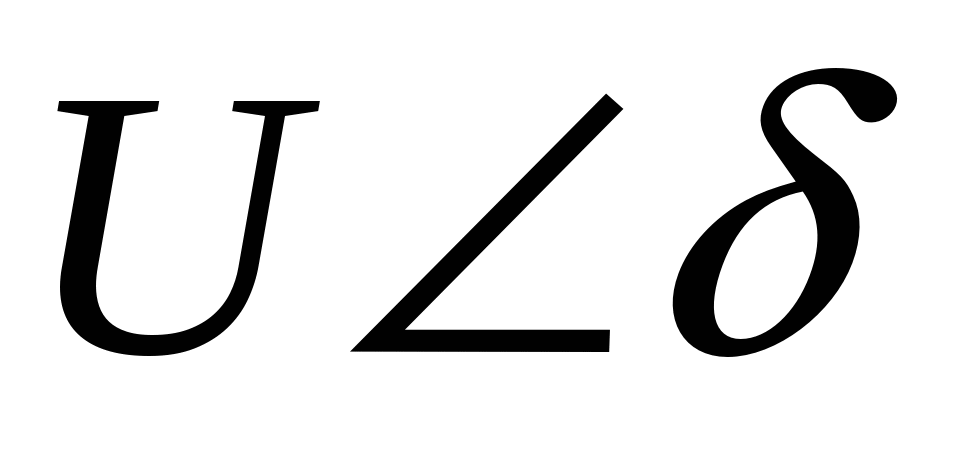 нельзя => переходим от записи в комплексном виде к 2м уравнениям с веществ. коэффициентами.
(n-1) ур-й с компл. → (2n-2) с веществ.
Пр. Метод Ньютона
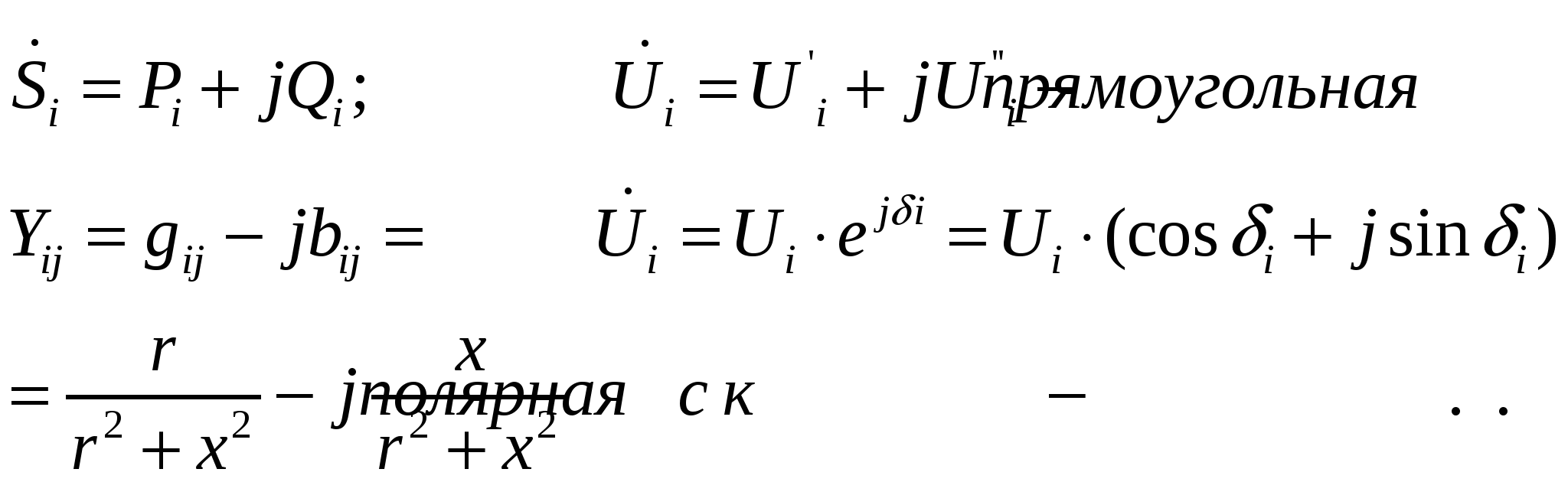
В зависимости от формы записи эффективность методов м.б. различна, т.е может отличаться сходимость и время расчета(кол-во итераций).
|
43’ Узловое уравнение в форме баланса мощности, записанное в прямоугольной системе координат.
  
   
|
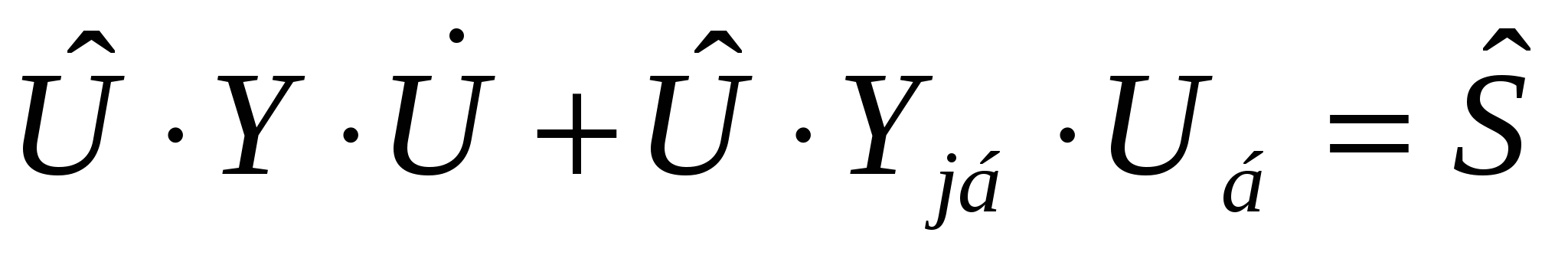
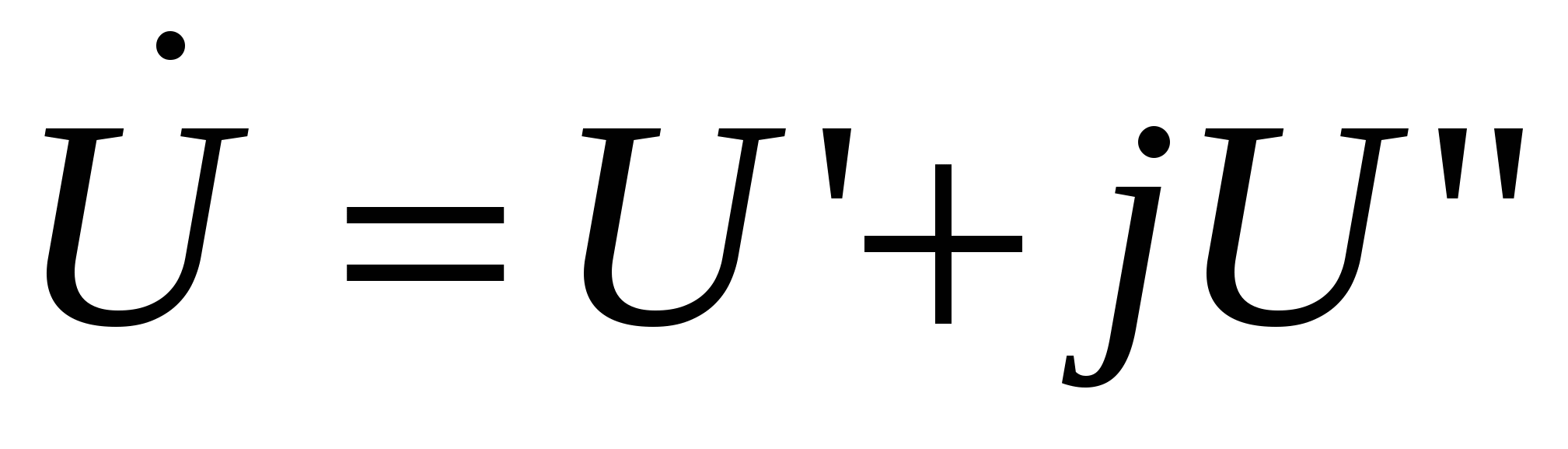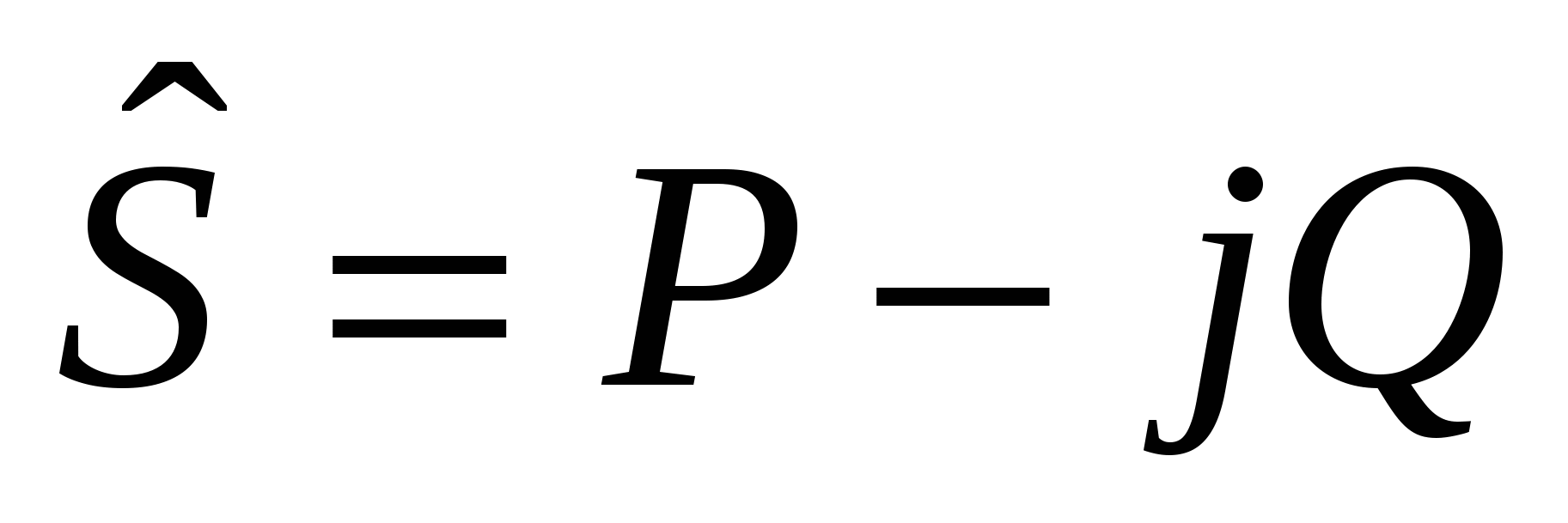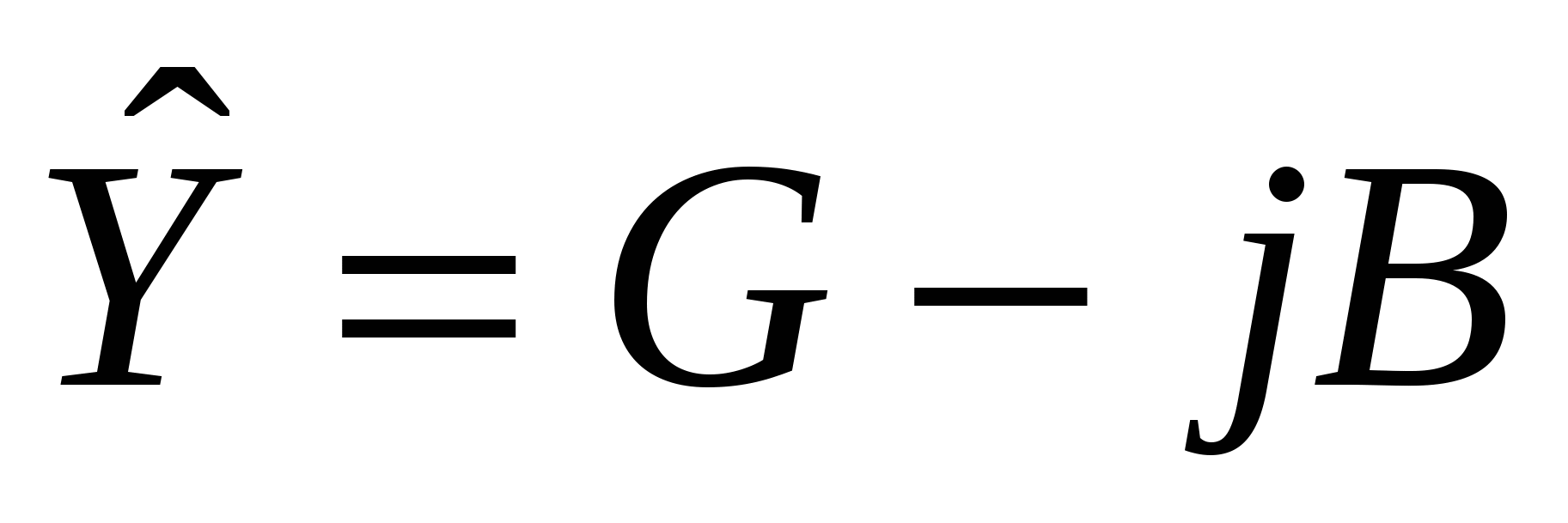
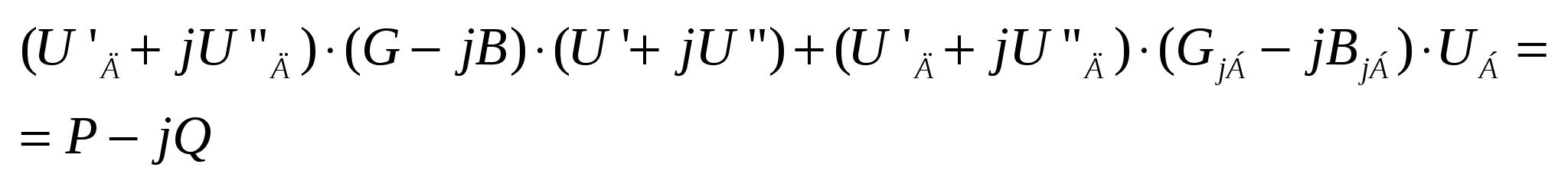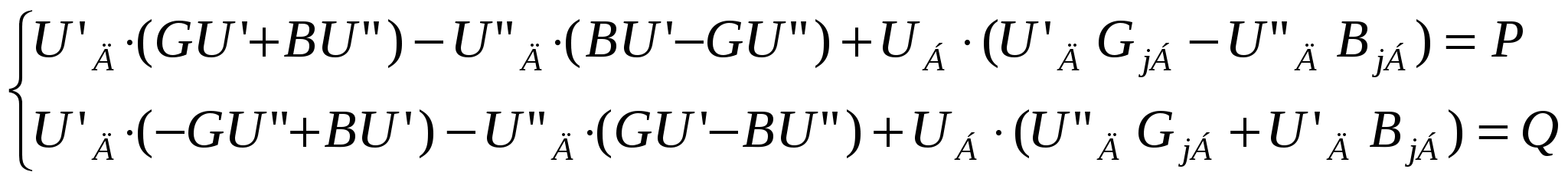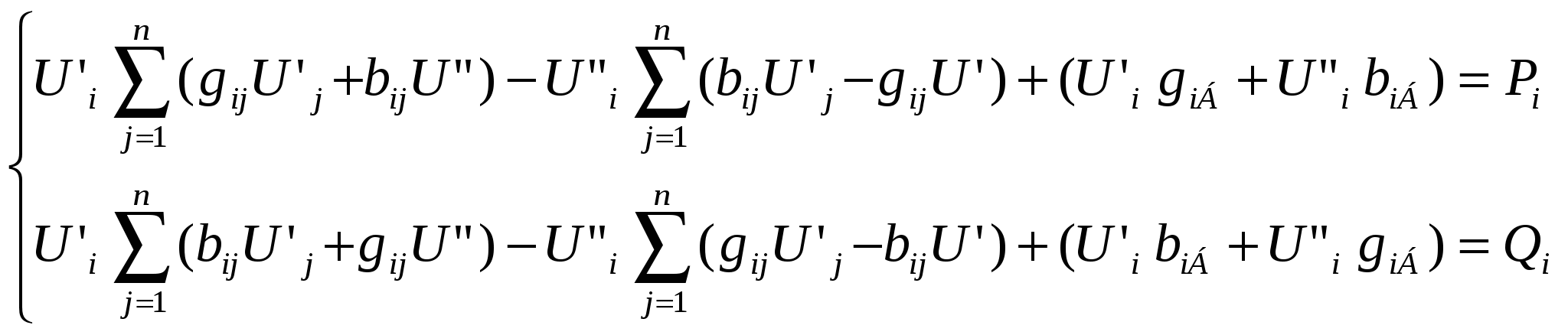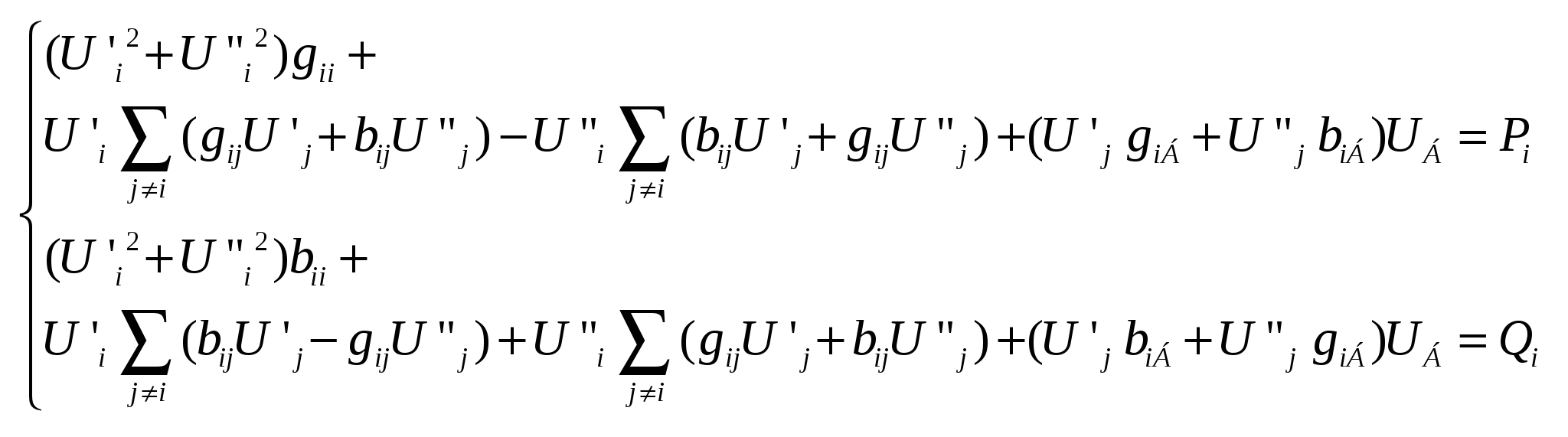
44’ Узловое уравнение состояния эл. сист. в форме баланса S при записи напряжений в полярной, а проводимостей – в прямоугольной системах координат.
|
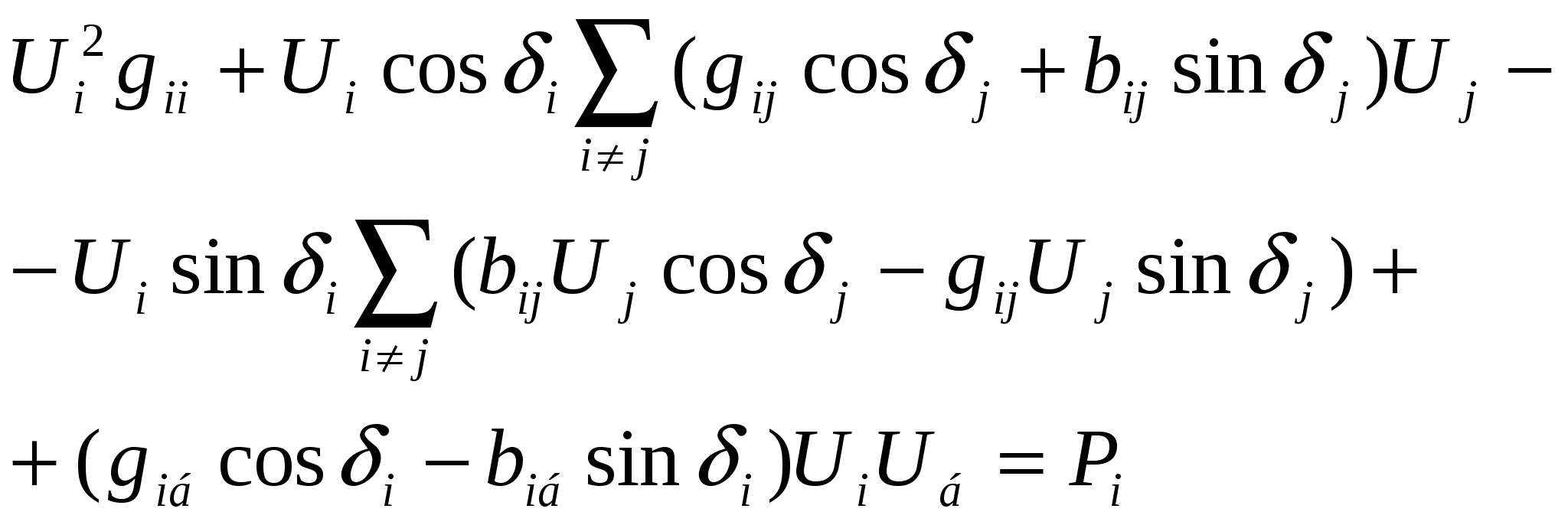
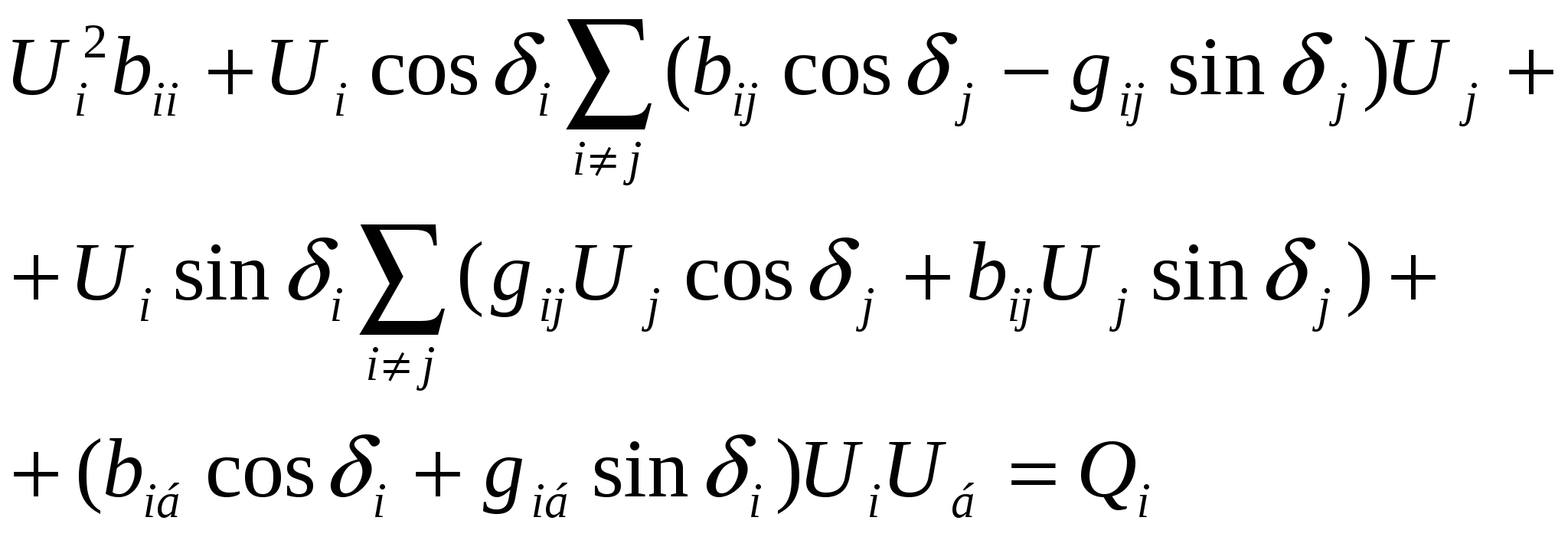
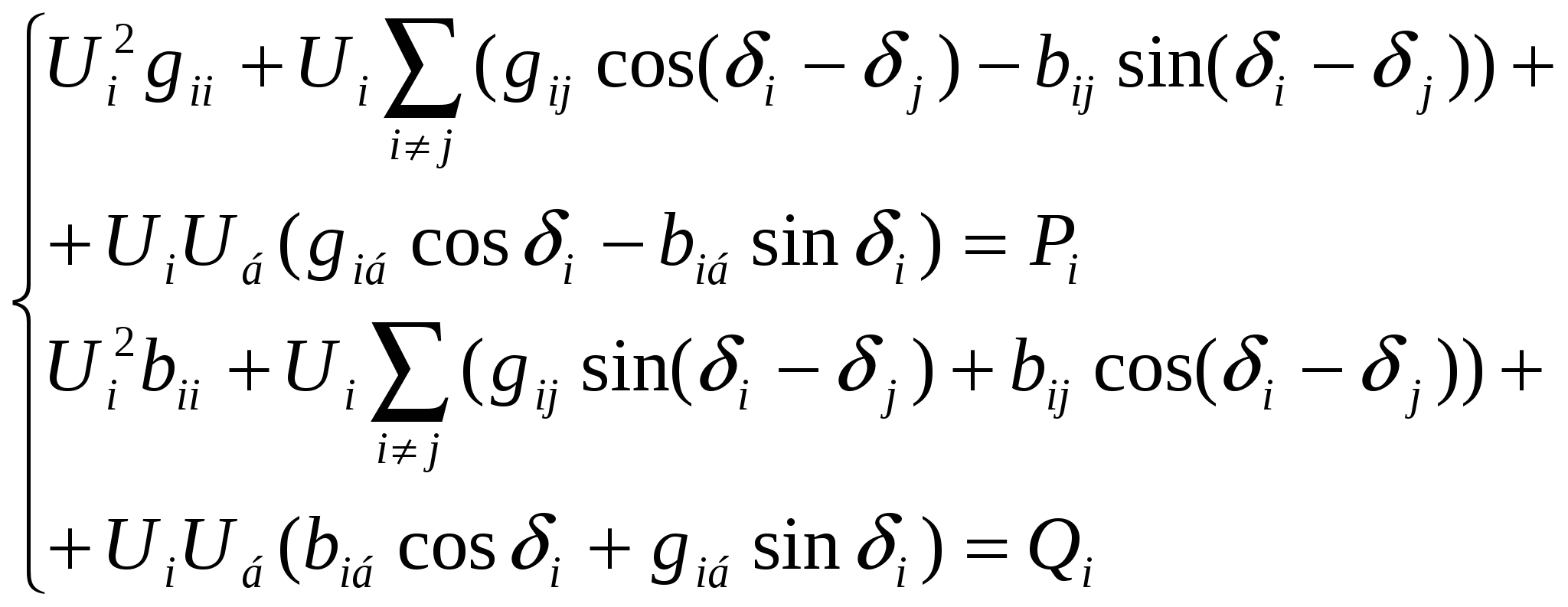
45’ Узловое уравнение состояния эл. сист. в форме баланса мощности, записанное в полярной системе координат.
|
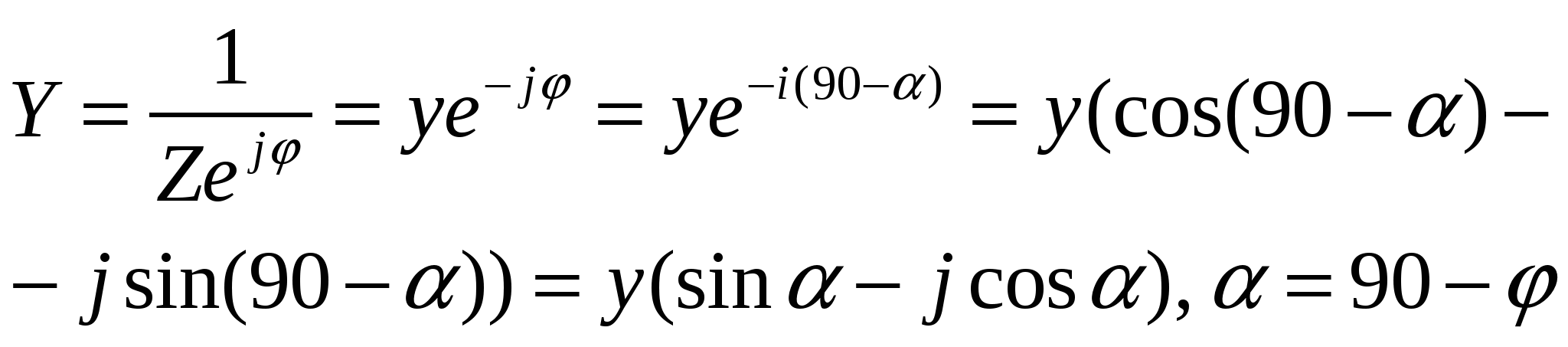
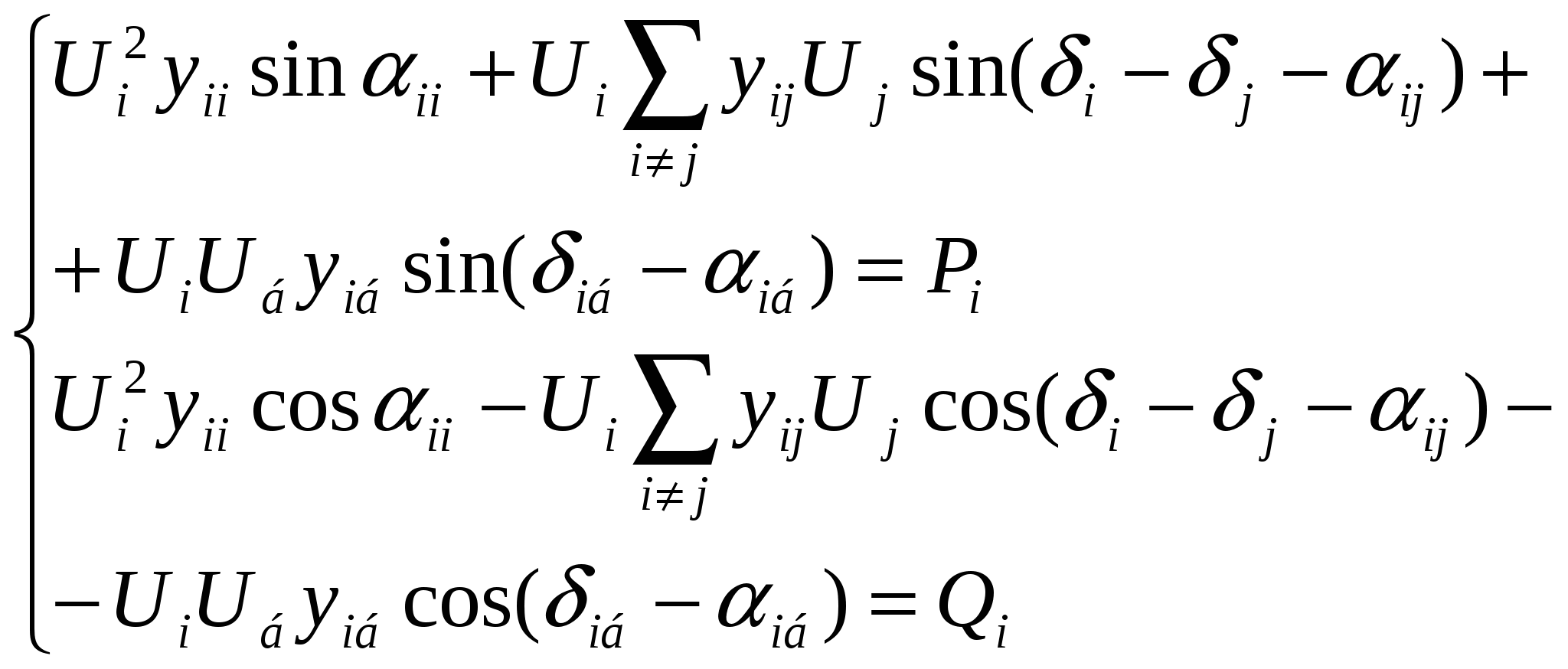
46’ Возможные формы записи нелинейных узловых уравнений установившегося режима для решения их методами, требующими разделения комплексных переменных на действит.сост.
1)узловые уравнения в форме баланса токов в прямоугольной системе координат
2)---//-----//--- в полярной системе координат
3)узловые уравнения в форме баланса мощности в прямоугольной системе координат
4)---//-----//--- в полярной системе координат
|
47’ Метод Ньютона. Решение узлового уравнения методом Ньютона, записанного в прямоугольной и полярной системе координат.
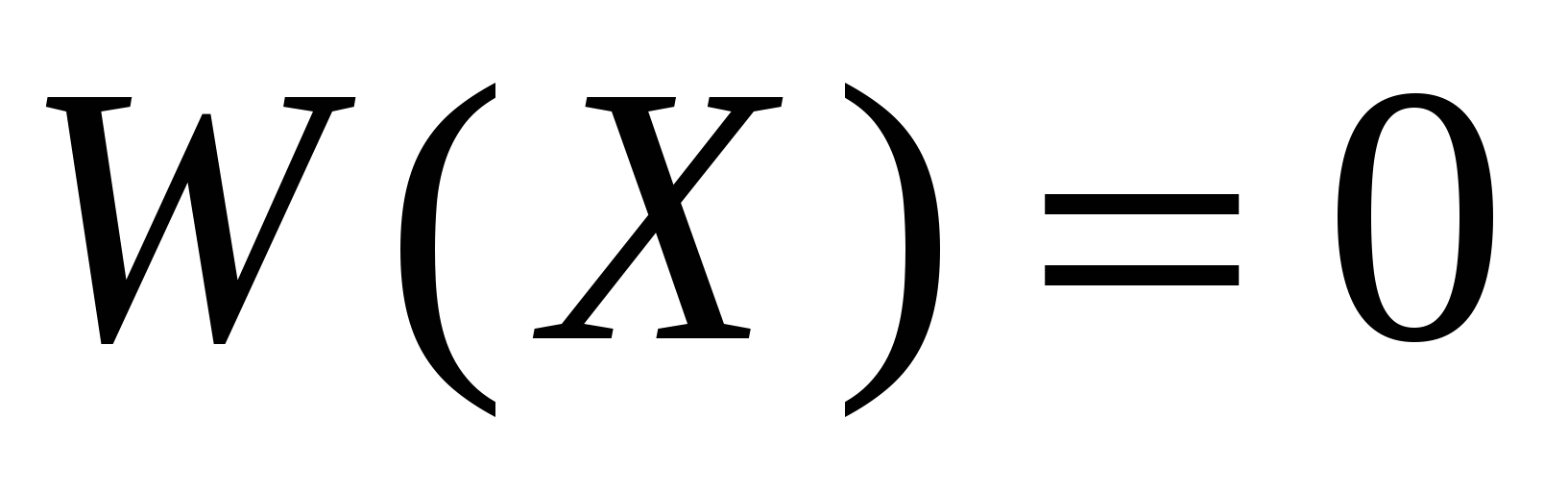
1)Начальные приближения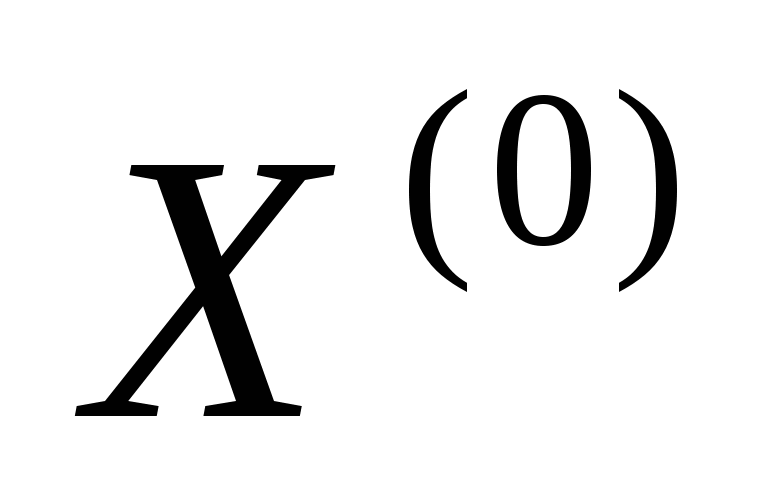 
2)В точке начального приближения данная система линеаризуется путем разложения в ряд Тейлора и отбрасыванием нелинейных частей.
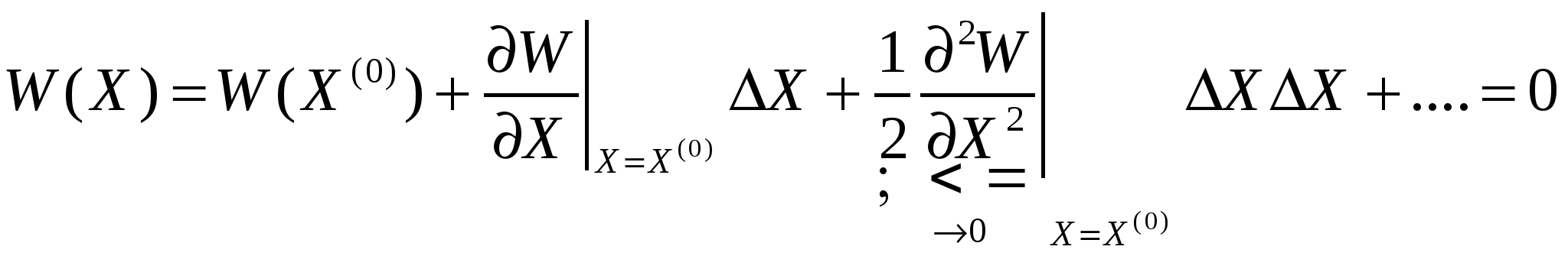
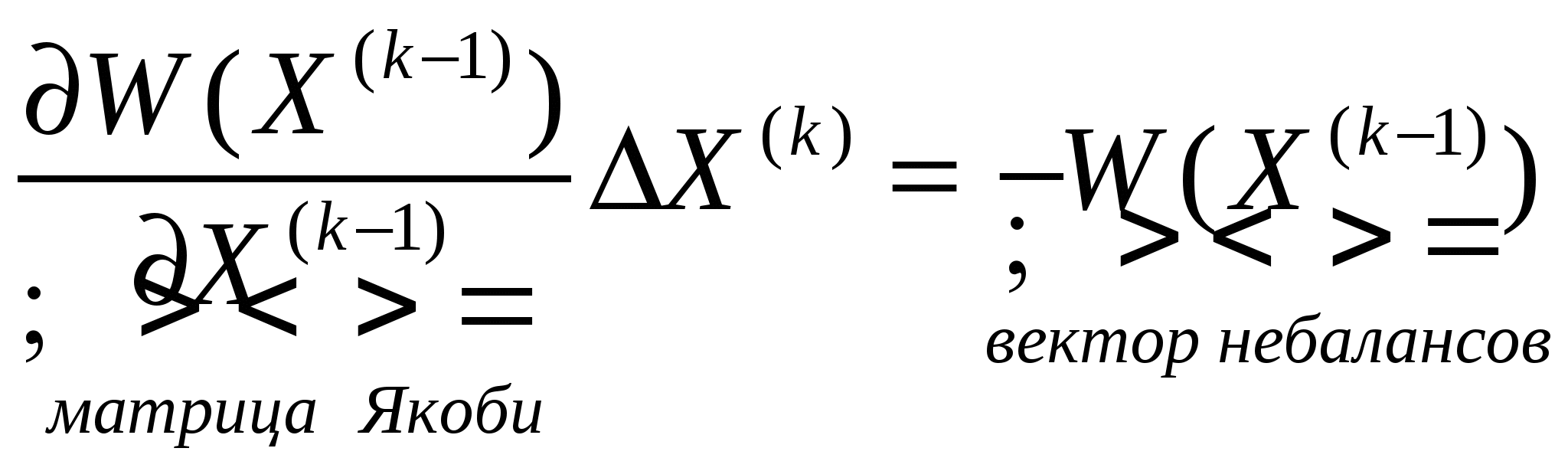
Т.о. метод Ньютона сводится к многократному решению (на каждой итерации) СЛАУ.
3)
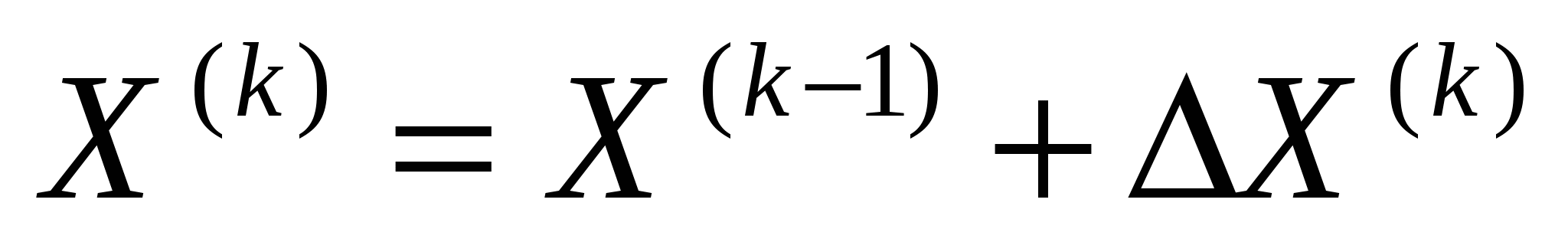
Прямоуг. сист. коорд.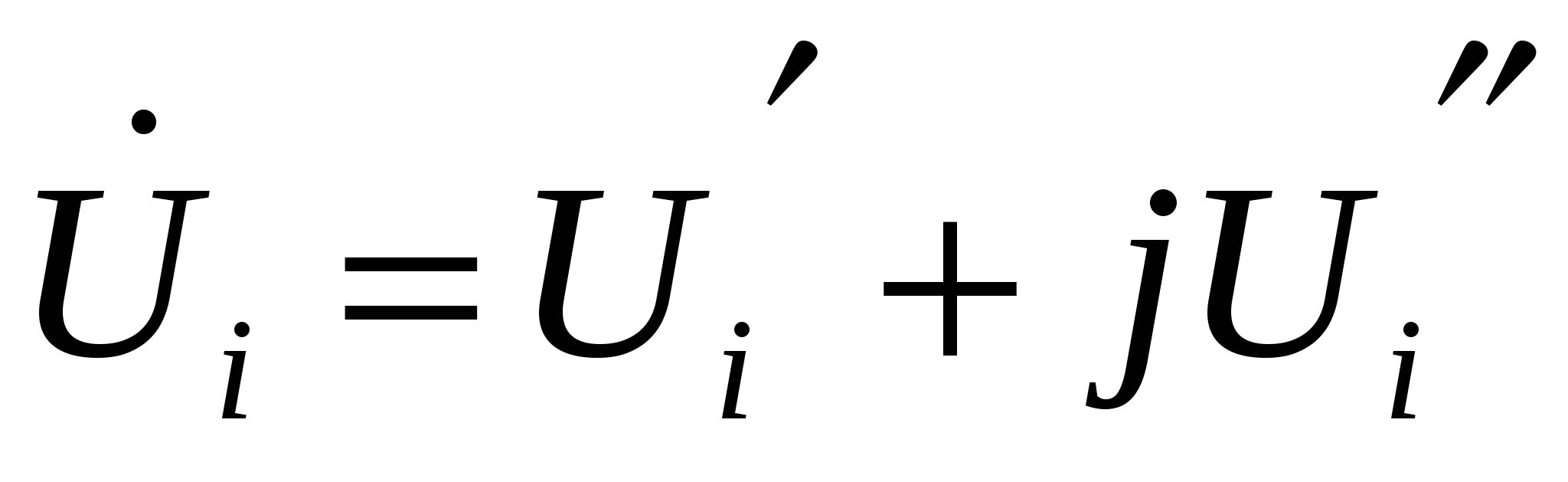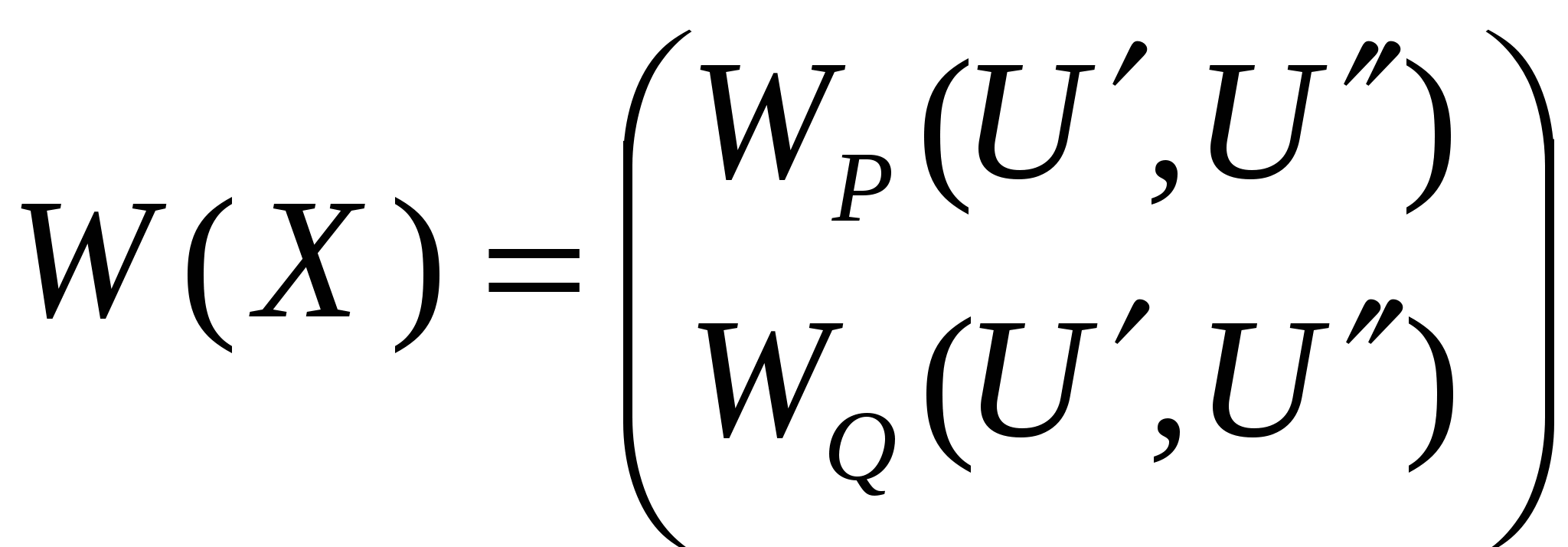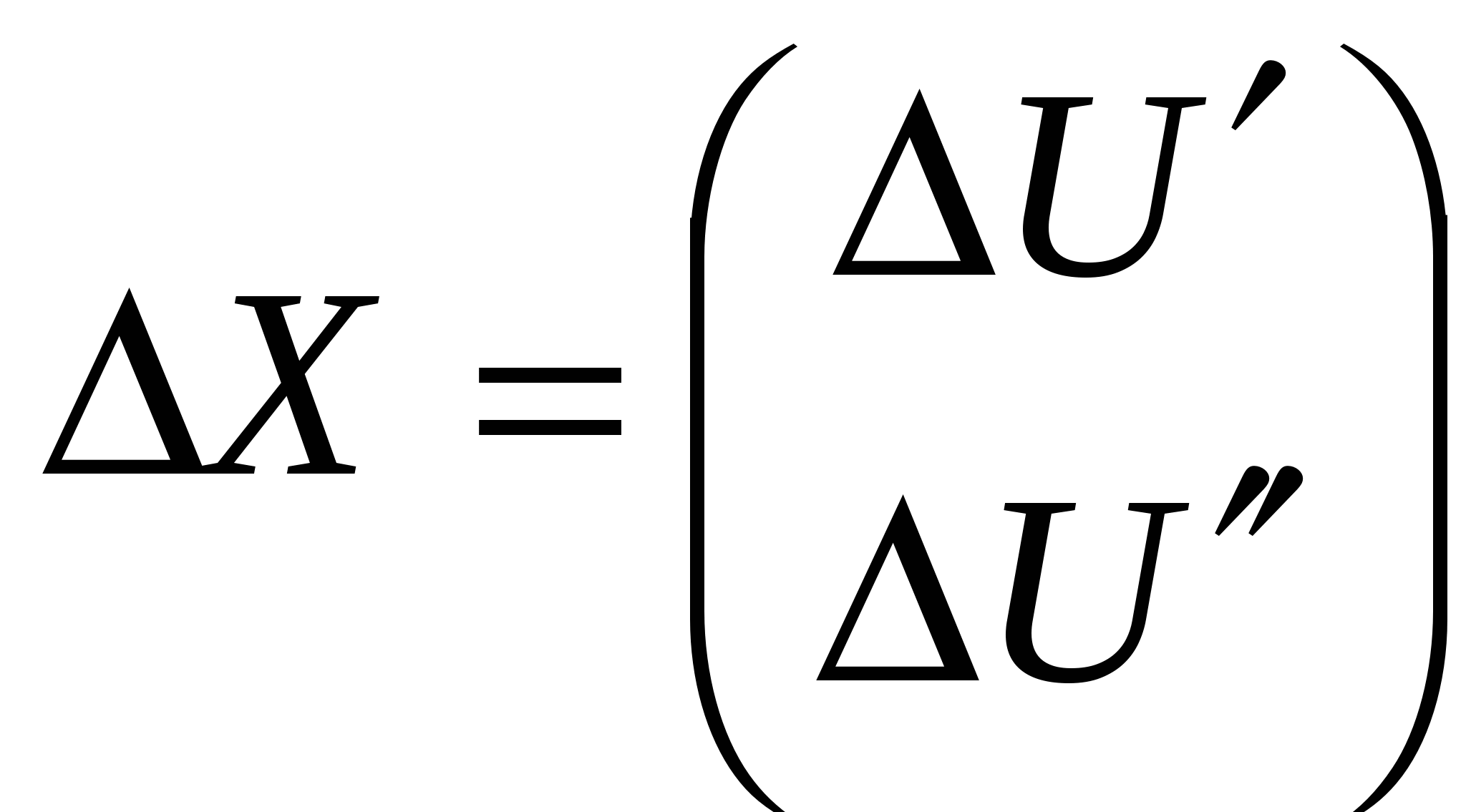   
Полярная  ;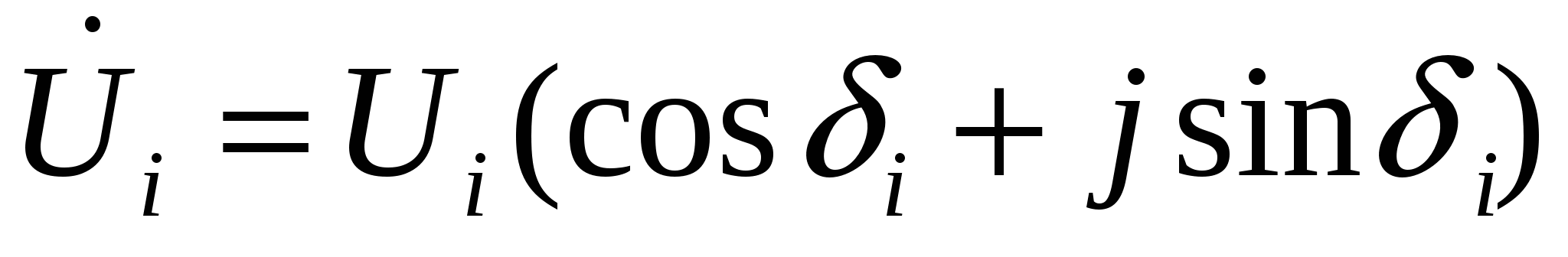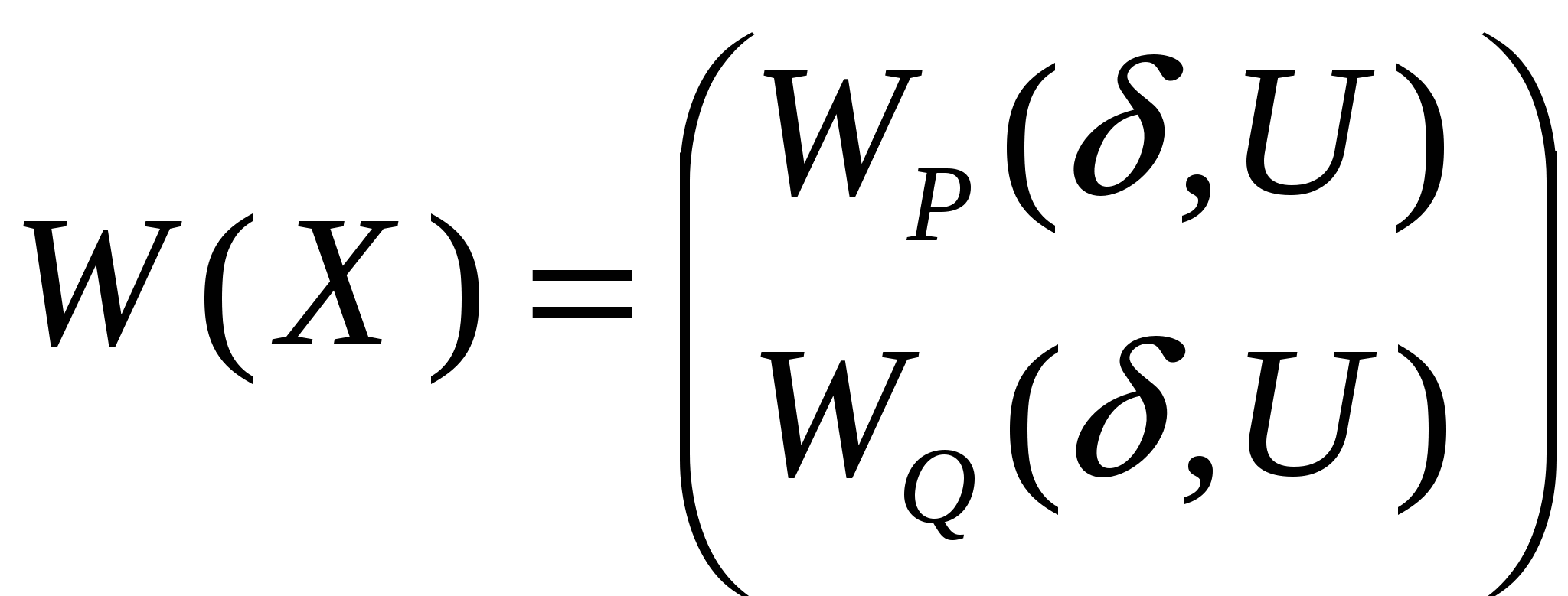 
|
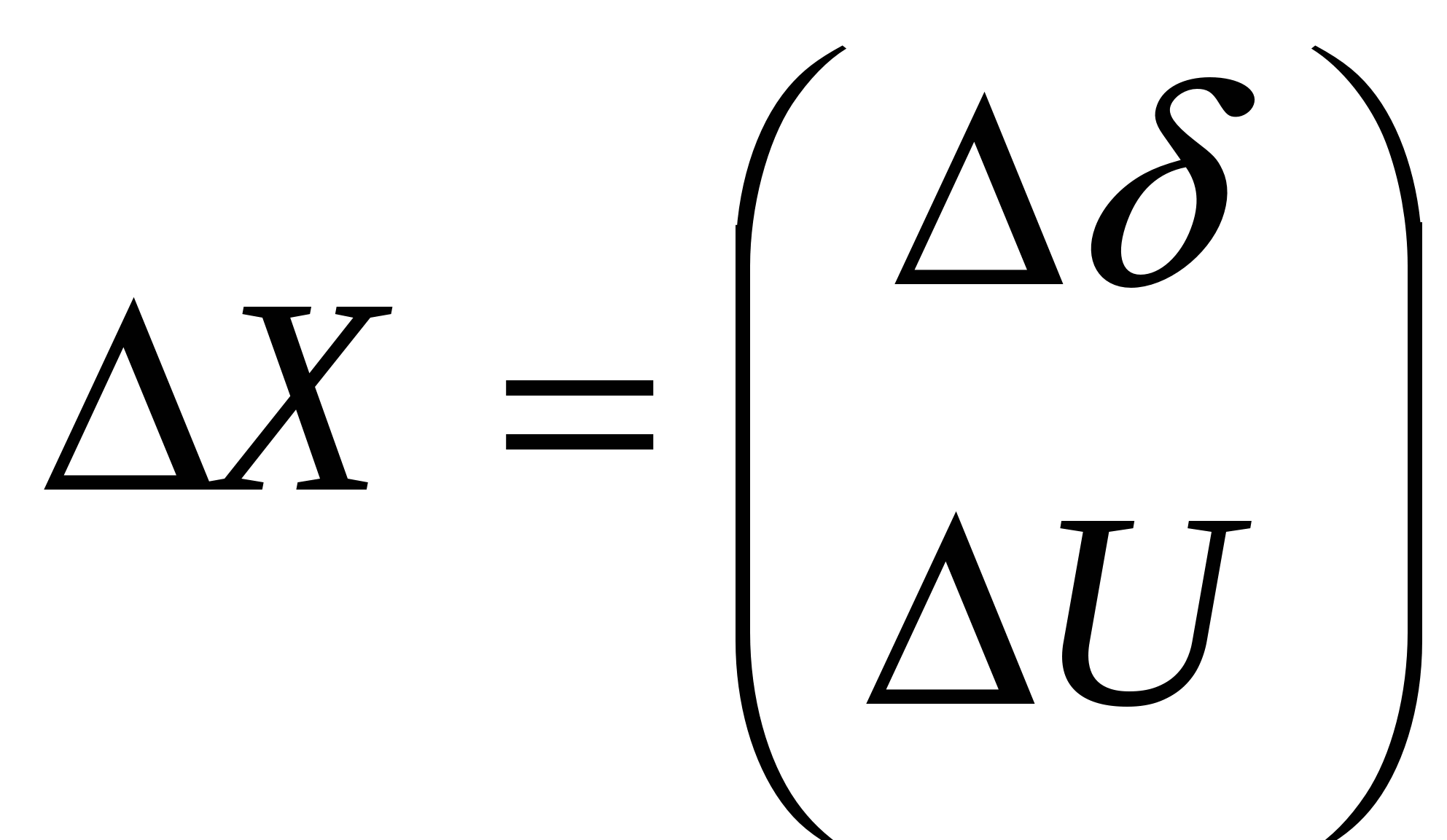
48’/49’ 3ависимость размерности матрицы Якоби от формы представления генераторных узлов и системы координат, в которой записаны узловые уравнения в форме баланса мощности.
|
Неопорный Рг, Qг
|
Опорный Pг,Uг
|
 ,
|
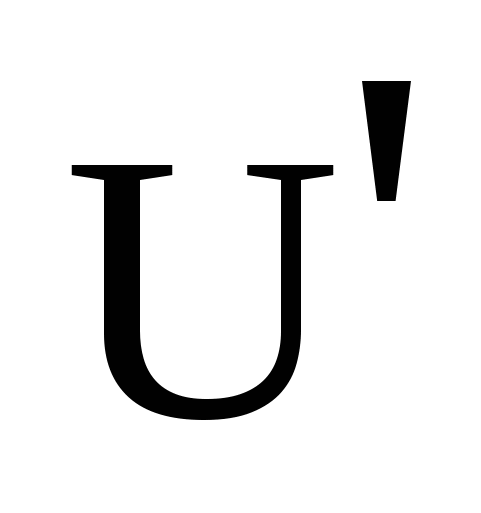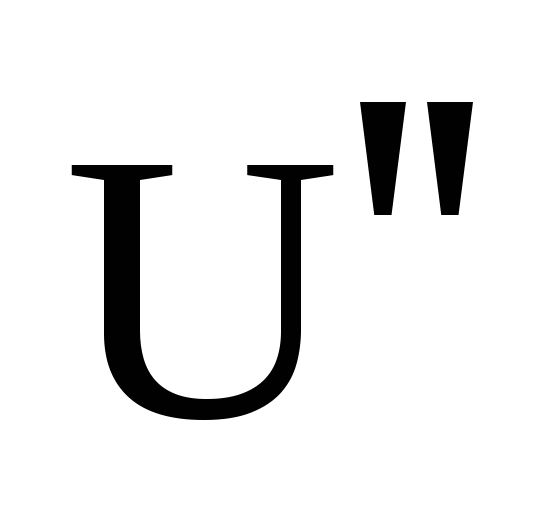
2(n-1) х 2(n-1)
|
2(n-1) х 2(n-1)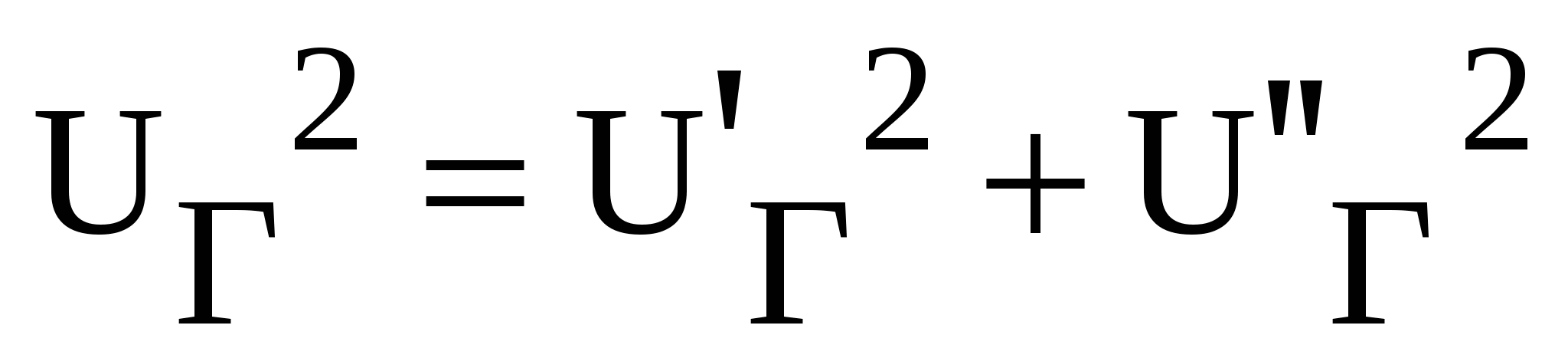 
|
U,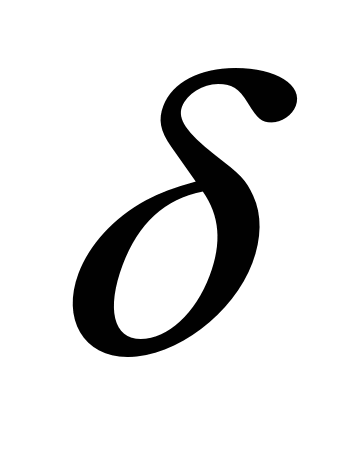 
|
2(n-1) х 2(n-1)
|
[2(n–1)–k] х[2(n–1)–k]
|
Опорные: k- опорных узлов
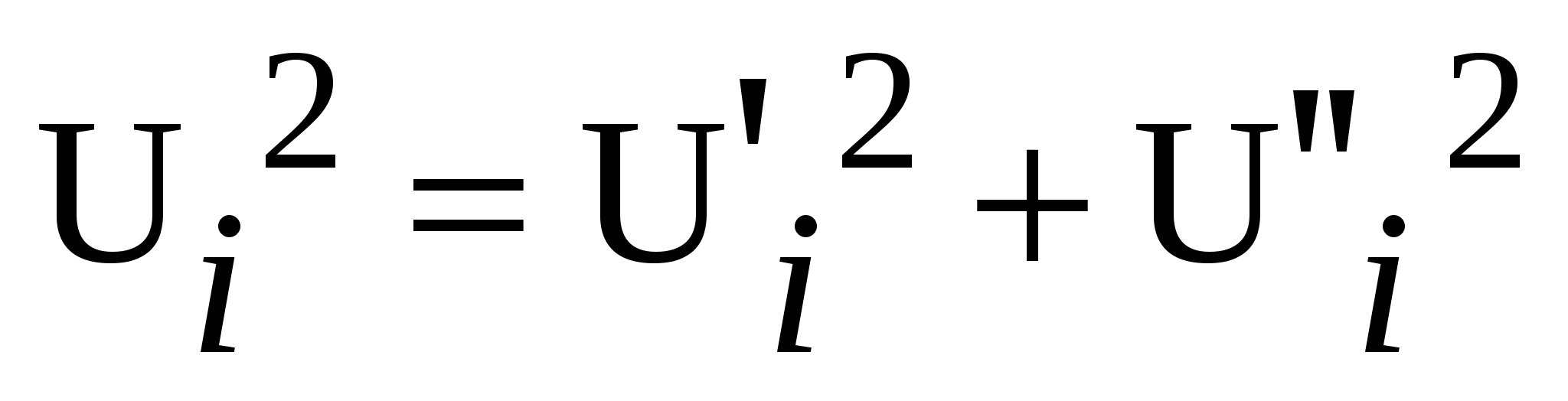 - входит в уравнение баланса Q
Вывод: При опорных генераторных узлах кол-во уравнений в полярной форме снижается (при решении уравнения в форме баланса мощности)
|
50’ Аналитическое выражение элементов матрицы Якоби узловых уравнений в форме баланса мощности, записанных в полярной системе координат.
При решении уравнений установившегося режима, записанных в форме баланса мощности, предпочтительным является решение в полярной системе координат:
 
|
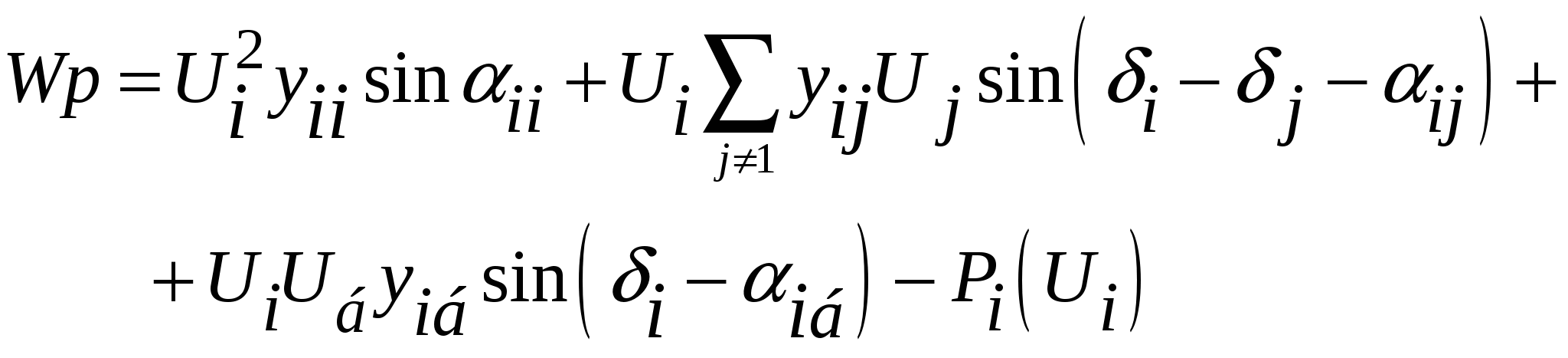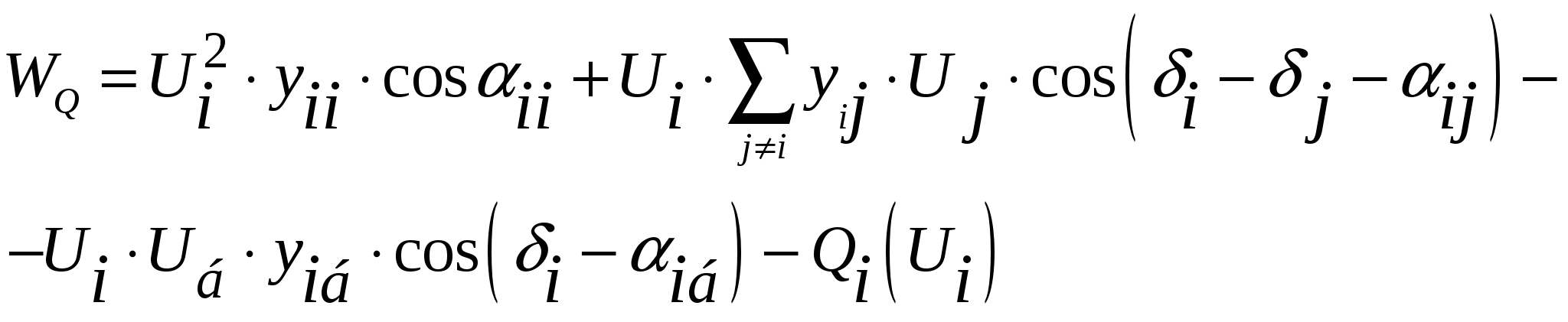
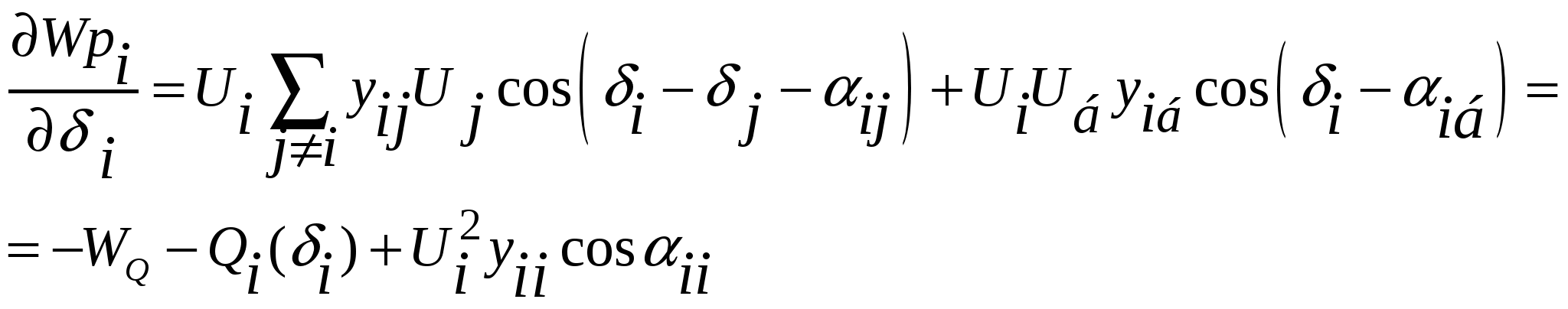
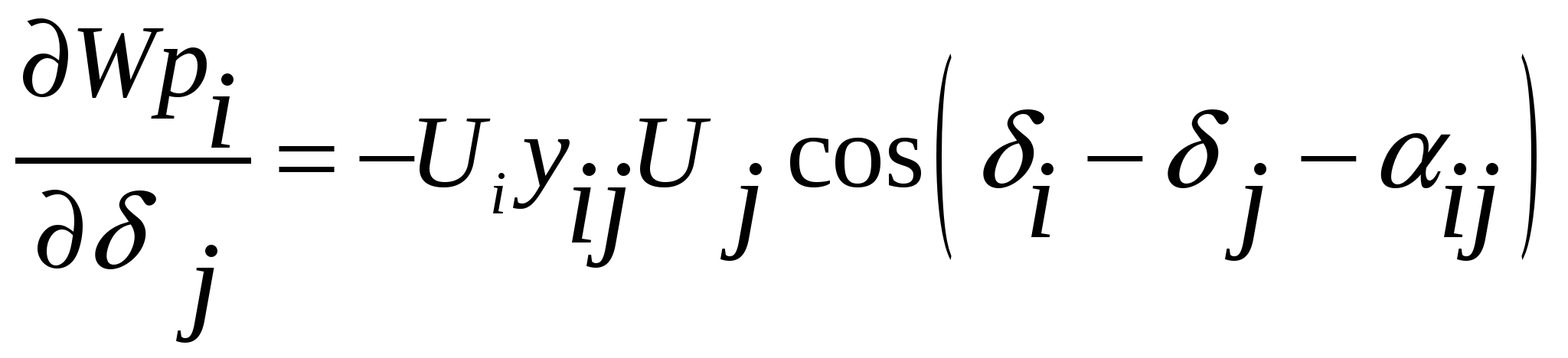
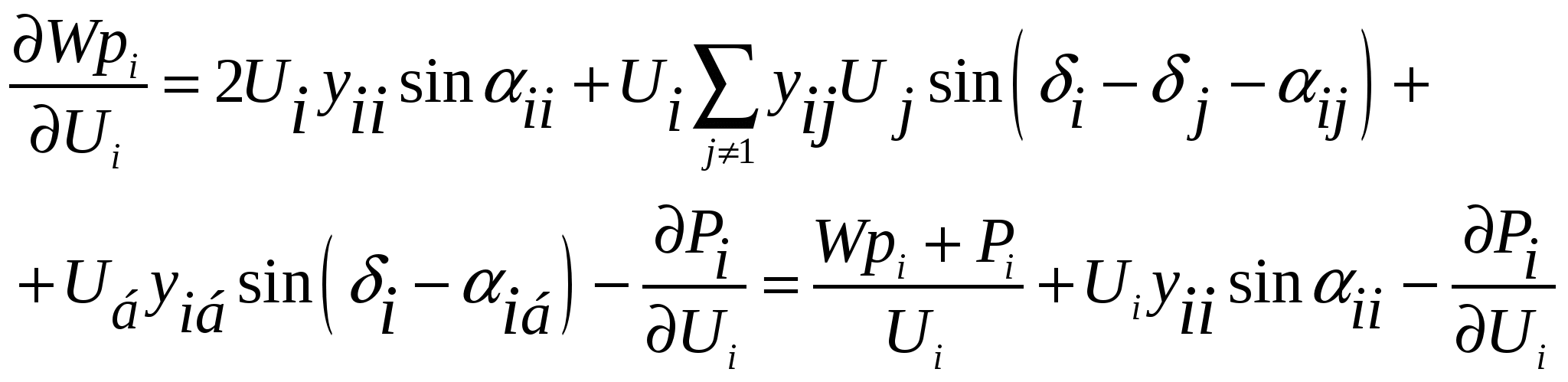
50’ Продолжение.
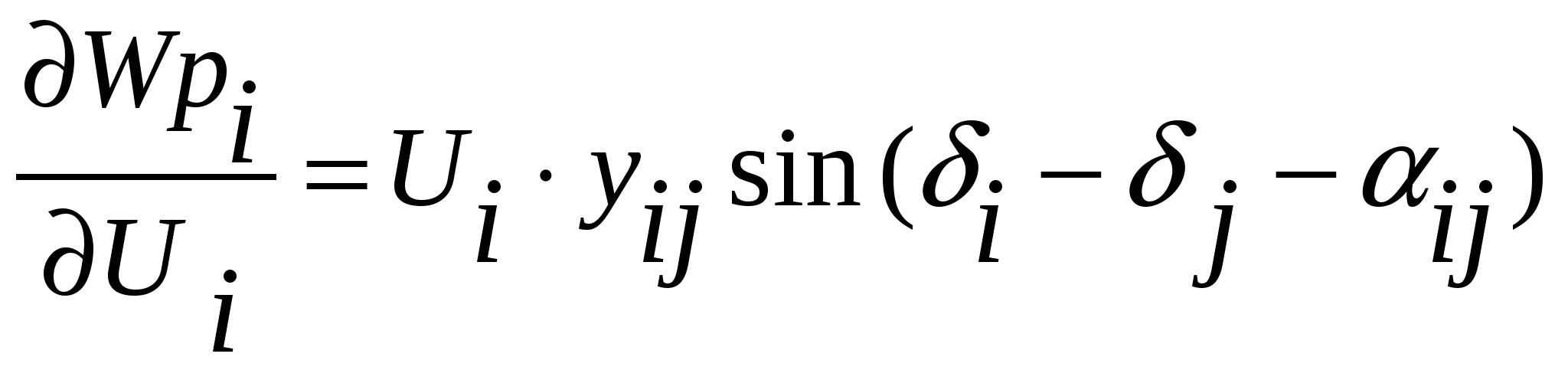
Аналогично,
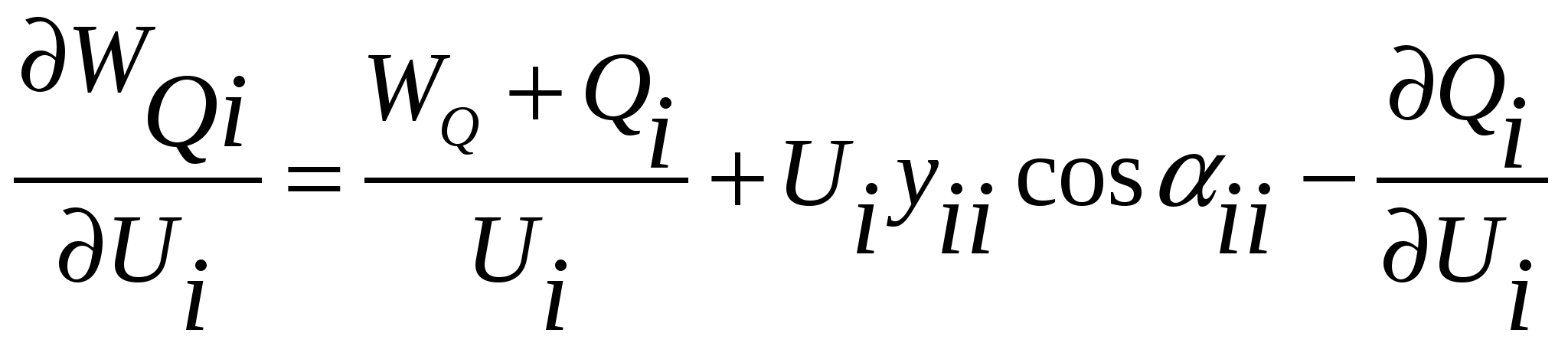
С билетом тебе не повезло. Улыбайся преподу
|
51’ Свойства матрицы Якоби. Свойства метода Ньютона.
Св-ва матрицы Якоби:
1) Слабозаполненная
2) Структурно-симметричная, но числовой симметрии нет:
Структурная симметрия облегчает учет слабой заполненности, поиск и хранение ненулевых элементов.
3) Диагонально-доминирующая: Св-ва совпадают со св-вами м.Y
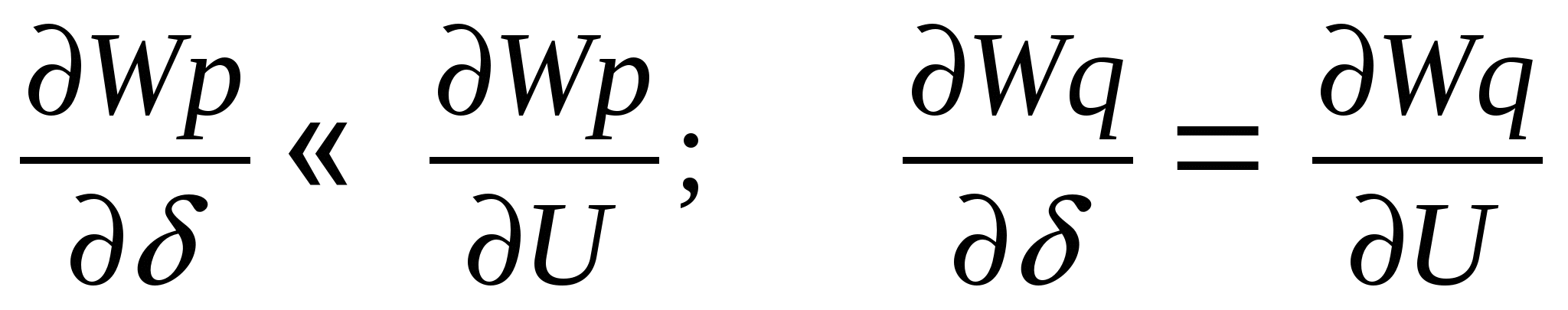
Св-ва матрицы Ньютона:
1) Сильная чувствительность к начальным приближениям.
2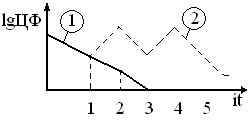 ) Квадратичная сходимость
 
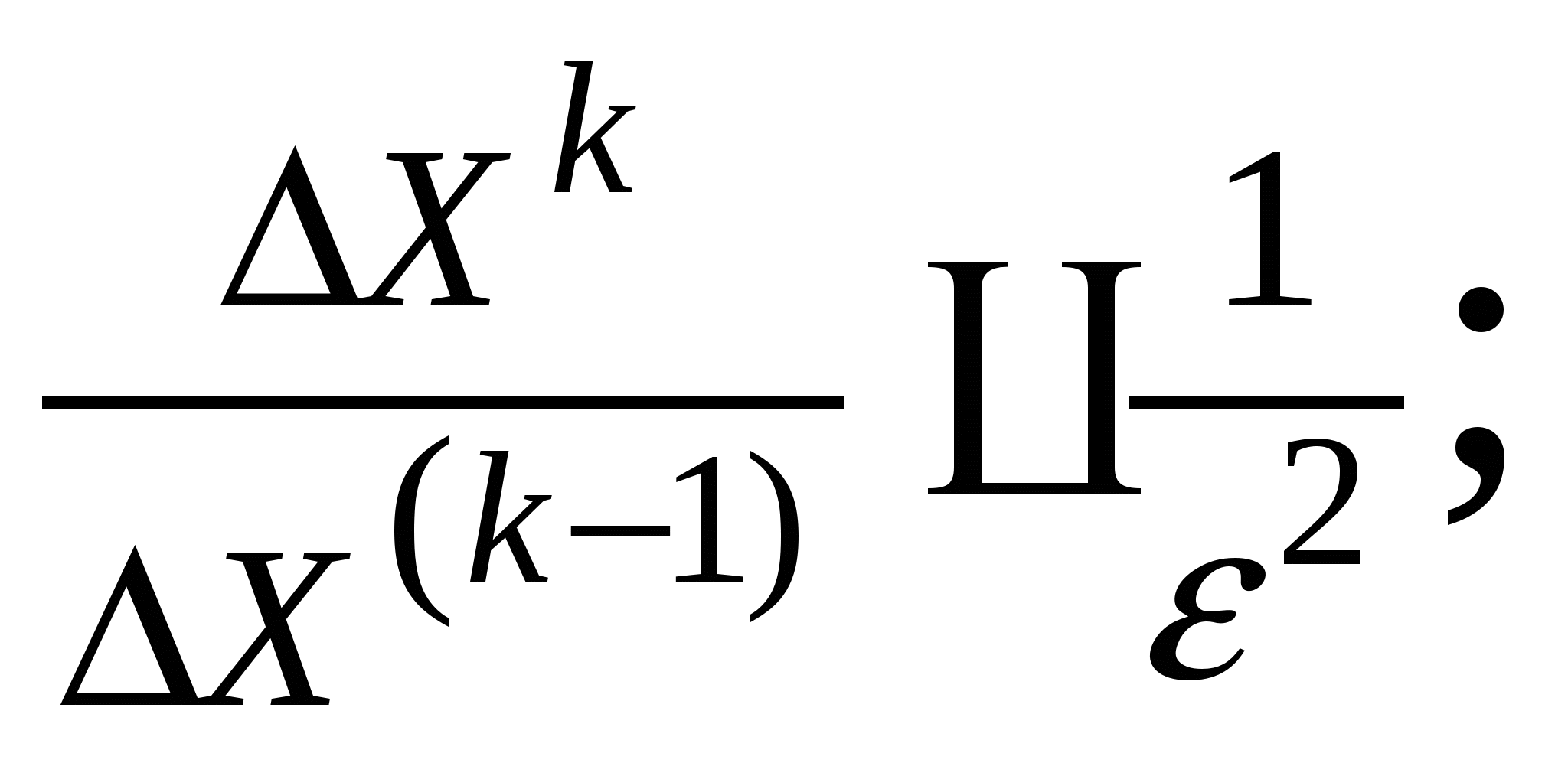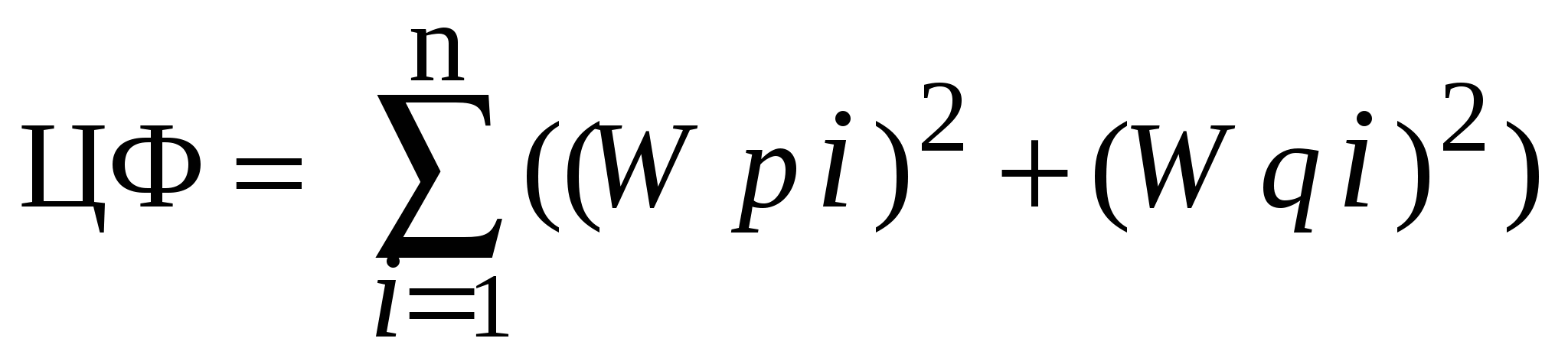
1. При отсутствии активных ограничений:
– Наличие резервов акт. и реакт. мощности, – Большой Кз по статической устойчивости, – Отсутствие перегрузок по линиям
2.При наличии активных ограничений:
– Дефицит Q, – Предел по станциям (вышли на ограничения по генерат. узлам), – Pг, Uг,  Pг,Qг
3.Сходимость может ухудшиться при плохой обусловленности матрицы Якоби
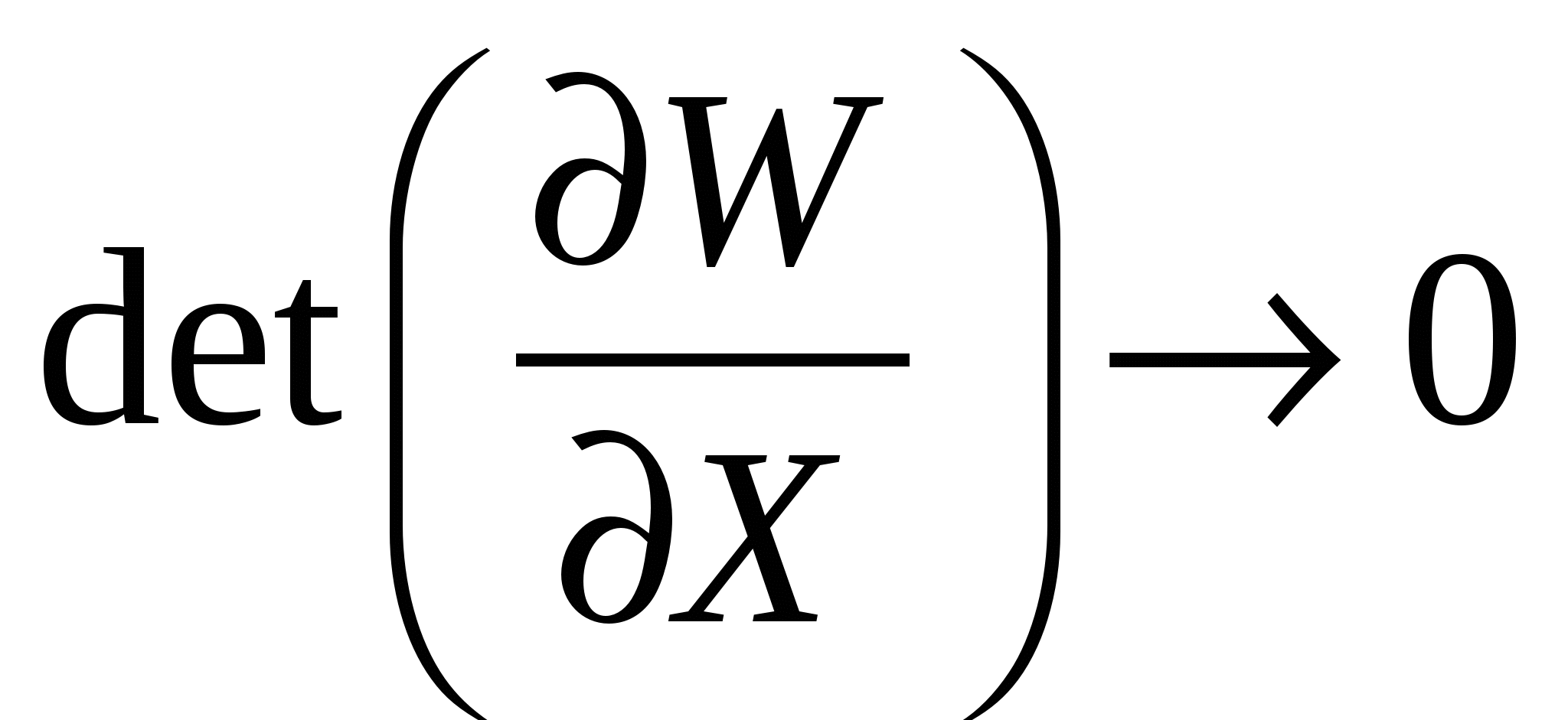
(режимы, близкие к пределу по статике; резко неоднородная сеть)
4.Погрешности исходных данных влияют на сходимость метода Ньютона, решение системы уравнений по Гауссу.
5.Хорошо согласуется с методами решения оптимизац-ых задач.
6.Трудоемок в части алгоритмического представления.
|
52’ Модификации метода Ньютона
Метод Ньютона основан на решении всех уравнений системы на каждой итерации, это повышает вычислительную эффективность. Применение этих методов требует перехода от (n-1)-го уравнений с комплексными к (2n-2)-м ур-ям с вещественными коэффициентами и переменными. Это связано с тем, что применение этих методов требует диффер. ур-й по искомым переменным (а производные по комплексным переменным не определены). Кроме того, для общего случая задания оп. генер. узлов (P, U), искомые переменные Q, δ– вещественные. Переход осуществляется на основе записи компл. чисел в прямоуг. или полярной системах координат.
1) В мет. Н с обращением матрицы Якоби СЛАУ решается на каждой итерации относительно вектора приращения независимых перем. с использованием обратной матр. Якоби:
|
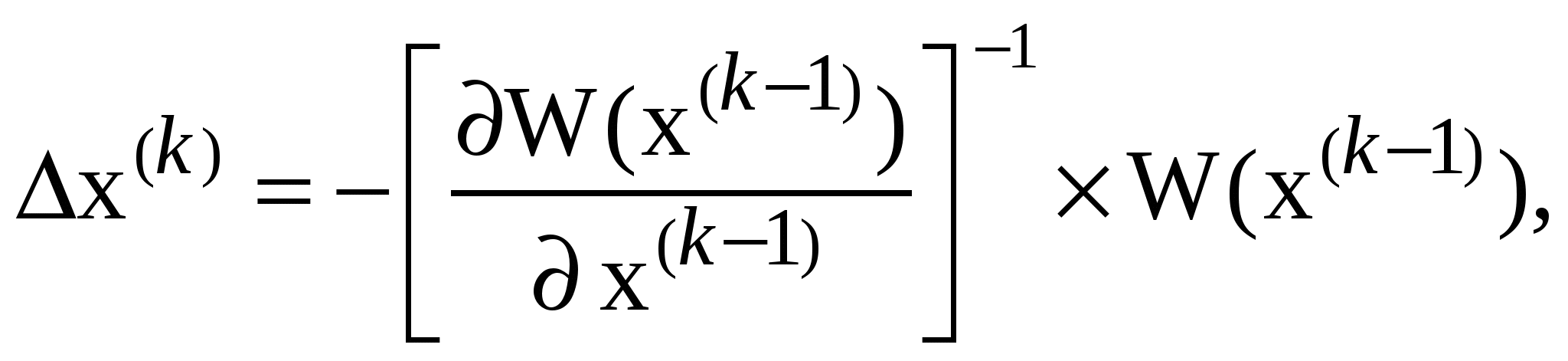
значения на каждой ит. можно опред. по выражению:
|
|
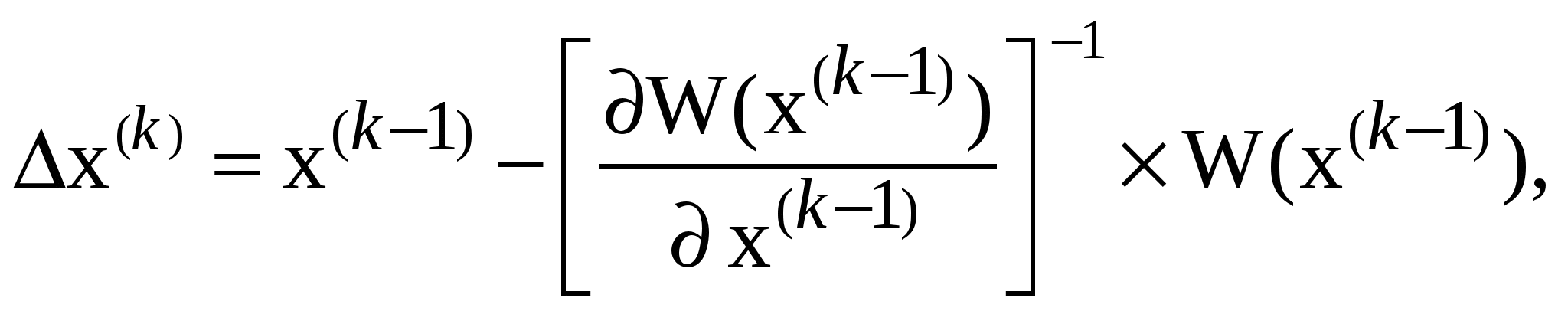
[ 1]
|
[ 2]
2) Введение параметра t(0< t <1)т.е. переход от итер. формулы [ 1 ] к выражению [ 2 ] есть переход к мет. Н. по параметру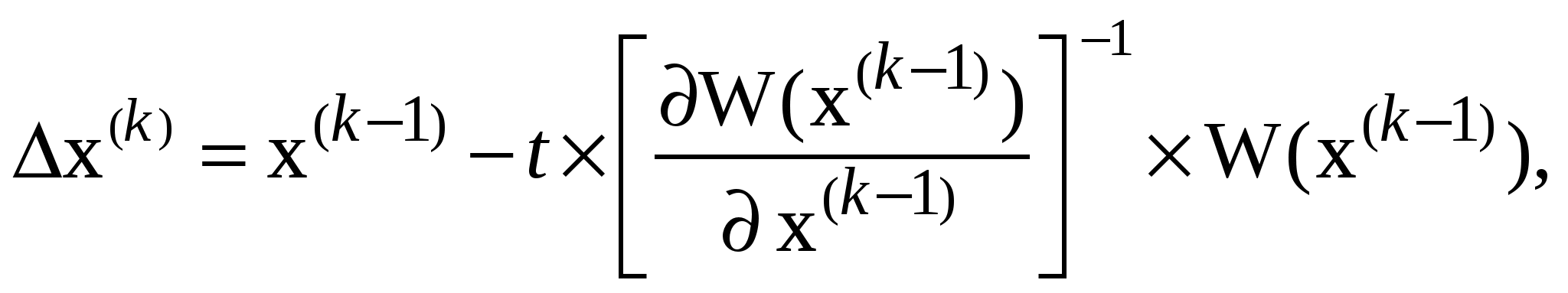 
3) С разделением параметров (блочная диагонализация). Существенно уменьшает объем расчетов на ит., из-за отбрасывания недиаг. блоков матр. Якоби, т.е. полагая ∂P/∂δ=0 и ∂Q/∂δ=0 (см.55’)
4) Модифицированный – матрица Якоби вычисляется только 1 раз.
|
53’ Модифицированный метод Ньютона. Сущность и область
сходимости.
Основан на том, что если Δx (k) → 0, то и ΔW(x (k–1)) → 0, т.е. можно вычислять матрицу Якоби 1 раз.
Эту матрицу можно однократно факторизовать и использовать в процессе итераций в факторизованном виде, что значительно уменьшает объем вычислений на каждой итерации.
Особенность: из-за невысокой сходимости этот метод применяется только для нетяжелых режимов.
|
54’ Метод Ньютона по параметру. Сущность и область метода.
Введение параметра t (0< t <1) т.е. переход от итерационной формулы к выражению ниже есть переход к мет. Н. по параметру (при t=1 – простой мет. Н)
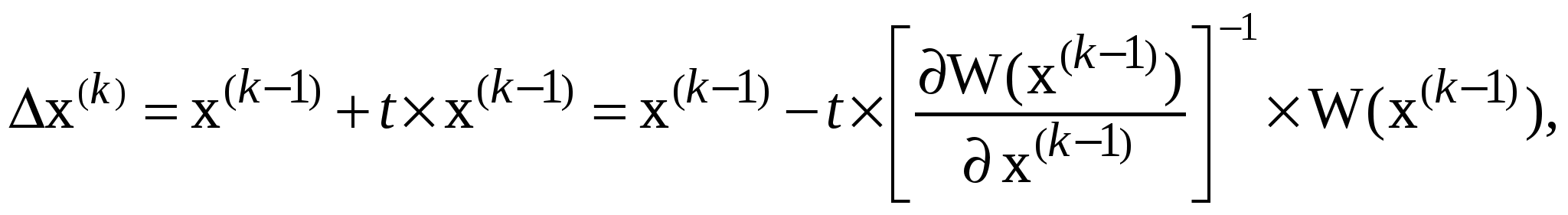 Данный метод применятся для расчетов режимов близких к пределу по статике.
Если
|
|
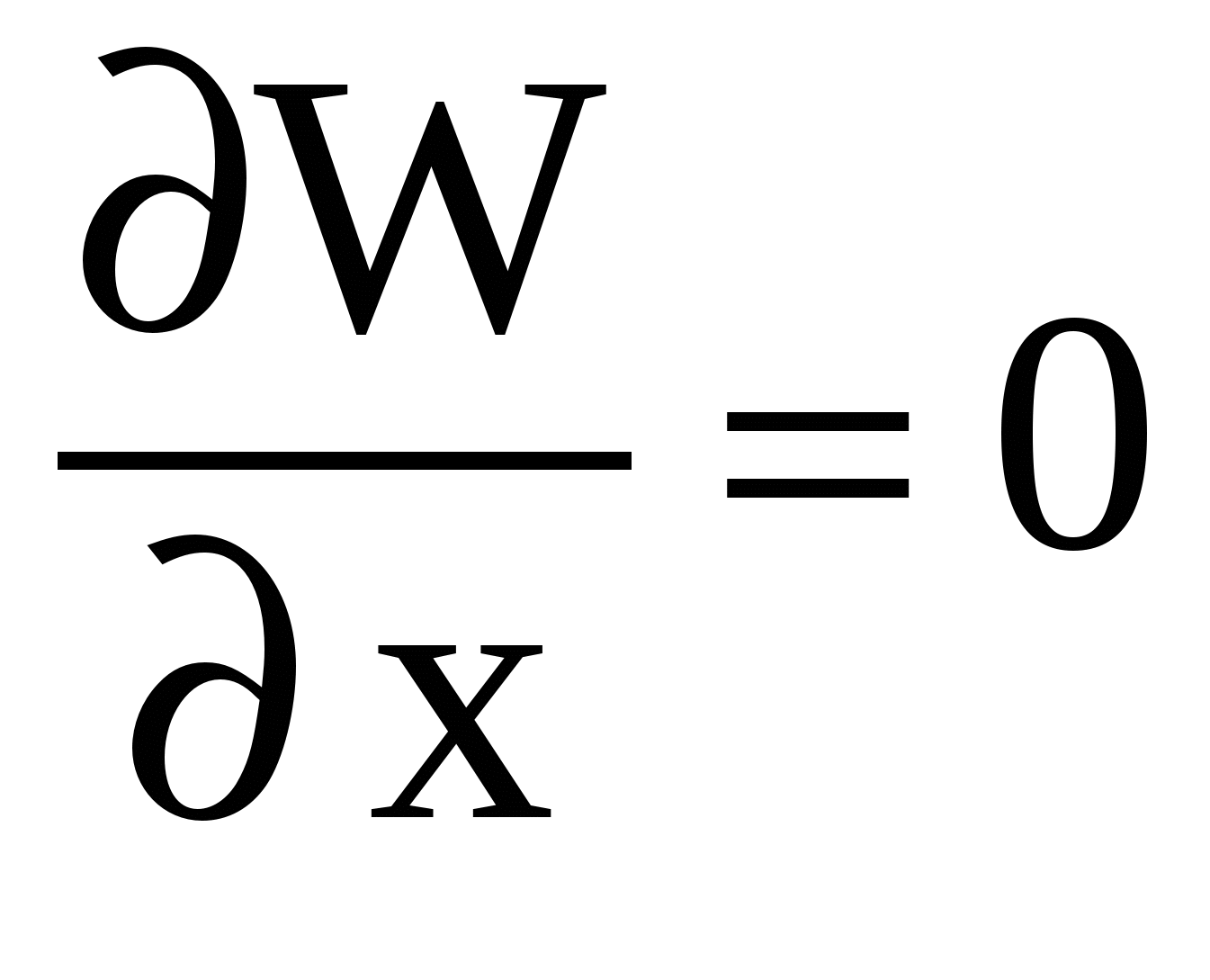
то решений нет.
|
Область сходимости выше чем у обычного метода Ньютона.
Недостаток – большой объем вычислений по итерации: вычисление элементов матрицы Якоби и вектора небалансов, решение СЛАУ
| | |
|
|
Скачать 2.65 Mb.
