Алгоритмы - шпоры (Final). 1 Области рационального использования средств вт. Характеристики каждой из областей

Название	1 Области рационального использования средств вт. Характеристики каждой из областей
Анкор	Алгоритмы - шпоры (Final).doc
Дата	14.05.2018
Размер	2.65 Mb.
Формат файла
Имя файла	Алгоритмы - шпоры (Final).doc
Тип	Документы #19216
страница	2 из 6

1 2 3 4 5 6

15-16’ Учет трансформаторных связей при формировании матрицы узловых проводимостей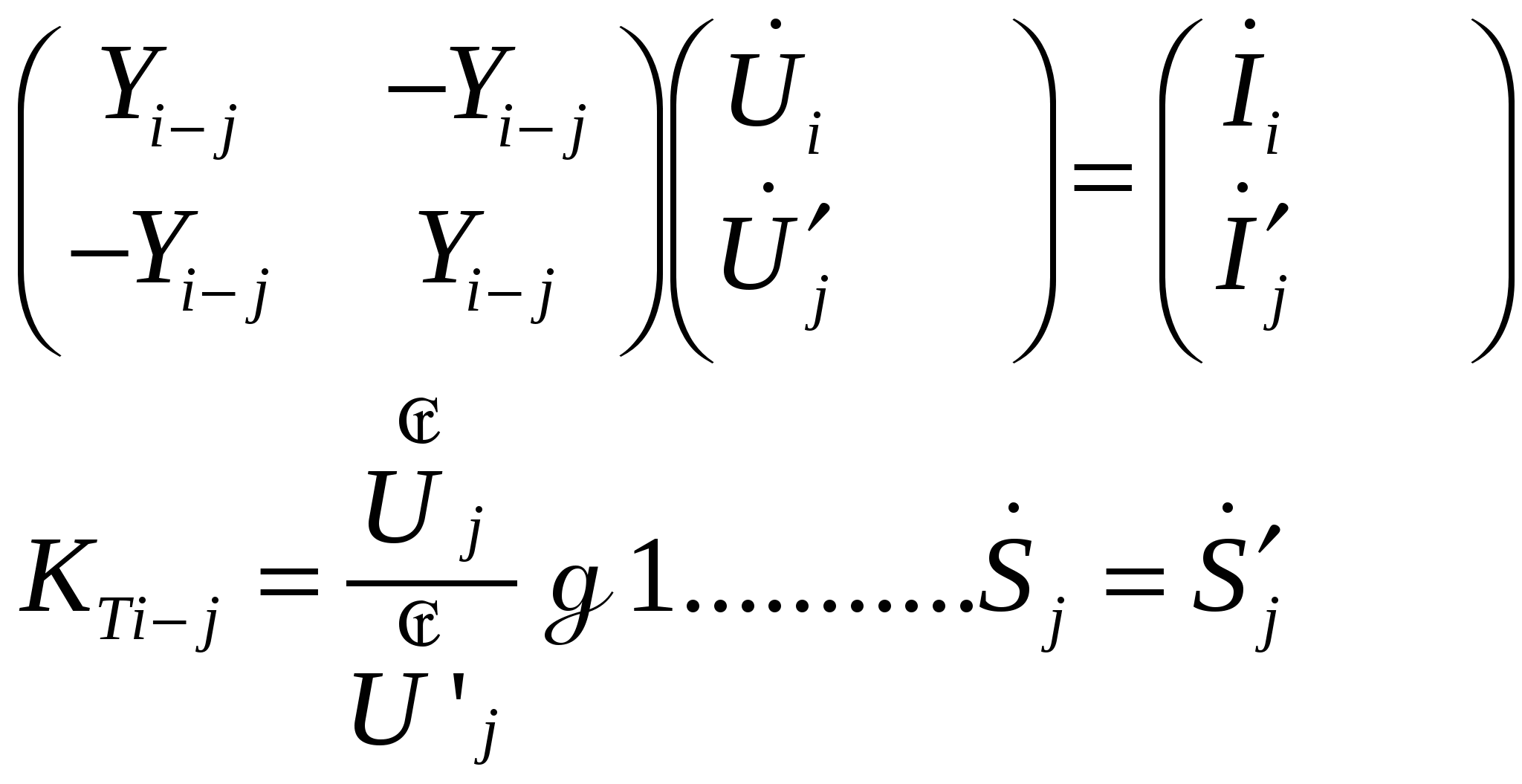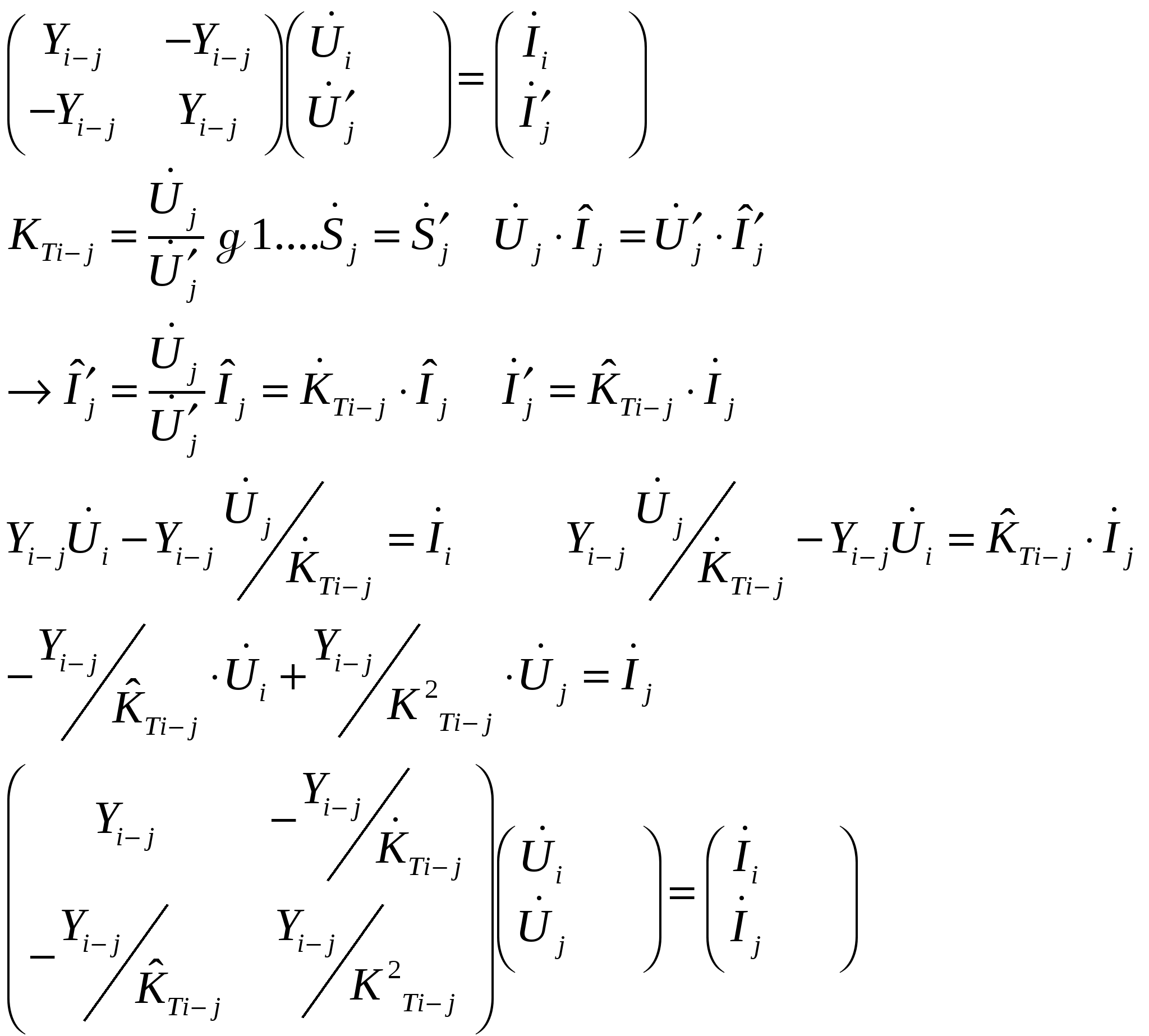

17’ Прямые и итерационные методы решения систем линейных алгебраических уравнений (СЛАУ). Необходимость использования этих методов для решения задач расчета установившихся режимов.
1) прямые (точные) методы – дают решение за конечное число арифметических итераций, которое определяется вычислительной схемой метода а также порядком и структурой матрицы коэффициентов СЛАУ. (Гаусса)

2) Итерационные – это методы, в которых за счет многократного выполнения однообразных вычислений (итераций) получается решение с наперед заданной точностью. Чем выше точность, тем больше количество итераций. (м. Зейделя, min ф-ции ошибки, релаксационные методы)

2ое уравнение (бал. мощностей) – сугубо нелинейное – решается с помощью линеаризации в каждой точке.

Матричные узловые ур-я в форме баланса токов или мощностей – это системы нелинейных уравнений, которые характеризуются как простотой формирования, так и большими возможностями с точки зрения эффективной организации процесса их решения. Нелинейные Ур-я содержат в общем случае n комплексных уравнений с n комплексными неизвестными напряжениями в узлах
В результате получаем СЛАУ, которую необходимо решать на каждой итерации.

18’ Метод Гаусса с обратным ходом. Вычислительная схема пр и обр хода. +/- метода

1 этап: Прямой ход: n шагов – матрица коэффициентов приводится к треугольному виду:

2 этап: Обратный ход – находятся X_n_-1,….X₁

1 этап: , а для для К-го шага:

2 этап:

«+» : 1) прямой (точный) метод, получаем решение за конечное число шагов. 2) если диагональн элементы >> недиагональных, то хорошая точность расчета

«-» : 1)вычисления по формулам (2) и (3) дают большую погрешность, если диагональн элементы → 0 (малы)

2)вычисления по формулам (4) и (5) могут дать большие погрешности, если вычитаются близкие величины (при detA → 0). Неточность задания исходных данных может привести к большой погрешности, ПРИМЕР: сис-ма уравнений 1000x₁+x₂=1002; 2001x₁+2x₂=2005; решая ее получим x₁= 1, x₂= 2. Изменив исх данные с ε=0,1% система будет: 1001x₁+x₂=1002; 2001x₁+2x₂=2005; решив новую систему получим: x₁= -1, x₂= 2003.

3)При выполнении прямого хода метода Гаусса первоначально слабозаполненная матрица коэффициентов, если не принять спец. мер, после 1го шага оказывается полностью заполненной.

19’ Алгоритмическая и программная реализация метода Гаусса с обратным ходом.

Алгоритм:

Прямой ход:

Обратный ход:

Программная реализация:

Subroutine Gauss (A,B,n,l)

Complex A(l,l), B(n)

do k = 1,n-1

b(k) = b(k) / a(k,k)

do j = k+1, n

a(k,j) = a(k,j) / a(k,k)

b(j) = b(j) - a(j,k) ∙ b(k)

do i = k+1, n

a(i,j) = a(i,j) – a(i,k) ∙ a(k,j)

end do

end do end do

! обратный ход

b(n) = b(n) / a(n,n)

do i = n-1, 1, -1

do j = i+1, n

b(i) = b(i) – a(i,j) ∙b

end do

end do

end

1 2 3 4 5 6

20’ Принципы учета слабой заполненности сетевых матриц при использовании метода Гаусса.
1) Порядок исключения ненулевых элементов в методе Гаусса должен быть таким, чтобы в процессе исключения появились минимальное кол-во новых ненулевых элементов;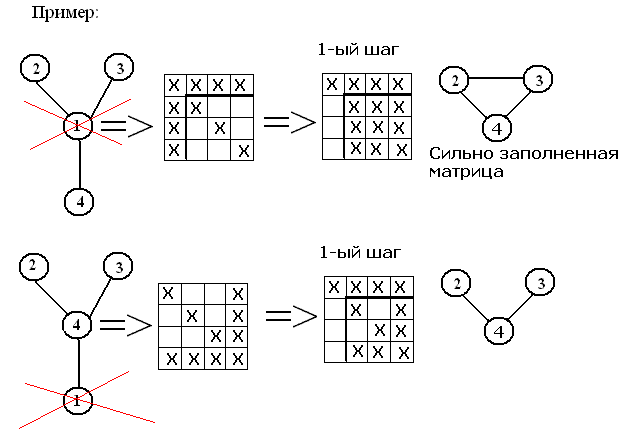

Итог: 1) Надо либо менять порядок следования исходных узлов

2) Либо не изменяя порядка исключения переименовывая узлы (см билет 23)
Порядок исключения: в первую очередь должны исключаться узлы менее всего связанные с другими узлами (имеющие наименьшее число инцидентных связей с другими элементами)
2) Хранить в памяти машины нужно только ненулевые элементы и только с ними нужно производить арифметические операции (см билет 24)

21’ Порядок исключения неизвестных в методе Гаусса с обратным ходом.
1) Порядок исключения ненулевых элементов в методе Гаусса должен быть таким, чтобы в процессе исключения появились минимальное кол-во новых ненулевых элементов;

22’ Коэффициент заполненности матриц. Хранение ненулевых элементов матриц.

- кол-во элементов; n – кол-во узлов; m – ветвей

В больших схемах

Вывод: чем больше кол-во узлов схемы тем меньше коэффициент заполненности
Хранить необходимо только ненулевые элементы матрицы Y, причем только верхний Δ, так как матрица Y – симметрична

(см билет 24)
Требования к схемам хранения матриц.

1) Компактность

2) Простота формирования

3) Простота использования

а) простота выборки элементов

б) гибкость изменения хранимой информации

(т.к. поле 1 шага появл. новые ненул элементы)

I. Задаем только ненул. элементы:

VALUE	Y₁₂	Y₄₃	Y₃₃	Y₂₃	- значения
ILINE	1	4	3	2	- номер строки
ICOL	2	3	3	3	- номер столбца

Экономия от n² до 4n чисел

23’ Алгоритмы упорядочения, их классификация.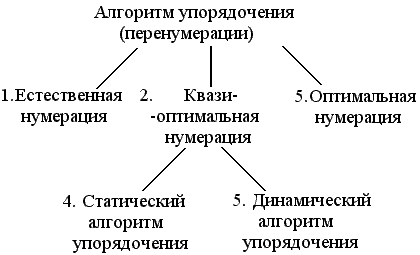

2) компромисс между программно не очень сложной перенумерацией и экономией памяти машины

3) процесс упорядочивания проходит до начала исключения узлов

4) осуществляется на каждом шаге прямого хода

5) нумерация, предполагающая миним. требуемый объем памяти, мин. суммарное кол-во ненулевых элементов
При программной перенумерации происходит только имитация процесса исключения неизвестных

24’ Хранение слабозаполненных матриц. Схемы упаковки матриц. Требования к схемам хранения матриц.

1) Компактность

2) Простота формирования

3) Простота использования

а) простота выборки элементов

б) гибкость изменения хранимой информации

(т.к. поле 1 шага появл. новые ненул элементы)

I. Задаем только ненул. элементы:

VALUE	Y₁₂	Y₄₃	Y₃₃	Y₂₃	- значения
ILINE	1	4	3	2	- номер строки
ICOL	2	3	3	3	- номер столбца

Экономия от n² до 4n чисел

II. Организуем отдельно массив диагональных элементов, для которых не храним номер строки и столбца:

DIAG	Y₁₁	Y₂₂	Y₃₃	“-“ многократное прохождение, чтобы найти номера узлов связанных с данным
VALUE	Y₁₂	Y₄₃	Y₃₃
ILINE	1	4	2
ICOL	2	3	3

III.

VALE	Y₁₂	Y₁₅	Y₂₁	NZERO – количество ненул. элементов, связанных с данным узлом, искл. ILINE
ICOL	2	5	1
DIAG	Y₁₁	Y₂₂	Y₃₃
NZERO	2	2	3

IV.

DIAG	Y₁₁	Y₂₂	Y₃₃	Чтобы не перестраивать весь массив, появл. элементы дописываются в конец, но перекомпилируется массив INEXT
ILINE	1	1	2
ICOL	2	5	1
INEXT	2	2	3
VALUE	Y₁₂	Y₁₅	Y₂₁

25’ Алгоритм формирования матрицы У в компактной форме.

У₁₁	У₁₂	У₁₃		У₁₅
×	У₂₂	У₂₃
×	×	У₃₃	У₃₄	У₃₅
		×	У₄₄
×		×		У₅₅

diag	У₁₁	У₂₂	У₃₃	У₄₄	У₅₅
nzero	3	1	2	0	0

Только те эл-ты, которые есть в верхнем Δ

value	У₁₂	У₁₃	У₁₅	У₂₃	У₃₄	У₃₅
icol	2	3	5	3	4	5
nadr	1	4	5	7	7

Создается доп массив NADR – номер ячейки массива VALUE, с которого начинаются проводимости, связанные с этим узлом
7 – потому что 6 эл-тов всего в VALUE, показывает что больше ни с чем не связано.

26’ Алгоритмическая и программная реализация формирования матрицы Y в компактной форме.См.25 Программа:

Subroutine ysz (nn, nk, z, yc, y, diag, nzero, value, icol, nadr, n, m)

Complex z(m), yc(m), diag(n), value (1)

Dimension nzero(n), icol(1), nadr(n)

do i=1,m

diag(i)=(0.0)

nzero(i)=0

end do; do i=1,m

i1=nn(i)

i2=nk(i)

y(i)=(1,0.)/z(i)

if(i1*i2.ne.0) then j=i2

if (i2.gt.i1) j=i1

nzero(j)= nzero(j)+1

diag(i1)= diag(i1)+y(i)+0.5*yc(i)

else i2=i1+i2

endif

diag(i2)= diag(i2)+y(i)+0.5*yc(i)

end do

nadr(1)=1 do i=2,n

nadr(i)= nadr(i-1)+ nzero(i-1)

end do do i=1,m

i1=nn(i)

i2=nk(i)

if(i1*i2.ne.0) then j=i2

if (i2.gt.i1) j=i1

k=nadr(j)

nadr(j)= nadr(j)+1

value (k)=-y(i)

icol(k)= i1+i2=j

endif

end do end return