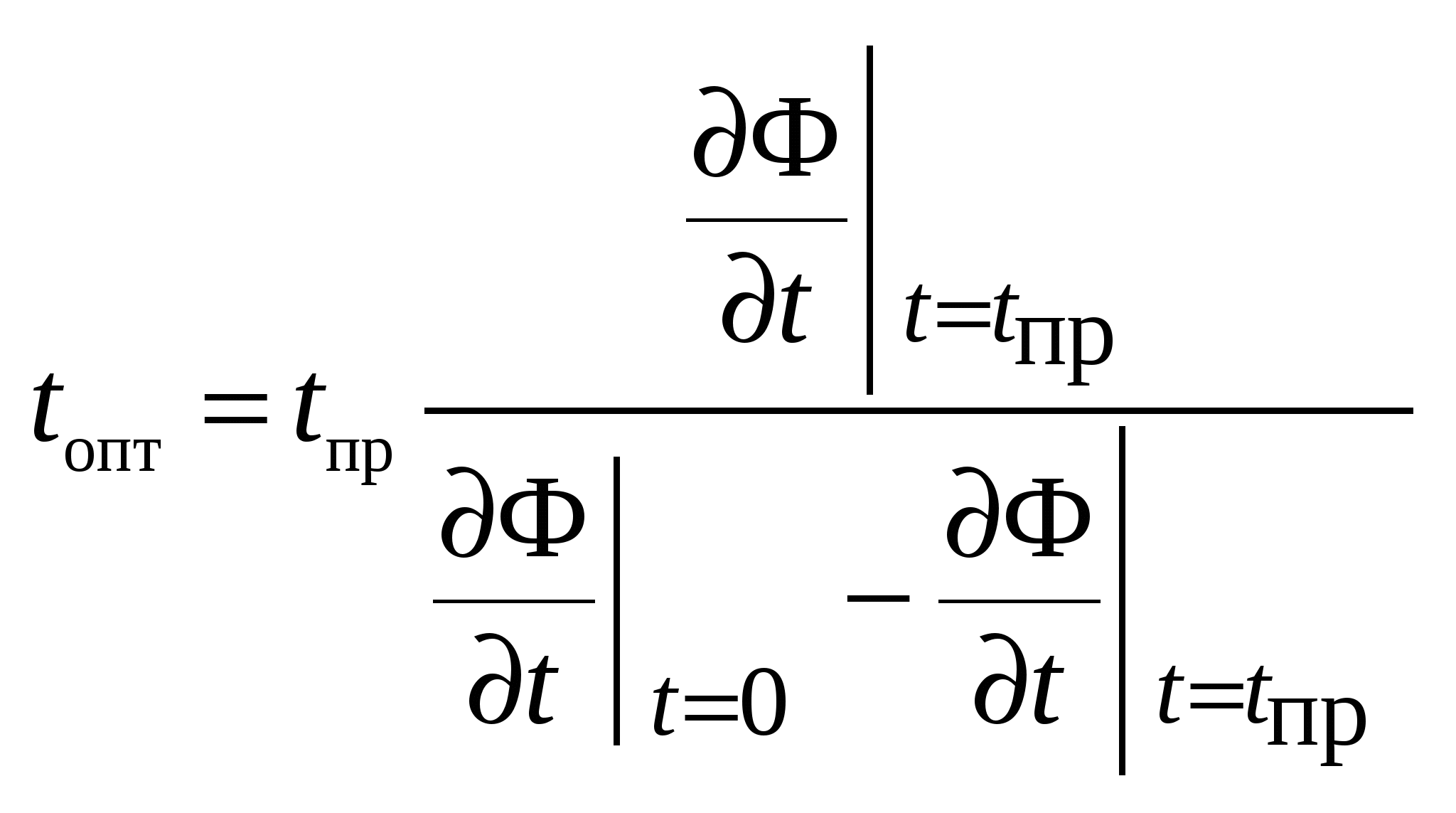70’ Матричное выражение градиента функции Ф(х) в градиентном методе расчёта УР.
В матричной форме:
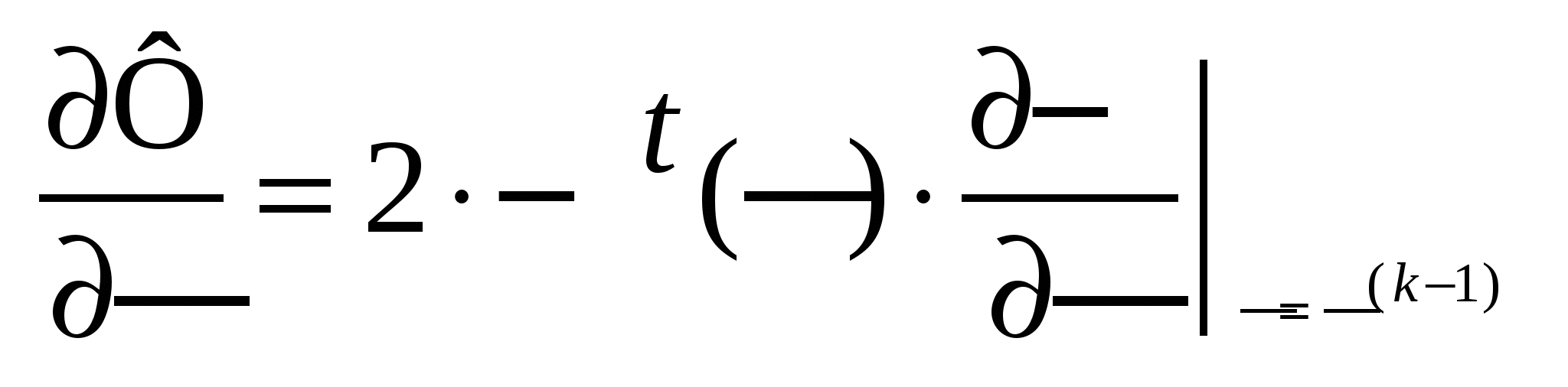
Транспонированный | Матрица Якоби
вектор небаланса |
|
71’ Алгоритм решения системы уравнений УР градиентным методом.
Алгоритм:
Для Х(k) находим 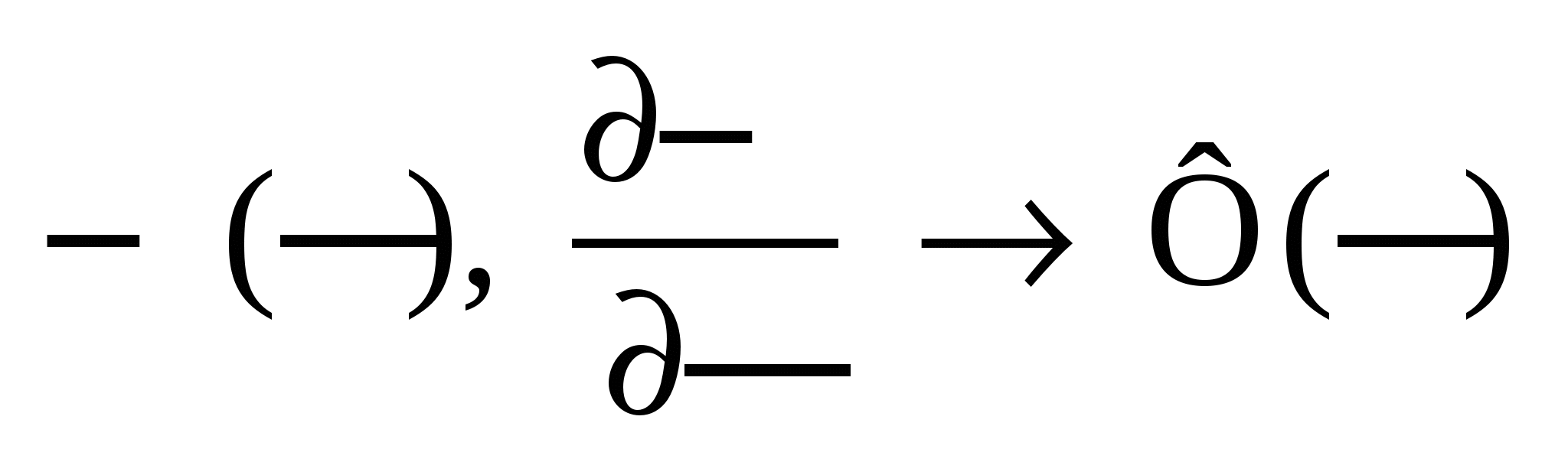
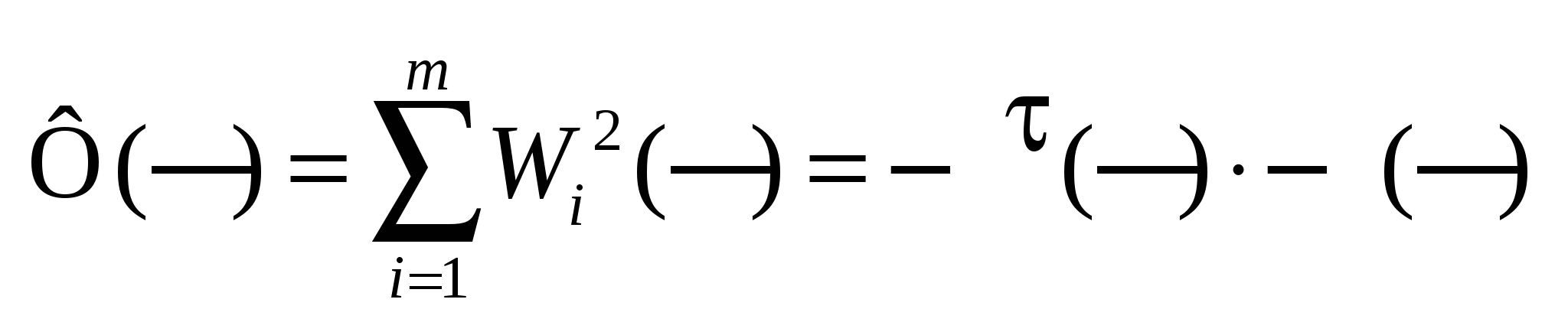
Проверяем: 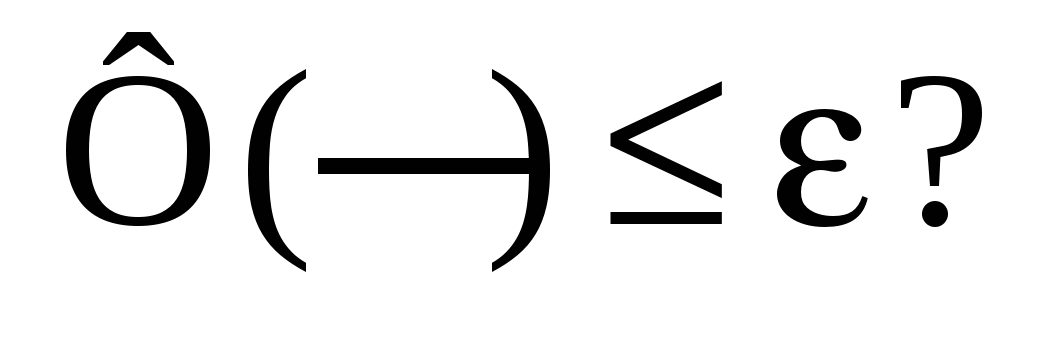
Если да, то расчёт закончен. Или проверяем:
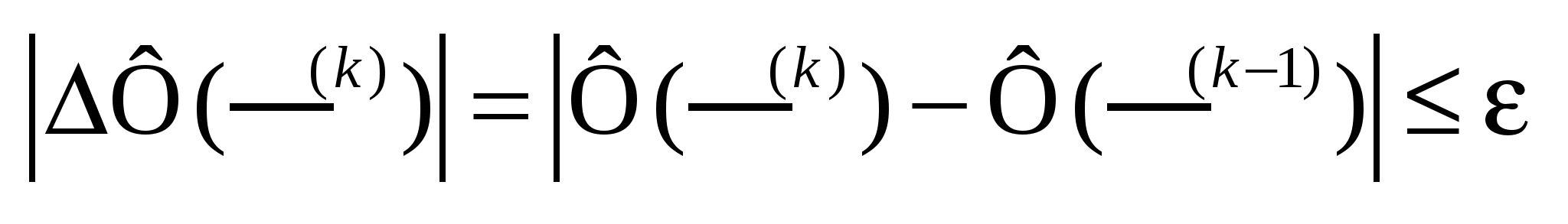
Если п.2 не выполняется, то: 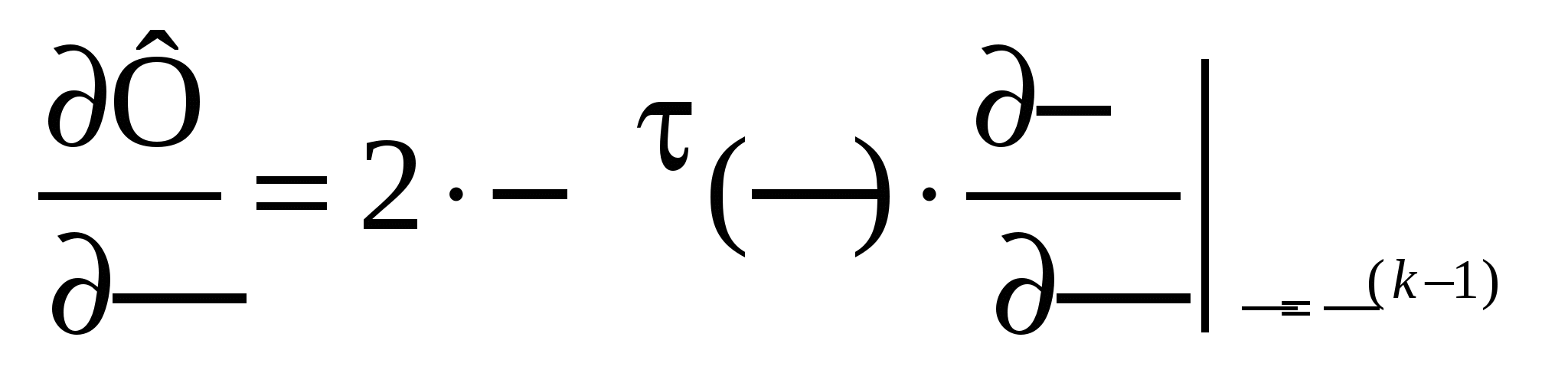
Выбирается шаг t для движения в направлении антиградиента.
Находим следующее приближение переменных:
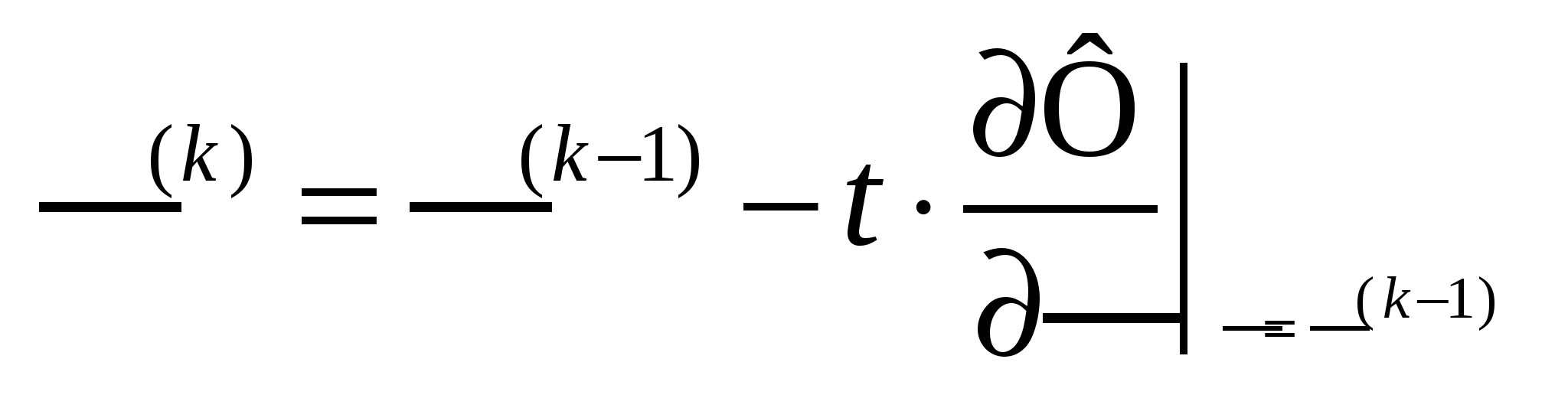
Повторить с п.1
|
72’ Понятие шага t и способы его выбора в градиентном методе расчёта УР.
Шаг t – шаг, который мы делаем в направлении антиградиента
Выбирается эмпирически
Выбирается аналитическими методами
См. билеты 73,74
|
7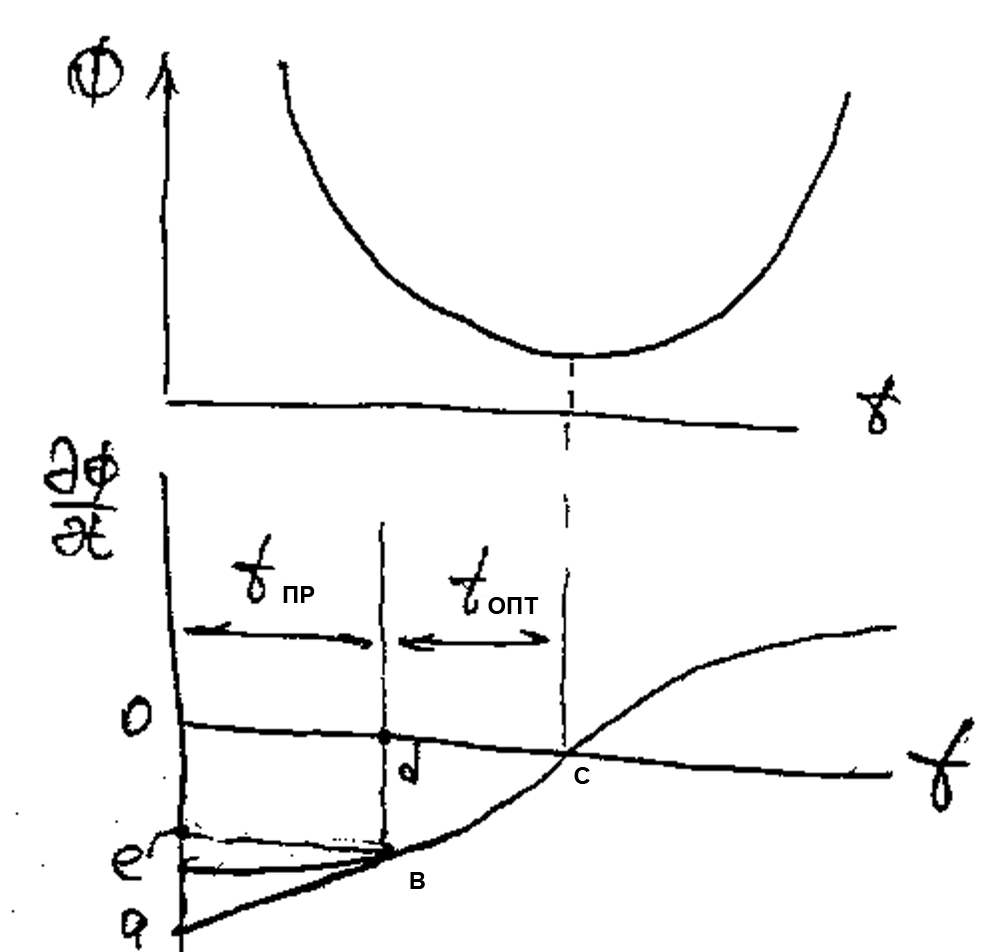 3’/74’ Аналитический способ определения оптимального шага tопт в градиентном методе расчёта УР. 3’/74’ Аналитический способ определения оптимального шага tопт в градиентном методе расчёта УР.
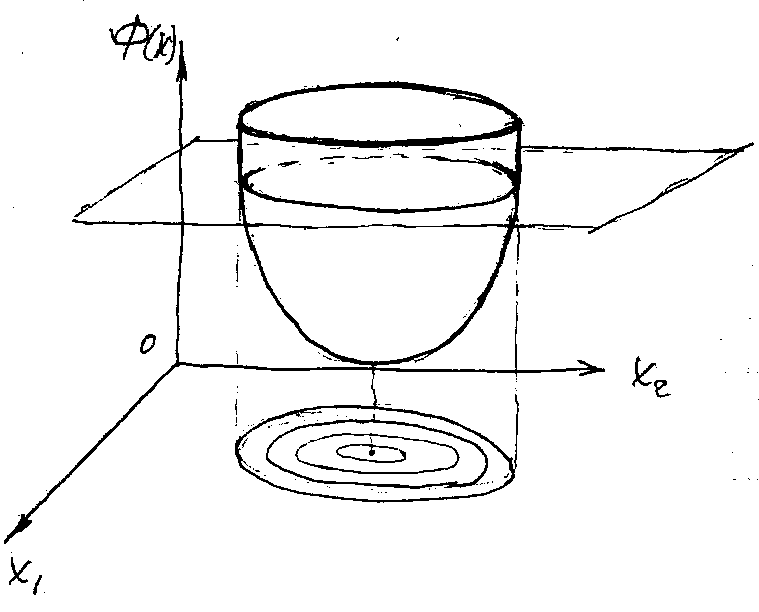
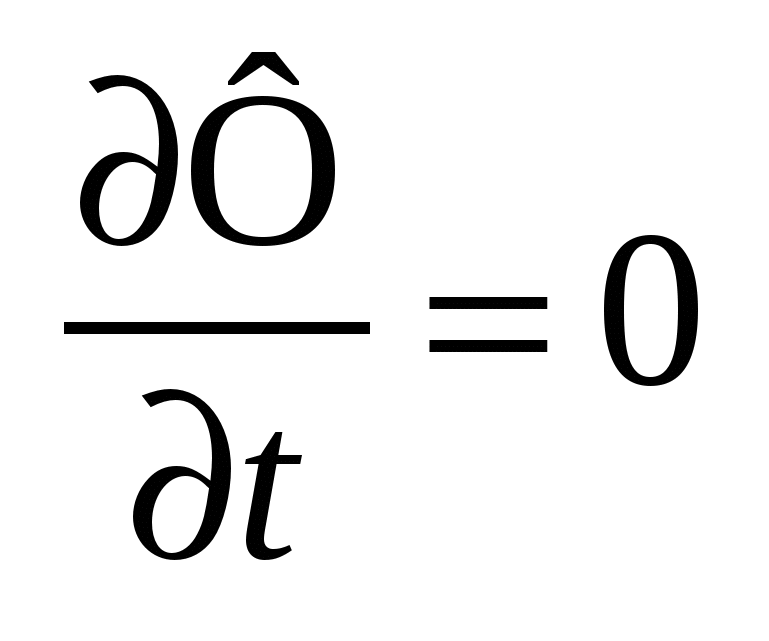 - Ф зависит только от шага. Сначала делаем пробный шаг, а потом подходим к оптимальному - Ф зависит только от шага. Сначала делаем пробный шаг, а потом подходим к оптимальному
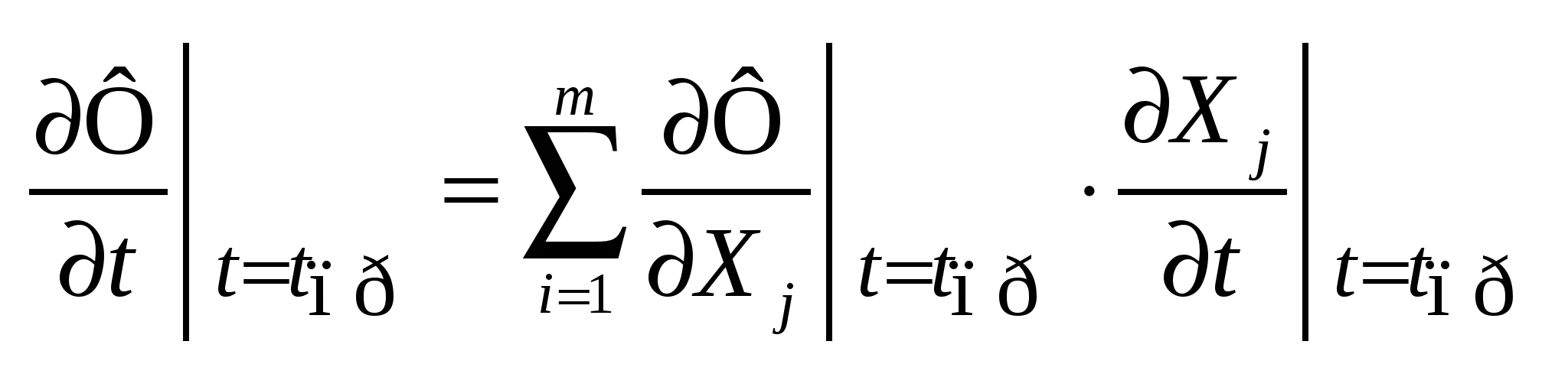 (4) (4)
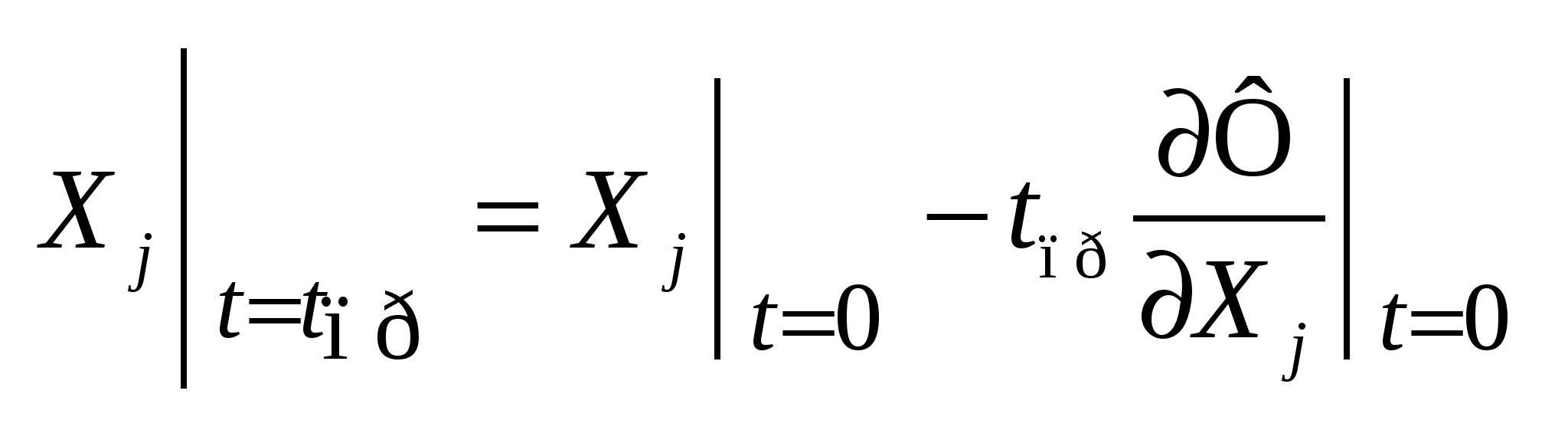
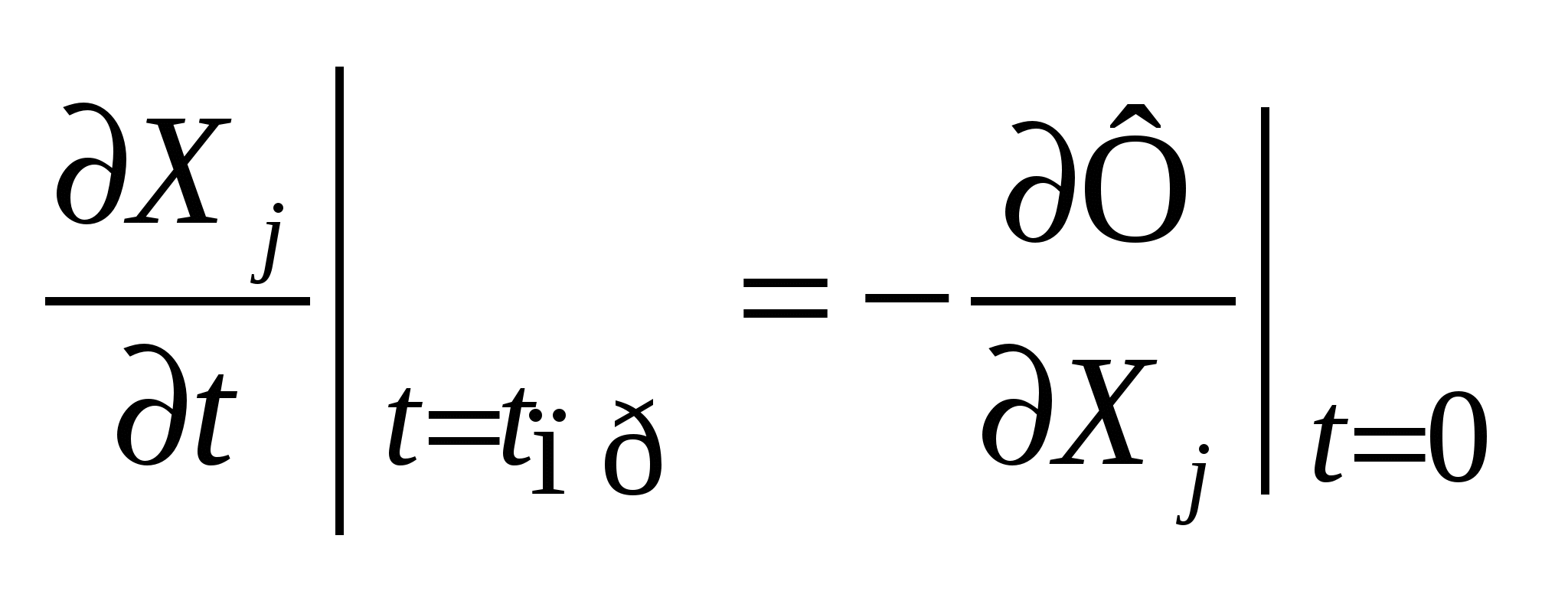 (5) (5)
|
73’/74’ Продолжение.
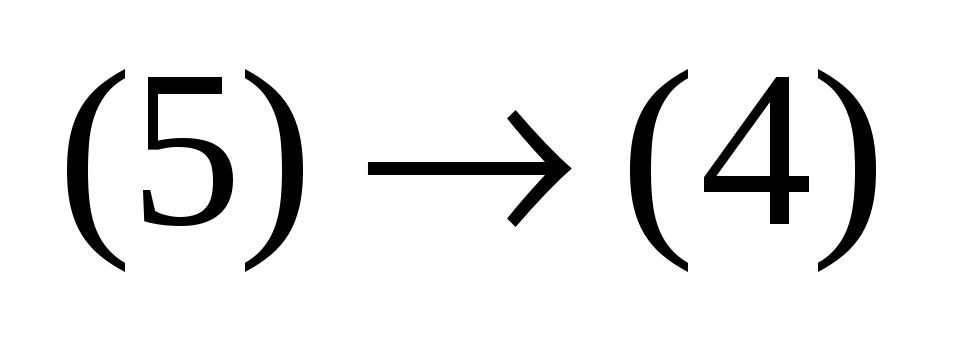 : :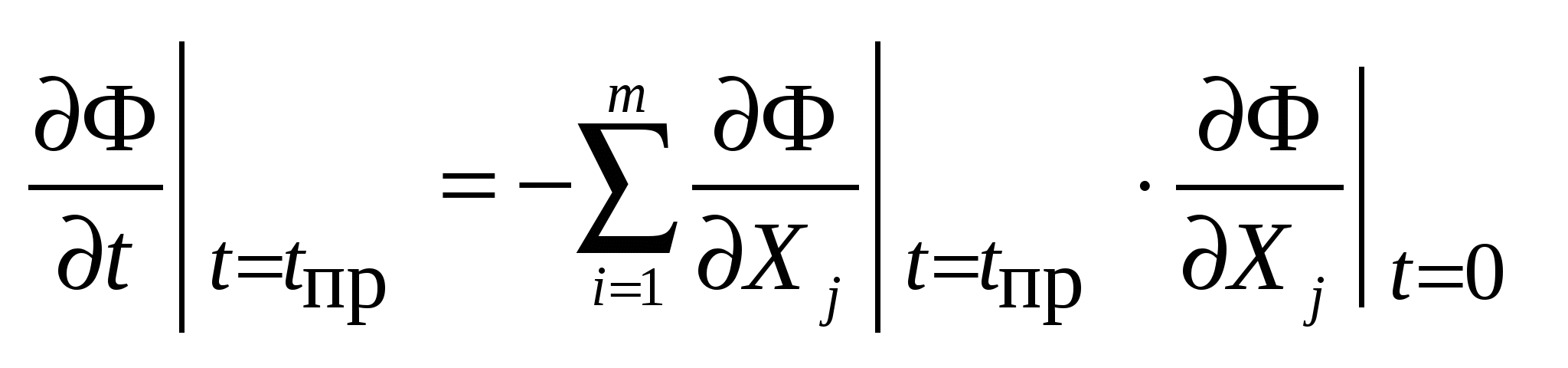
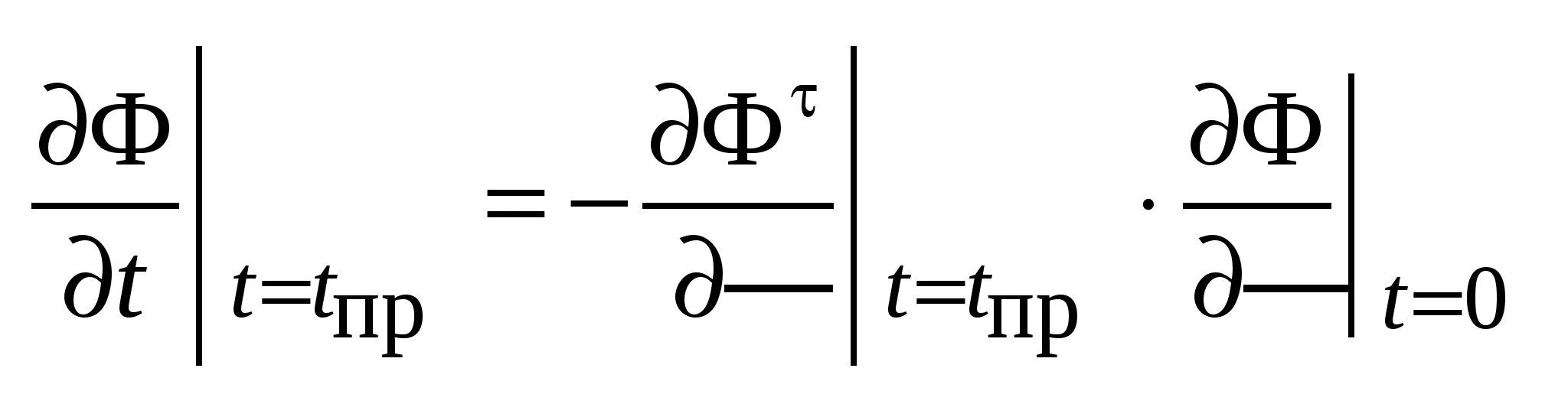
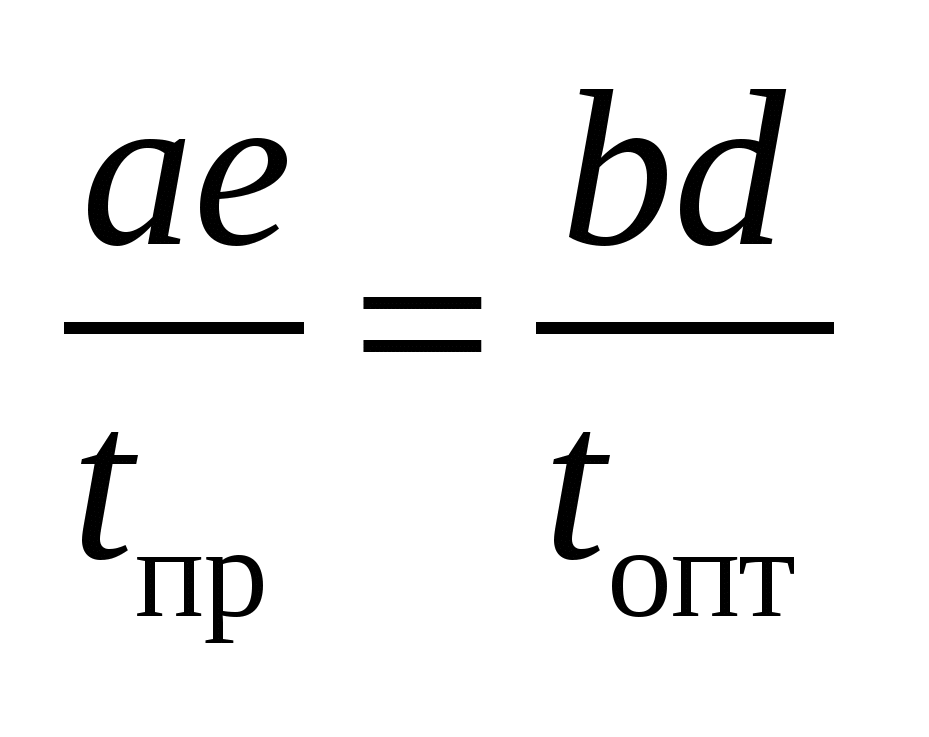 ; ; 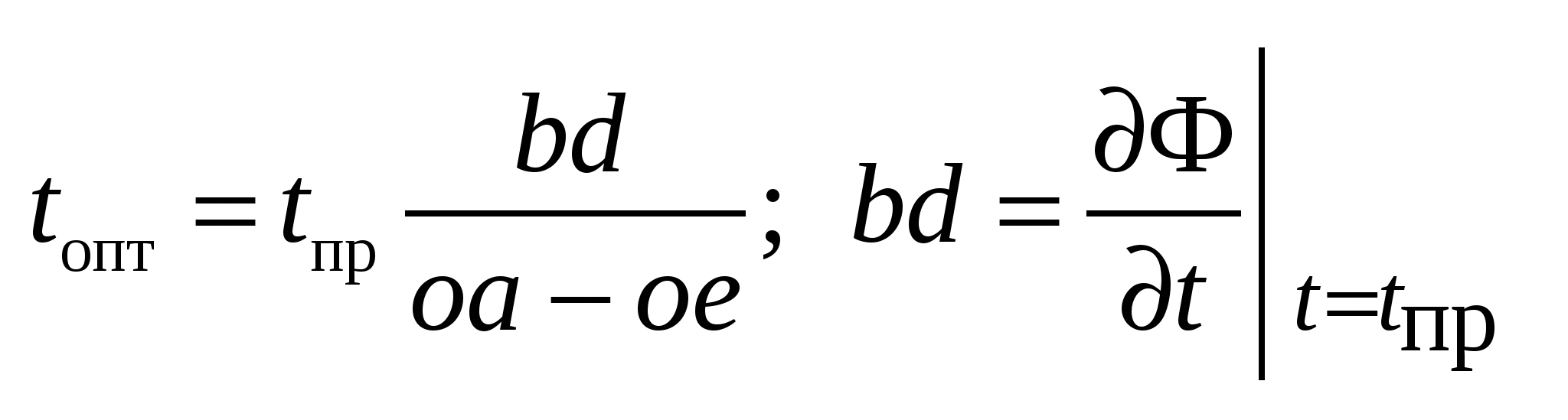
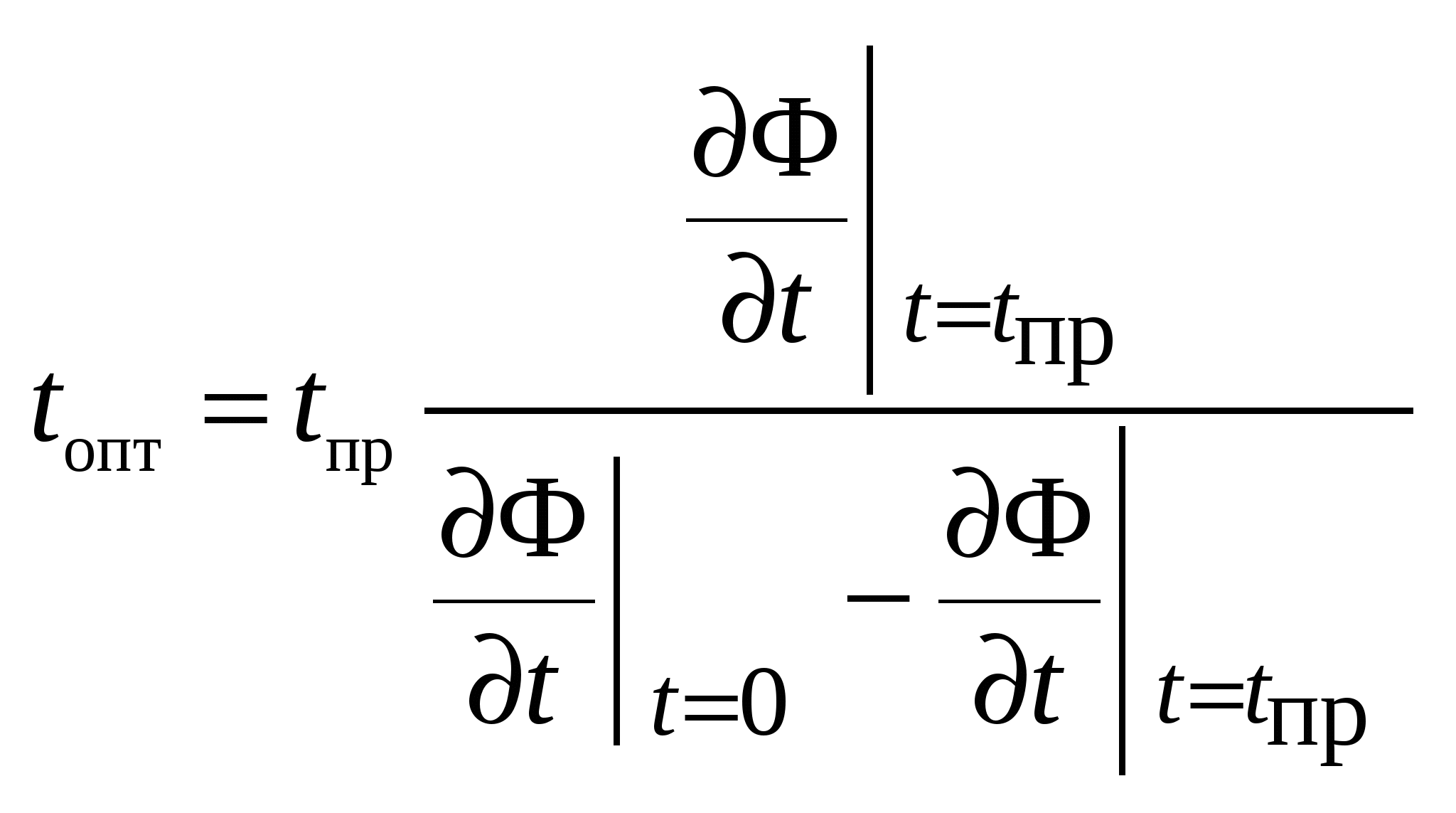
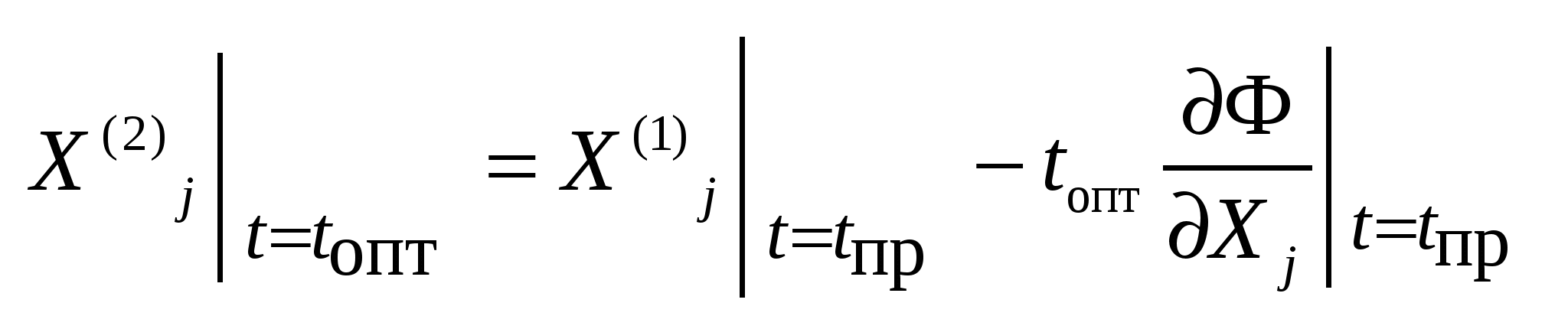
При приближении к min область сходимости метода замедляется- нужно искать свой оптимальный шаг.
Но область сходимости всё равно очень большая.
Для расчёта режимов метод не применяется в силу своей сложности, применяется для оптимизационных задач.
|
1. Области рационального использования средств ВТ. Характеристика каждой из областей. 2. Техническая постановка задачи расчета установившегося режима (УР). Самостоятельное и подчиненное значение расчетов УР. Результаты расчета УР. 3. Классификация элементов ЭЭС (активные, пассивные, узловые, линейные). Модели всех элементов ЭЭС. Классификация узлов. 4. Модель ветви, модель узла. Генераторные, нагрузочные узлы. Базисный узел. 5. Обобщенная статическая характеристика нагрузки по напряжению (СХН).Возможность представления нагрузки различными способами на основе СХН. 6. Представление исходных данных об ЭЭС для расчета УР в ней. 7. Ядро информационно-вычислительной системы. База данных. Модели данных. СУБД и ее функции. 8. Основные уравнения, описывающие установившийся режим ЭЭС. Узловое уравнение состояния ЭЭС (в форме баланса токов, мощности). 9. Базисный и балансирующий узлы. Требования к выбору балансирующего узла. 10. Базисный узел. Необходимость задания базисного узла в расчетах УР. 11(вместе с «9»).Балансирующий узел. Требования к выбору балансирующего узла. 12.Узловое уравнение состояния ЭЭС в форме баланса токов или мощности при условии совмещения базисного и балансирующего узлов. 13.Формирование матрицы узловых проводимостей. Алгоритм и программная реализация.
14.Алгоритмическая и программная реализация формирования матрицы узловых проводимостей Y. 15. Учет трансформаторных связей в схеме замещения электрической сети. 16.Учет трансформаторных ветвей при формировании матрицы узловых проводимостей Y. 17.Прямые и итерационные методы решения систем линейных алгебраических уравнений (СЛАУ). Необходимость использования этих методов для решения задач расчета установившихся режимов.
----МЕТОД ГАУССА-и –ХРАНЕНИЕ МАТРИЦ--18.Метод Гаусса с обратным ходом. Вычислительная схема прямого и обратного хода. Преимущества, недостатки метода. 19. Алгоритмическая и программная реализация метода Гаусса с обратным ходом. 20. Принципы учета слабой заполненности сетевых матриц при использовании метода Гаусса. 21.Порядок исключения неизвестных в методе Гаусса с обратным ходом. 22. Коэффициент заполненности матриц. Хранение ненулевых элементов матриц. 23. Алгоритмы упорядочения, их классификация. 24. Хранение слабозаполненных матриц. Схемы упаковки матриц. Требования к схемам хранения матриц. 25. Алгоритм формирования матрицы Y в компактной форме. 26.Алгоритмическая и программная реализация формирования матрицы Y в компактной форме. ---МЕТОД ЗЕЙДЕЛЯ-----27.Итерационные методы расчета установившихся режимов (поузловые, одновременного решения уравнений). Области сходимости, вычислительная эффективность. Алгоритм расчета УР методом Зейделя. 28. Метод Зейделя применительно к решению нелиней ного узлового уравнения в форме баланса токов. 29. Алгоритмическая и программная реализация метода Зейделя. З0. Свойства метода Зейделя, используемого для расчета установившихся режимов сложных ЭЭС. Коэффициент ускорения.
|
31.Достаточные условия сходимости метода Зейделя применительно к решению нелинейного узлового уравнения в форме баланса токов. 32.Вычислительная схема метода Зейделя при задании генераторных узлов в форме Pг, Uг. ----РАЗЛ.МЕТОДЫ-ДЛЯ-БАЛ-ТОКОВ----33.Решение нелинейного узлового уравнения в форме баланса токов на основе метода Гаусса. Блок-схема алгоритма расчета установившегося режима. 34.Решение нелинейного узлового уравнения в форме баланса токов на основе обращения матрицы Y. Блок-схема алгоритма расчета установившегося режима. 35.Решение нелинейного узлового уравнения в форме баланса токов на основе L-H факторизации матрицы Y. Блок-схема алгоритма расчета установившегося режима. З6. Решение уравнений установившегося режима на основе L-H факторизации матрицы коэффициентов. Вычислительная схема прямой и обратной подстановки. 37. L-H факторизация матрицы коэффициентов системы линейных алгебраических уравнений (матрицы А). Алгоритм вычисления элементов факторизованной матрицы. 38. Алгоритмическая и программная реализация L-H факторизации матрицыА. 39.Методы, используемые для расчета УР при записи узловых уравнений в форме баланса токов. 40.Методы расчета режимов, основанные на сочетании методов Зейделя и Гаусса. Достоинства и недостатки. 41.(вместе с «39»)Методы, применяемые для решения комплексного узлового уравнения в форме баланса токов.
–НЬЮТОН-ПРЯМ-и-ПОЛЯРН-СИСМЫ-КООРД---- 42.Методы расчета установившегося режима, требующие разделения узлового уравнения в комплексной форме на два уравнения с действительными коэффициентами. Прямоугольная и полярная системы координат.
43.Узловое уравнение состояния электрической системы в форме баланса мощности, записанное в прямоугольной системе координат. 44.Узловое уравнение состояния электрической системы в форме баланса мощности при записи напряжений в полярной, а проводимостей - в прямоугольной системах координат. 45.Узловое уравнение состояния электрической системы в форме баланса мощности, записанное в полярной системе координат. 46.Возможные формы записи нелинейных узловых уравнений установившегося режима для решения их методами, требующими разделения комплексных I ременных на действительные составляющие. 47.Метод Ньютона решение узлового уравнения методом Ньютона, записанного в прямоугольной и полярной системе координат. 48.Зависимость размерности системы уравнений установившегося режима от формы записи и формы представления генераторных узлов. 49.3ависимость размерности матрицы Якоби от формы представления генераторных узлов и системы координат, в которой записаны узловые уравнения в форме баланса мощности. 50.Аналитическое выражение элементов матрицы Якоби узловых уравнений в форме баланса мощности, записанных в полярной системе координат. 51.Свойства матрицы Якоби. Свойства метода Ньютона. 52.Модификации метода Ньютона. 53.Модифицированный метод Ньютона. Сущность и область сходимости.
54. Метод Ньютона по параметру. Сущность и область метода.
|
55.Способы определения параметра t в методе Ньютона по параметру. 56.Метод Ньютона с разделением переменных (блочная диагонализация матрицы Якоби). Сущность и область сходимости метода. 57.Модификации метода Ньютона, сокращающие объем вычислений на каждой итерации. Скорость и область сходимости этих методов.
58.Методы расчета установившихся режимов сложных ЭЭС, их сопоставление. 59.Использование метода Гаусса, обращения или L-H факторизации матрицы коэффициентов системы линейных алгебраических уравнений в расчетах режимов методом Ньютона. 60.Возможные методы решения системы линейных алгебраических уравнений (СЛАУ) в расчетах установившихся режимов методом Ньютона.
------ПК--------------61.Характеристика современных программно-вычислительных комплексов (ПВК), содержащих расчет установившихся режимов. 62.Основные задачи, решаемые на основе использования ПВК РАСТР. 6З.ПВК ДАКАР. 64. ПВК МУСТАНГ. 65. ПВК EUROSTAG. 66 ПВК КОСМОС . ------ГРАДИЕНТ---- 67 Градиентный метод расчета уравнений УР. Сущность, область сходимости. 68. Система уравнений, характеризующая необходимое условие минимума функции Ф(х) в градиентном методе расчета УР. 69. Понятие градиента, антиградиента функции Ф(х). Математическая формулировка итерационного процесса градиентного метода расчета УР. 70. Матричное выражение градиента функции Ф(х) в градиентном методе расчета УР. 71. Алгоритм решения системы уравнений УР градиентным методом. 72. Понятие шага t и способы его выбора в градиентном методе расчета УР. 73. Аналитический способ определения оптимального шага tonт в градиентном методе расчета УР. 74. Понятия пробного (tпр) и оптимального (tопт) шагов в градиентном методе расчета УР. Аналитическое выражение оптимального шага tопт.
|
 Скачать 2.65 Mb.
Скачать 2.65 Mb.
 3’/74’ Аналитический способ определения оптимального шага tопт в градиентном методе расчёта УР.
3’/74’ Аналитический способ определения оптимального шага tопт в градиентном методе расчёта УР.