|
|
Высшая математика. Вышка. 1. Определители и их свойства
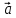 = =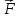 – постоянная сила – постоянная сила
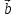 = =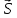 – вектор перемещения – вектор перемещения
|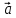 · ·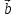 |= | |= |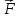 · ·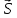 | =A – работа силы | =A – работа силы 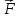 на перемещении на перемещении 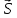 Свойства: 
Векторным произведением двух векторов а и b наз. вектор С, удовлетворяющий условиям: 1.|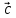 |=| |=|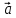 || ||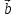 |sin |sin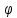 2.Вектор С перпендикуляен вектором а и b 3.Вектора a,b,c образуют правую тройку, т.е из конца третьего вектора C кратчайший поворот от вектора а ко второму вектору b виден против часовой стрелки. 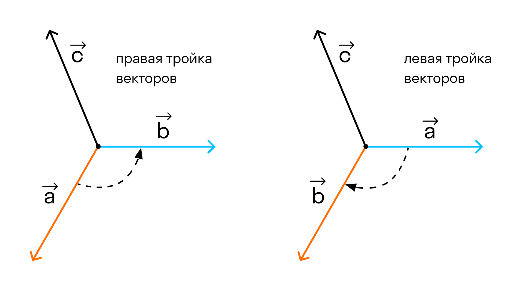
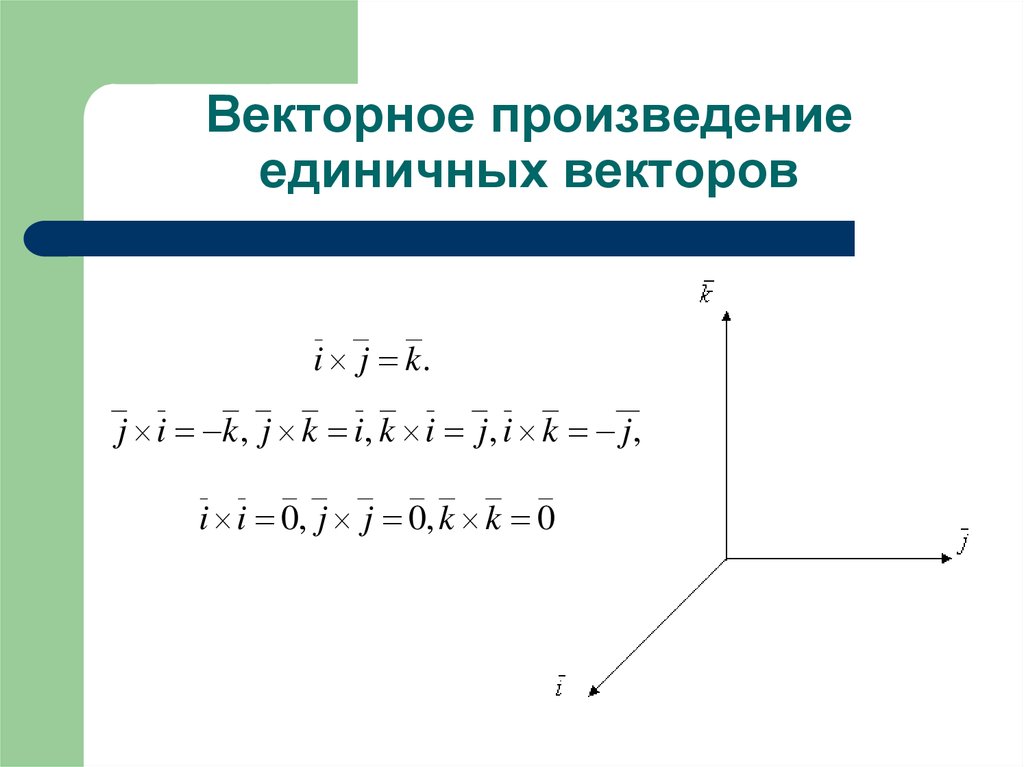
Свойства: jxk=i
9. Смешанное произведение векторов, его свойства.
Определение: Смешанным произведением некомпланарных векторов , наз. объём параллелепипеда, построенного на данных векторах
Свойства:
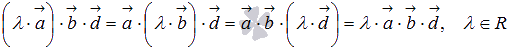 ; ;
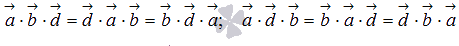
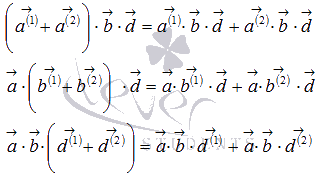
10. Функция. Предел функции в точке и его геометрический смысл.
Функцией наз. закон или правило, согласно которому каждому элементу х Є х становится в соответствие единственный элемент y Є Y при этом пишут
y=f(x)
Cпособы задания функции:
Аналитический
Графический
Табличный
Аналитический способ
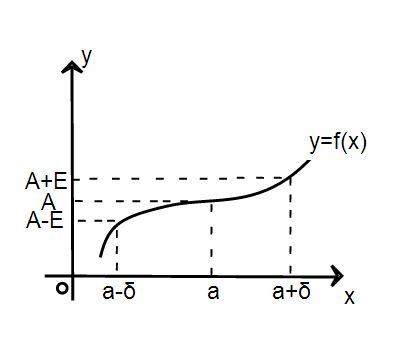
Предел функции в точке существует и равен , если для любой -окрестности точки можно указать такую -окрестность точки , что для любого из этой -окрестности значение будет находится в -окрестности точки . Отметим, что по определению предела функции в точке для существования предела при не важно, какое значение принимает функция в самой точке . Можно привести примеры, когда функция не определена при или принимает значение, отличное от . Тем не менее, предел может быть равен .
11. Теоремы о пределах
1) Если функция имеет предел при хх0 то в некоторой окрестности U(x0) она представляется в виде суммы А+а(х) где А-ее предел, а а(х)- б.м.в. при хх0. Верно и обратное.
2) Предел суммы конечного числа функций равен сумме пределов этих функций:
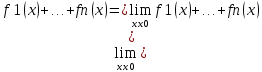 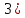 Предел произведения конечного числа функций равен произведению пределов этих функций: Предел произведения конечного числа функций равен произведению пределов этих функций:
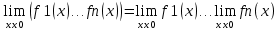
Если С=const 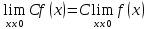
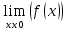 n = ( n = (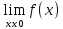 )n )n
4) Если 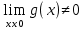 , то , то 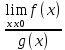 = = 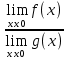
5) Если в некоторой окресности U(x0) выполняется f1(x) ≤ g(x) ≤ f2(x) и 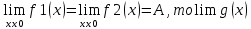 =A =A
|
|
|
 Скачать 242.71 Kb.
Скачать 242.71 Kb.