Высшая математика. Вышка. 1. Определители и их свойства

• Название: 1. Определители и их свойства
• Анкор: Высшая математика
• Дата: 26.01.2022
• Размер: 242.71 Kb.
• Имя файла: Вышка.docx
• Тип: Документы; #342730
• страница: 3 из 4

12. Первый и второй замечательный пределы
Формула первого замечательного предела

Следствия первого замечательного пределазапишем формулами
1.
2.
3.
4.

Второй замечательный предел равен экспоненте

Это классика к которой в реальных задачах на пределы не всегда легко прийти.
В вычислениях Вам понадобятся пределы - следствия второго замечательного предела:
1. 2.

3. 4.
Благодаря второму замечательному пределу и его последствиям можно исследовать неопределенности типа ноль разделить на ноль, единица в степени бесконечность, и бесконечность разделить на бесконечность, да еще и в таком же степени


13. Бесконечно большие и бесконечно малые величины (б. м. в.). Сравнение б. м. в. Эквивалентные б. м. в.
Бесконечно малая — числовая функция или последовательность, стремящаяся к (пределу которой
равен) нулю. = 0

Бесконечно большая — числовая функция или последовательность, стремящаяся к (предел которой равен) бесконечности определённого знака.

. = 



Если этот предел представляет собой конечное ненулевое число, то     и     называются бесконечно малыми одного и того же порядка.
Особый интерес представляет частный случай, когда  λ = 1. Тогда говорят, что     и    являются эквивалентными бесконечно малыми при   и записывают это утверждение в виде

      Если  λ = 0, то говорят, что     является бесконечно малой более высокого порядка по сравнению с     при    а функция     имеет меньший порядок малости.

Пусть  x → 0. Тогда справедливы следующие соотношения эквивалентности бесконечно малых функций.


14. Непрерывность функции. Теоремы о непрерывных функциях.
1) Функция f(x) наз. непрерывной в точке x0, если она определена в точке х0 и в некоторой ее окрестности и

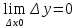
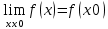
2) Функция f(x) наз. Непрерывной в точке x0, если она определена в этой точке и некоторой ее окрестности, имеет предел при xx0 и этот предел равен значению функции в этой точке
3) Функция f(x), непрерывная во всех точках некоторого промежутка наз. непрерывной на этом промежутке

Теорема 1
Сумма конечного числа непрерывных функций явл. Непрерывной функцией.
Пусть функции f1(x), f2(x)…fn(x) непрерывны в точке x0 и g(x)= f1(x)+f2(x)+…+fn(x) 
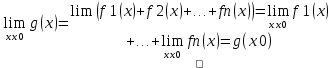
Теорема 2
Произведение конечного числа непрерывных функций является непрерывной функцией
Теорема 3
Частное двух непрерывных функций является непрерывной функцией, если знаменатель в рассматриваемой точке не равен нулю.
Теорема 4
Пусть функция f(U) непрерывна в точке x0 и пусть U(x0)=U0. Тогда сложная функция F(x)=f(U(x)) непрерывна в точке x0.
Теорема 5
Все элементарные функции непрерывны в своей области определения.

15. Точки разрыва функции и их классификация
Если в точке х0 нарушается условие непрерывности функции f(x), то функция наз. Разрывной в точке х0, а точка х0 – точкой разрыва.
Точка х0 наз. Точкой разрыва 1 рода, если существуют конечные односторонние пределы функции, не равные между собой, т.е f(x0-0) ≠ f(x0+0)
Точка х0 наз. точкой устранимого разрыва, если f(x0-0)=f(x0+0)≠f(x0)
Точка x0 называется точкой разрыва 2 рода, если хотя бы один из односторонних пределов не существует или равен бесконечности.

16. Свойства функций непрерывных на отрезке.
Если f(x) непрерывна на [a;b], то она ограничена на [a;b]

Если f(x) непрерывна на [a;b], то на [a;b] сущетсвуют ее наибольшее и наименьшее значения (min, max)

Если f(x) непрерывна на [a;b] и принимает на концах отрезка не равные значения, то для любого промежуточного значения M между этими числами существует по крайней мере одна точка C ϵ (a;b), для которой f(c) =M

17. Производная функции, её геометрический смысл. Производная основных элементарных функций. Правила дифференцирования. Производная сложной функции. Производная неявной функции. Производная функции, заданной параметрическими уравнениями.
Производной от функции f(x) в точке x наз. Предел отношения ее приращения 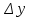в этой точке к соответсвующему приращению аргумента 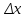при 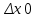и обозначается
f’(x)= =
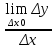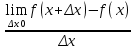
Геометрический смысл производной. Производная в точке x₀ равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.
Производная основных элементарных функций:
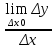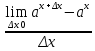y=a^x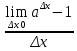
= = a^x = a^x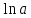

y=sinx
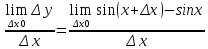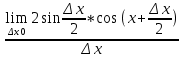= = c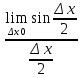osx =cosx

Правила дифференцирования.
1) Если С=const, то (C)’=0
2) (U+-V)’=U’+-V’
3) (UV)’= U’V+V’U
4) ( )’=

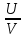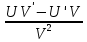
Производная сложной функции
Если функция U=U(x) имеет в точке х производную U’x, а функция y=y(U) в соответсвующей точке U также имеет производную y’u, то сложная функция y=y(U(x)) в точке х имеет производную, равную:
y’x=y’u*U’x
Пример:
y=(x²+3)⁵ y’=5(x²+3)⁴*(x²+3)’=5(x²+3)⁴ * 2x
Производная неявной функции
Во многих задачах, однако, функция может быть задана неявным образом, т.е. в виде уравнения F(x,y)=0.
Для этого, зная уравнение F(x,y)=0, достаточно выполнить следующие действия:

1)Сначала необходимо продифференцировать обе части уравнения по переменной x, предполагая, что y − это дифференцируемая функция x и используя правило вычисления производной от сложной функции. При этом производная нуля (в правой части) также будет равна нулю.
Замечание: Если правая часть отлична от нуля, т.е. неявное уравнение имеет вид f(x,y)=g(x,y),то дифференцируем левую и правую части уравнения.
2)Решить полученное уравнение относительно производной y′(x)

Производная функции, заданной параметрическими уравнениями
Зависимость между аргументом x и функцией y может быть задана в параметрическом виде с помощью двух уравнений x=x(t) ; y=y(t),где переменная t называется параметром.

Пример: x=t² , y=t³ Находим производные x и y по параметру t:

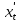=(t²)^’=2t, 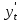=(t³)^’=3t²
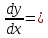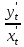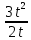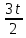Следовательно, y^’_x= = = (t≠0)

18. Производные высших порядков.
Производными высшего порядка наз. Производные второго и более порядка.
Такие производные находятся последовательным дифференцированием данной функции
f’’(x) =
19. Дифференциал функции.
Дифференциалом функции в некоторой точке x называется главная, линейная часть приращения функции.
Дифференциал функции y = f(x) равен произведению её производной на приращение независимой переменной x (аргумента).
Это записывается так:


y=5x⁴ +
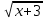
y’= (20x³ + 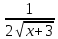* 1)
dy= (20x³ + 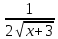)*dx
Геометрический смысл дифференциала. Дифференциал функции y = f(x) равен приращению ординаты касательной S, проведённой к графику этой функции в точке M(x; y), при изменении x (аргумента) на величину 
20. Основные теоремы дифференциального исчисления: Ферма, Ролля, Лагранжа.

Теорема Ферма. (О равенстве нулю производной)

Пусть функция y=f(x) удовлетворяет следующим условиям:

1. 
   она дифференцируема на интервале (a;b);
   
2. 
   достигает наибольшего или наименьшего значения в точке x0∈(a;b).
   

Тогда производная в этой точке равна нулю, то есть f′(x0)=0.

Теорема Ролля. (О нуле производной функции, принимающей на концах отрезка равные значения)

Пусть функция y=f(x)

1. 
   непрерывна на отрезке [a;b];
   
2. 
   дифференцируема на интервале (a;b);
   
3. 
   на концах отрезка [a;b] принимает равные значения f(a)=f(b).
   

Тогда на интервале (a;b) найдется, по крайней мере, одна точка x0 , в которой f′(x0)=0.
Следствие. (Геометрический смысл теоремы Ролля)

Найдется хотя бы одна точка, в которой касательная к графику функции будет параллельна оси абсцисс

Теорема Лагранжа. (О конечных приращениях)

Пусть функция y=f(x)

1. 
   непрерывна на отрезке [a;b];
   
2. 
   дифференцируема на интервале (a;b).
   

Тогда на интервале (a;b) найдется по крайней мере одна точка x0 , такая, что f’(c)=

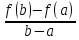
21. Правило Лопиталя.

Если существует предел 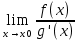то существует 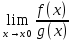причем 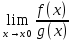= lim(x→x₀)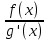

В случае других неопределенностей, с помощью тождественных преобразований необходимо привести выражение стоящее под знаком предела к неопределенност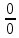и или 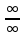; Правило можно применить несколько раз подряд.Пример: (найти пределы)

= =

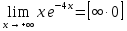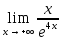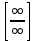
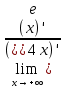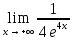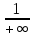= = = =0

22. Исследование функций: интервалы монотонности функции, экстремум функции, необходимое и достаточное условия экстремума функции, интервалы выпуклости графика функции, точки перегиба, асимптоты. Монотонность Если дифференцируемая на отрезке функции f(х) возрастает (убывает), то для любого х(a; b) выполняется условие f '(х) > 0 (f '(х) < 0). (обратное тоже верно)

В некоторых точках мб f '(х)=0 т.к. производная явл. пределом

Экстремум Точка х0 называется точкой локального максимума (минимума) функции f(x), если существует такая окрестность точки х0, что для всех х из этой окрестности выполняется неравенство f (х)  f (х0) (f (х) ≥ f (х0)).

Точки максимума и минимума функции наз. точками локального экстремума. Значения функции в этих точках называются экстремумами функции.

Если функция дифференц. и имеет экстремум в точке Х0, то в этой точке f '(х0) = 0

Необходимое условие экстремума. Если непрерывная функция f(х) имеет в точке х0 экстремум, то в этой точке производная функции равна нулю (f '(х0) = 0) или не существует
Точки, в которых производная функции равна нулю, называются стационарными. Стационарные точки и точки, в которых не существует производная, называются критическими точками функции.

Достаточные условие экстремума. 1)Если производная функции при переходе через точку слева направо меняет знак, то х0 – точка локального экстремума. Если знак производной меняется с „+” на „–”, то х0 – точка max, если „–” на „+”, то х0 – точка min.

2) Пусть х0 – стационарная точка дважды непрерывно дифференц. в этой точке и некоторой ее окрестности функции f(х). Тогда, если f ''(х0)0, то х0 – точка локального min, если

f ''(х0)>0, то х0 – точка локального max.

Интервалы выпуклости графика функции Функция f(х) называется выпуклой (вогнутой) в интервале (a; b), если график этой функции при х(a; b) расположен ниже (выше) касательной, проведенной в произвольной точке из этого интервала.

Точки перегиба Точки, которые отделяют интервалы выпуклости функции от интервалов вогнутости, наз. точками перегиба.

Необходимое условие точки перегиба. Если х0 – точка перегиба функции f (х), то f '' (х0) = 0 или f '' (х0) не существует. Достаточное условие точки перегиба. Пусть функция f (х) определена в точке х0 и некоторой ее окрестности. Если вторая производная f '' (х) функции меняет знак при переходе через эту точку, то х0 – точка перегиба функции.

Асимптоты – прямая наз. асимптотами линией f (х), если расстояние от текущей точки М(находящейся на функции) до этой прямой М стремящаяся к , стремится к 0.

1)Прямая х=а явл. вертикальной асимптотой если пределы 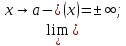f(a-0)

2) 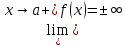; f(a+0)
Если для линии y=f(x) прямая

y=kx+ b – асимптота при х (- )

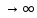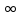k= 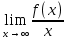; b=f(x)-kx верно и обратное

23. Функции нескольких переменных. Основные определения

Функцией двух переменных наз. закон, по которому каждой паре значений независимых переменных x,y (аргументов) из области определения соответствует значение зависимой переменной z (функции). Областью определения функции двух переменных наз. множество всех пар , для которых существует значение. Найти область определения функции z=

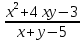
Решение: так как знаменатель не может обращаться в ноль, то: x+y-5≠0 ; y≠5-x

24. Предел функции двух переменных. Примеры.

Число А называется пределом функции f(х. у) при х—›х0,

у—›у0‚ если для любого положительного числа с найдется такая 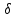—окрестность

точки М0 (x0, у0), что для любой точки М (х‚у) из этой окрестности (за исключением, быть может, самой точки М0), выполняется неравенство |f(x,y)-A| < Σ,

Лишь только |x- х0| < δ, |у-у0| < δ. Обозначают предел функции так

lim f(x,y) = A; х х0; у у0

Пример: z= 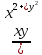для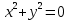

определенную во всей плоскости, кроме начальной точки, и положить дополнительно (0,0) = 0, то получим пример разрыва именно в начальной точке, так как при х→ 0, y→ 0 для функции предела не существует. Однако, рассмотренная функция хоть и не является непрерывной по обеим переменным сразу, но будет непрерывной в этой точке как по х, так и по y в отдельности. Это следует из того, что z(x,0) = 0,

z (0,y 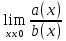) = 0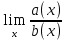.