Высшая математика. Вышка. 1. Определители и их свойства
 Скачать 242.71 Kb. Скачать 242.71 Kb.
|
|
25. Частные производные функции нескольких переменных. Частной производной функции z=f(x,y) по переменной X в точке P0(x0,y0) называется предел отношения частного приращения функции 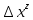 к соответствующему приращению аргумента к соответствующему приращению аргумента 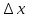 , когда последнее произвольным образом стремится к нулю. , когда последнее произвольным образом стремится к нулю.26.Дифференциал функции нескольких переменных Дифференциалом функции нескольких переменных наз. сумма произведений частных производных этой функции на приращения соответствующих независимых переменных, т.е. dz=z’xΔx+ z’yΔy Учитывая, что для функций f(x,y) = x и g(x,y) = y выполнено Δx=dx; y=dy′; Имеем dz= z’xdx+ z’ydy 27. Касательная плоскость к поверхности и нормаль. Если поверхность задана уравнением z=f(x;y), то на уравнение касательной плоскости будет получено как частный случай общего уравнения при F(x;y;z) = z-f(x;y). Тогда F’x=-f’x; F’y=-f’y ;F’z=1 и уравнение имеет вид: z-z0= f’x(M0)(x-x0)+ f’y(M0)(y-y0) Уравнения нормали будут 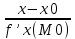 = = 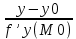 = = 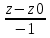 28. Экстремум функции двух переменных. Необходимое и достаточное условие. Точка M0(x0,y0) наз.точкой максимума (минимума) функции z= ƒ(𝑥, 𝑦)если существует такая окрестность точки M0 , что для всех точек 𝑀(𝑥, 𝑦) из этой окрестности, отличных от точки 𝑀0(𝑥0, 𝑦0), выполняется неравенство 𝑧(𝑀) < 𝑧(𝑀0) (𝑧(𝑀) > 𝑧(𝑀0)). Необходимое условие экстремума. Если непрерывная функция f(х) имеет в точке х0 экстремум, то в этой точке производная функции равна нулю (f '(х0) = 0) или не существует Точки, в которых производная функции равна нулю, называются стационарными. Стационарные точки и точки, в которых не существует производная, называются критическими точками функции. Достаточные условие экстремума. 1)Если производная функции при переходе через точку слева направо меняет знак, то х0 – точка локального экстремума. Если знак производной меняется с „+” на „–”, то х0 – точка max, если „–” на „+”, то х0 – точка min. 2) Пусть х0 – стационарная точка дважды непрерывно дифференц. в этой точке и некоторой ее окрестности функции f(х). Тогда, если f ''(х0)0, то х0 – точка локального min, если f ''(х0)>0, то х0 – точка локального max. (уравнений в системе столько же, сколько переменных в функции) 29. Наибольшее и наименьшее значение функции двух переменных в замкнутой области Пусть задана непрерывная на отрезке a,b, функции f(x) она достигает своих наибольших и наименьших значений либо во внутренних критических точках либо на концах отрезка a,b. Следует правило: 1.Найти критические точки принадлежащие данному отрезку. 2.Вычислить значение f(x) в критических точках и на концах отрезков 3.Выбрать из полученных значений max и min Пример:Найти наибольшее и наименьшее значение Y=x3- x2-x+2 на отрезке [0;2] Y’2=3x2-2x-1=0 => x1=1, x2= 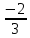 не принадлежит [0;2] не принадлежит [0;2]f(0)=2 ) max f(x)=f(2)=4 f(1)=1 } x ∈ [0;2] f(2)=4 ) min f(x)=f(1)=1, x ∈[0,2] 1) lim(x→x∞) 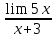 = = 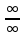 = = 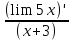 = lim(x→∞) = lim(x→∞)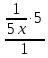 = = 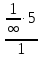 = 0 = 0 2) lim(x→0) 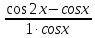 = = 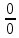 = lim(x→0) = lim(x→0)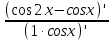 = lim(x→0) = lim(x→0) 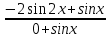 = lim(x→0) = lim(x→0) 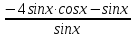 = = lim(x→0) = = lim(x→0) 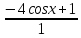 = -3 = -3 3) limx(x→0)ln 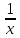 = = 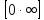 = lim(x→0) = lim(x→0)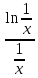 = =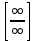 = lim(x→0) = lim(x→0) 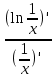 = lim(x→0) = lim(x→0)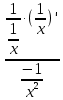 = lim(x→0) = lim(x→0) 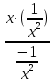 = lim(x→0)=0 = lim(x→0)=04) lim(x→0) ( 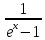 - - 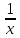 )= )=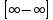 = lim(x→0) = lim(x→0)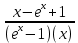 = =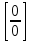 = lim(x→0) = lim(x→0) 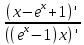 = lim(x→0) = lim(x→0)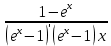 = =lim(x→0) 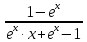 = =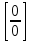 = lim(x→0) = lim(x→0) 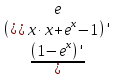 = lim(x→0) = lim(x→0)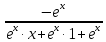 = lim(x→0) = lim(x→0)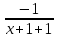 =- =-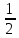 y=  D(y) x-5≠0 x≠5 D(y)=(-∞;5) 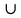 (5;+∞) (5;+∞)Функция элементарная ⇒ непрерывная в D(y) x=5 lim(x→5-0)  = =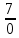 =∞; lim(x→5+0) =∞; lim(x→5+0) = =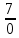 =+∞ =+∞ |
