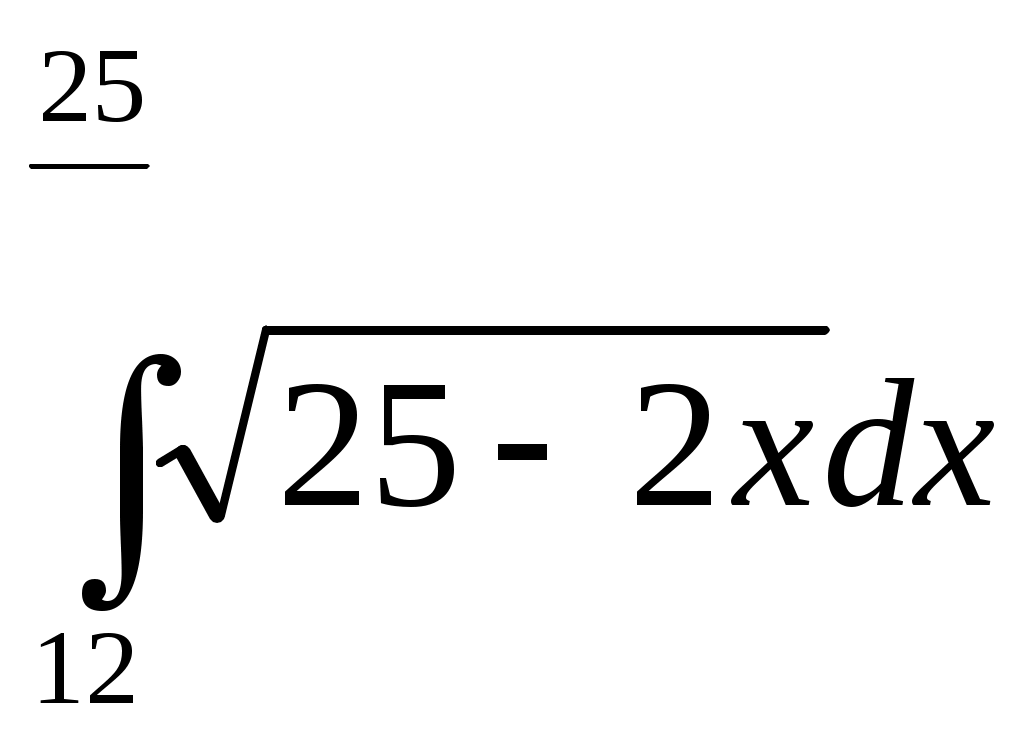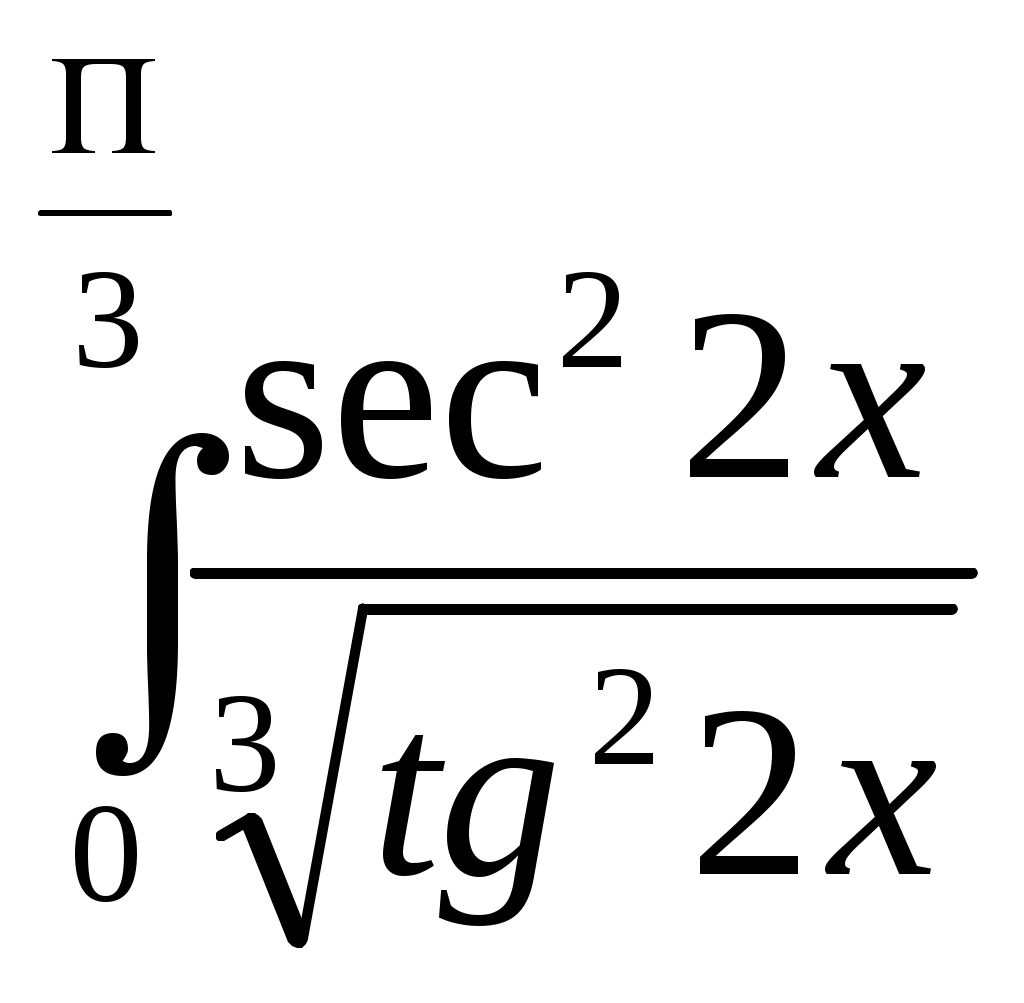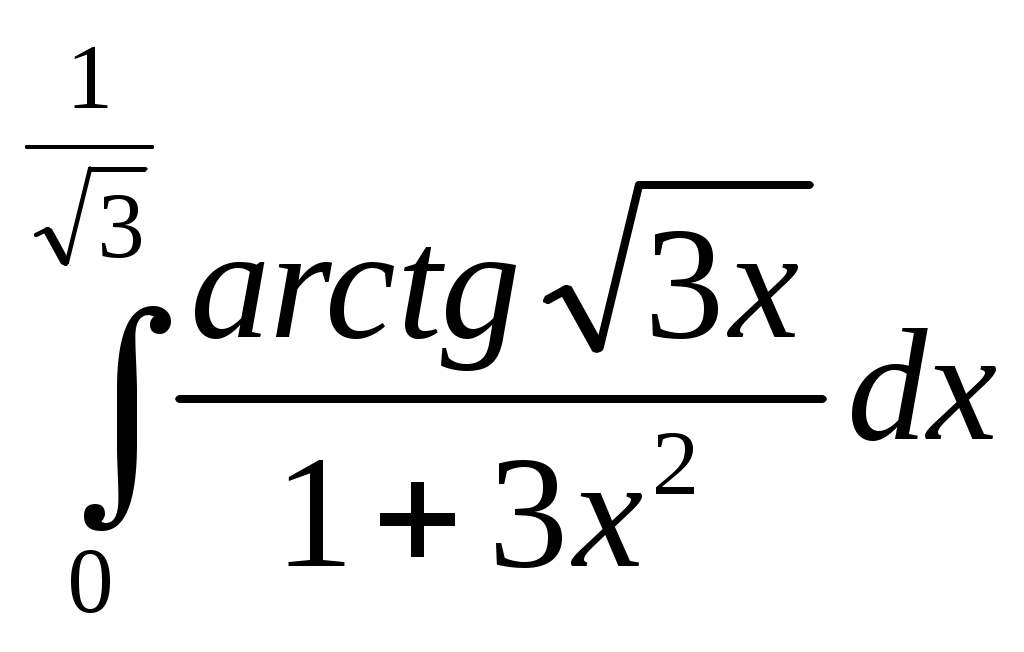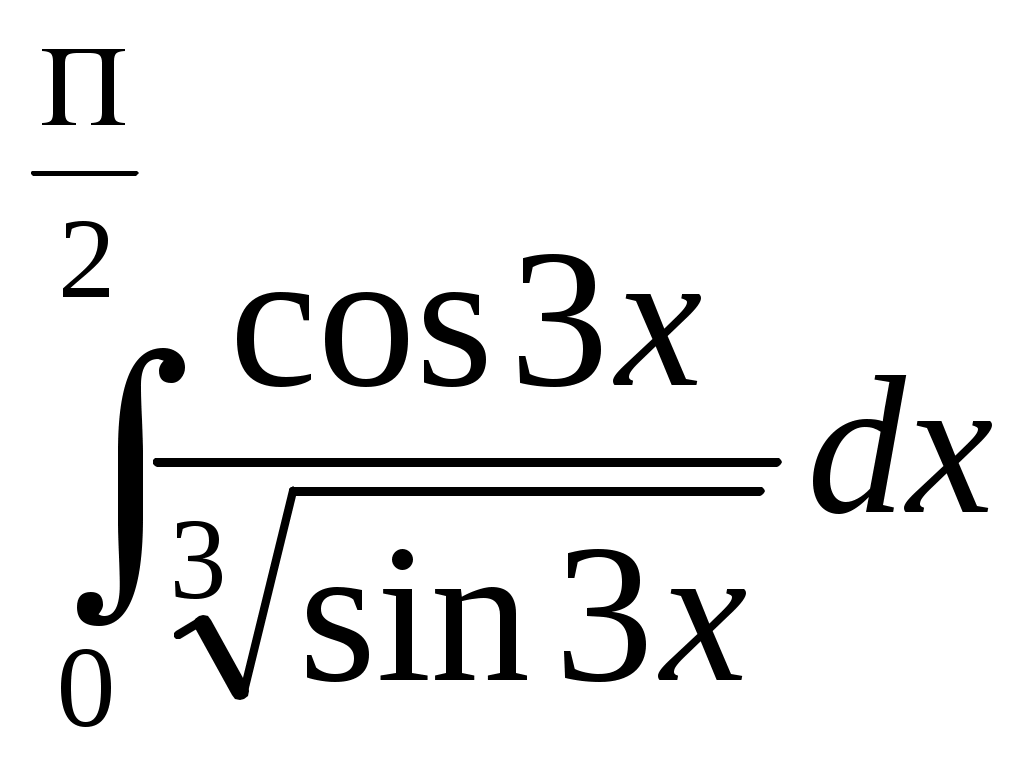Определенный интеграл. Определенный интеграл. Методические указания. Формула НьютонаЛейбница
 Скачать 0.79 Mb. Скачать 0.79 Mb.
|
|
4. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 4.1. Вычисление определенного интеграла. Формула Ньютона-ЛейбницаПусть функция у = ƒ (х) непрерывна на отрезке (а;в). Разобьем этот отрезок произвольным образом на n частичных отрезков длиною Δ х1 , Δ х2 ….. Δ хn ; выберем в каждом отрезке по одной произвольной точке ξ 1, ξ 2 …..ξn ; вычисление значения функции у = ƒ (х) в выбранных точках и составили сумму в выбранных точках и составили сумму: ƒ (ξ 1) Δ х1 + ƒ (ξ 2) Δ х2 + ƒ (ξ n) Δ хn = Эта сумма называется интегральной суммой функции ƒ (х) на отрезке (а;в). По-разному деля отрезок (а;в) на n частичных сумм и по-разному выбирая в них по одной точке ξί, получаем различные интегральные суммы. При неограниченном возрастании n и при стремлении к нулю наибольшей из длин частичных отрезков существует общий предел интегральных сумм. Этот общий предел всех интегральных сумм функции ƒ (х) на отрезке (а;в) называется определенным интегралом от ƒ (х) в пределах от а до в и обозначается Простейшие свойства определенного интеграла: При перестановке пределов изменяется знак интеграла: Интеграл с одинаковыми пределами равен нулю: Каковы бы ни были числа а,в,с имеет место равенство: Интеграл от суммы функций равен сумме интегралов: Постоянный множитель можно выносить за знак интеграла: Для вычисления определенного интеграла, когда можно найти соответствующий неопределенный интеграл, служит формула Ньютона-Лейбница: Пример 1 Вычислить интеграл:  Если функции и = и(х) и V = V(х) непрерывны вместе со своими производными на отрезке (а;в), то имеет место формула интегрирования по частям: Пример 2. Вычислить интеграл 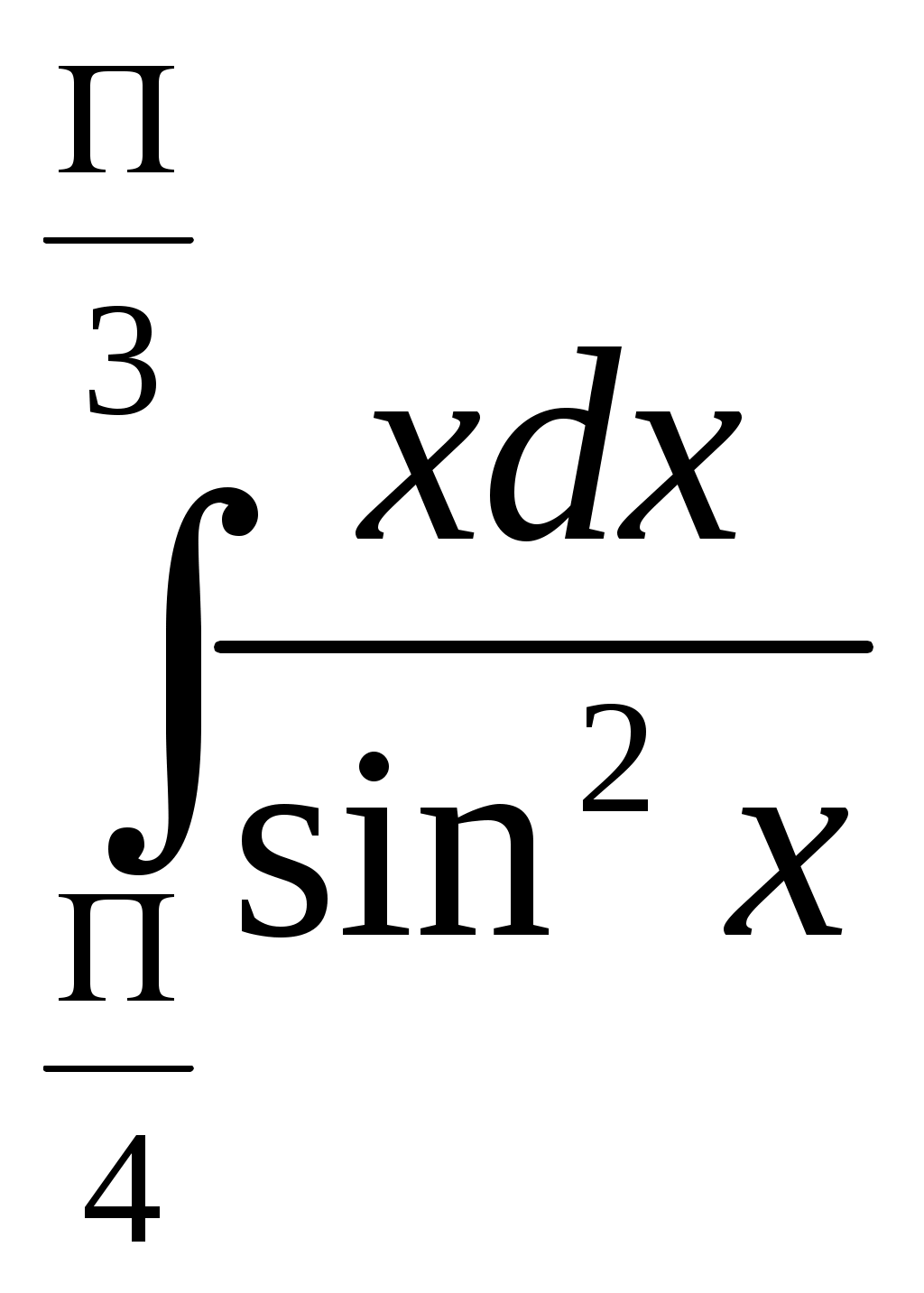 Решение Полагая и = х, dv = 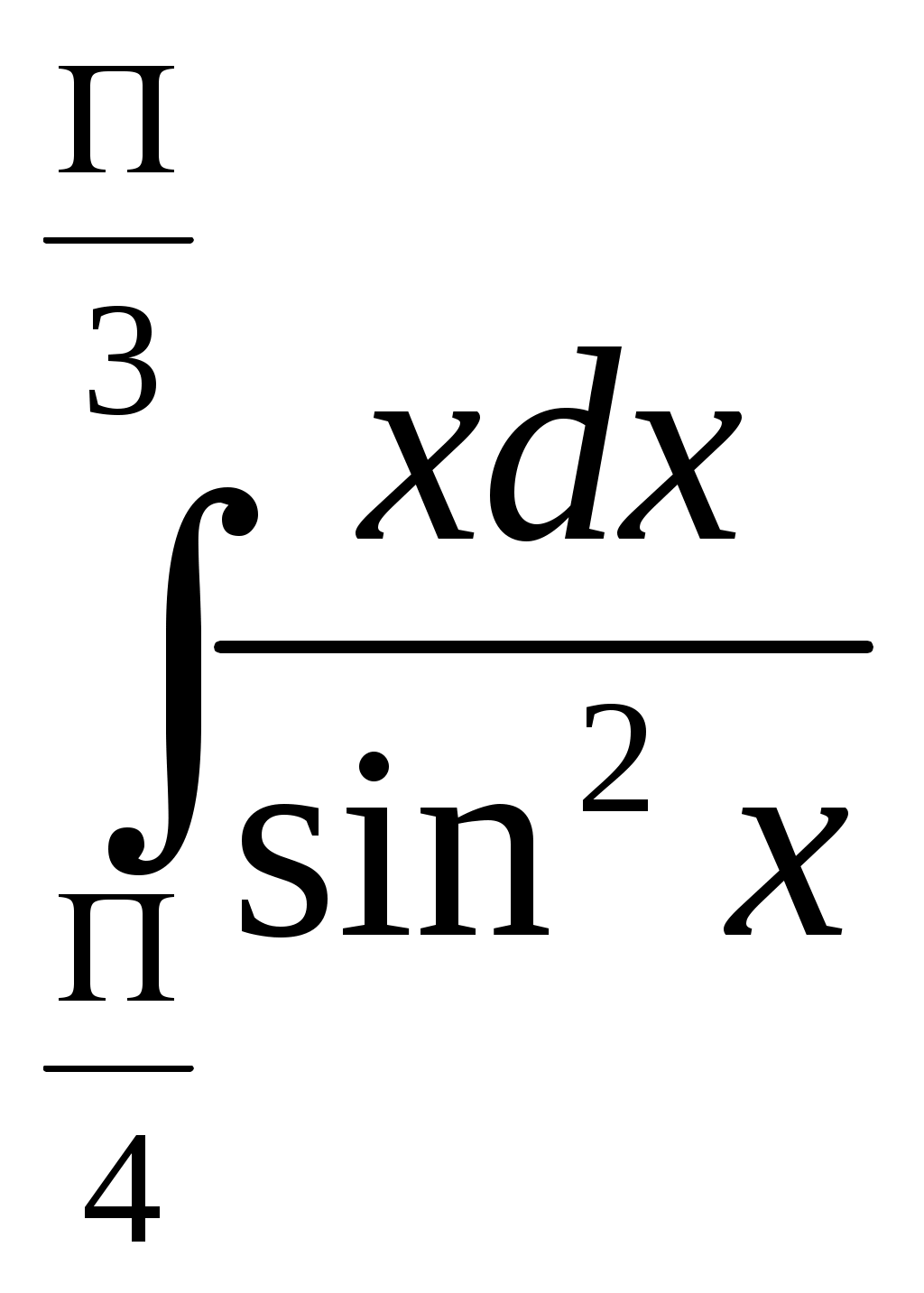 = (-x ctg x) │ - = (-x ctg x) │ - 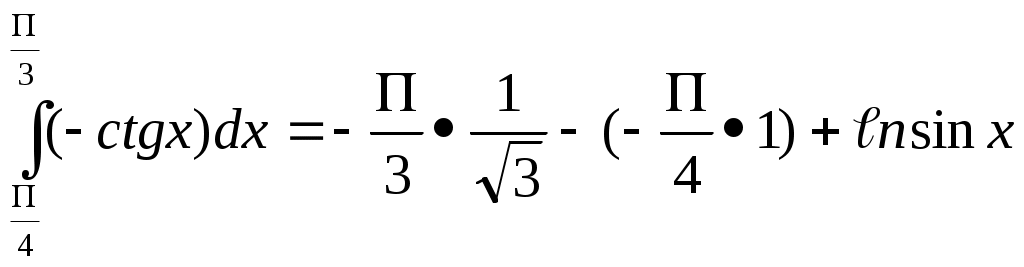 ││ ││Если функция f (х) непрерывна на отрезке (а;в), а функция х = φ(t) непрерывна и дифференцируема на отрезке (α; β). Причем φ(α) = а, φ(β) = в, то справедлива формула Пример 3. Вычислить интеграл: Решение Полагая х = 2 sin t, получим: dx = 2 cost dt, t1 = t2 = 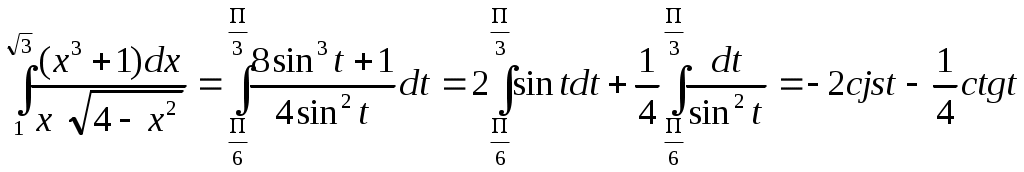 │ │РАЗДЕЛ А.
|