Определенный интеграл. Определенный интеграл. Методические указания. Формула НьютонаЛейбница

• Название: Формула НьютонаЛейбница
• Анкор: Определенный интеграл
• Дата: 03.05.2023
• Размер: 0.79 Mb.
• Имя файла: Определенный интеграл. Методические указания.doc
• Тип: Документы; #1106397
• страница: 4 из 5

РАЗДЕЛ А

Найти длину дуги кривой:

135. 
     у =
     
136. 
     у = от х = 0 до х =
     
137. 
     у = от 0 (0;0) до А (
     
138. 
     
     
139. 
     
     
140. 
     от А (0;0) до В (0;3П)
     
141. 
     р = 4 φ (двух первых витков)
     
142. 
     р = 3е^φ , х = 0 до х =
     
143. 
     р = 3 е ^φ , 0 ≤ φ ≤ 2ℓn3
     
144. 
     астроиды х =
     
145. 
     
     

РАЗДЕЛ Б

Найти длину дуги.

135. 
     , отсеченной прямой
     
136. 
     у² = (х+2)³, отсеченной осью оу
     
137. 
     у² = 2(х-4), отсеченной прямой х = 3у *
     

* здесь удобно принять у за независимую переменную

135. 
     , отсеченной осью ох
     
136. 
     у² = 4х между прямыми у = х и у =
     
137. 
     между точками (1;0) и ( )
     
138. 
     2у³ = х² между точками О (0;0)и В (8 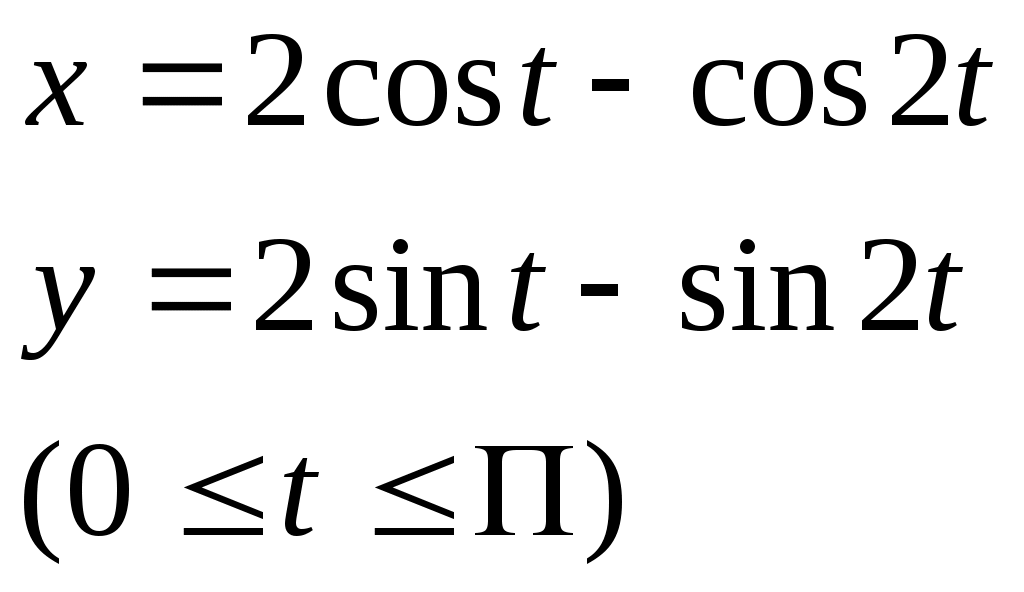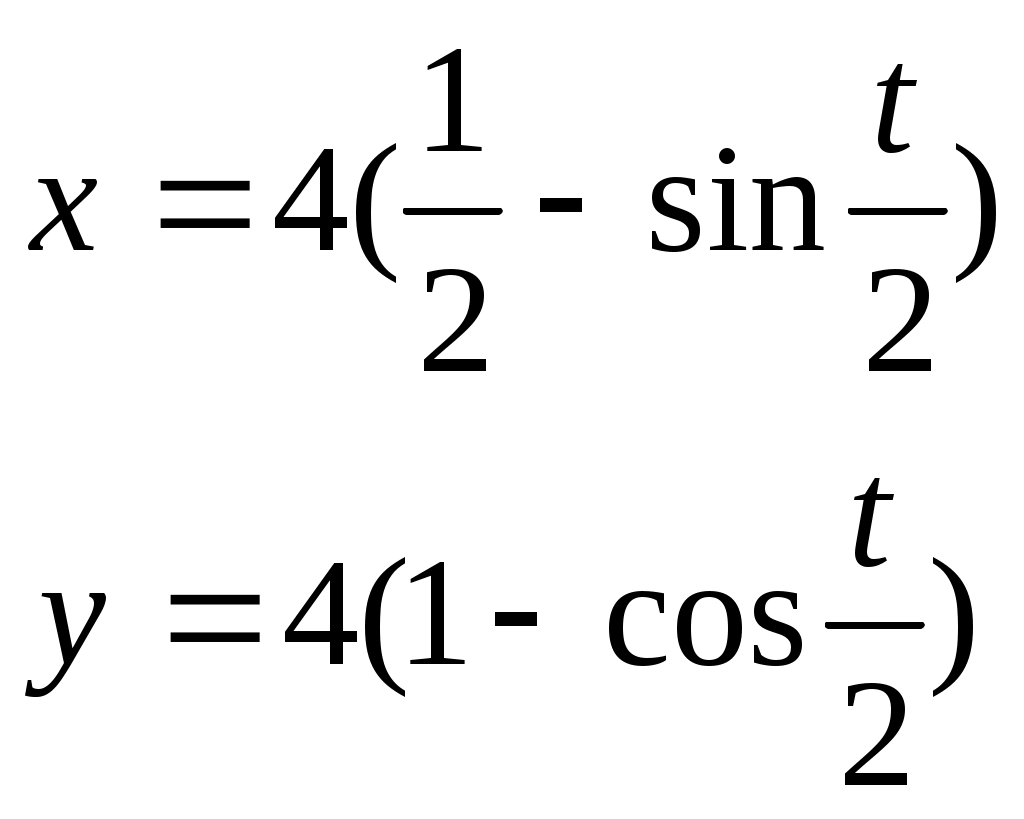; 4)*
     
139. 
     
     
140. 
     (0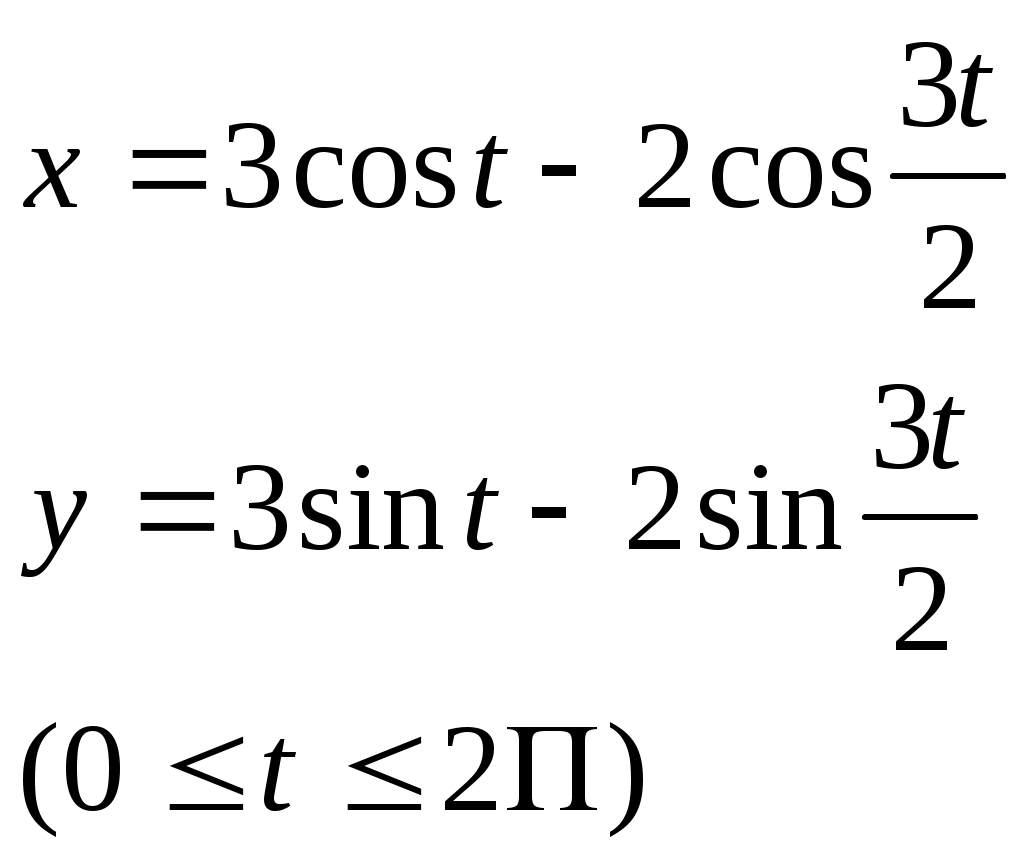
     
141. 
     
     
142. 
     (
     
143. 
     (0
     
144. 
     (петля)
     
145. 
     (
     
146. 
     (
     
147. 
     
     
148. 
     
     
149. 
     
     
150. 
     найти периметр фигуры, ограниченной кривыми у³ = х² и
     

у =

135. 
     Найти периметр фигуры ограниченной линиями х² = (у+1)³ и у=4
     
136. 
     Найти периметр одного из криволинейных треугольников, ограниченных осью абсцисс и линиями у = и .
     

4.4. Объем тела вращения

Если тело образовано вращением вокруг оси Ох криволинейной трапеции, которая ограничена графиком функции , прямыми х = а, х = в ( и осью ох (рис. 1), то его объем определяется по формуле



Если фигура, ограниченная графиком двух функций и ( на отрезке (а;в) и прямыми х = а, х = в (рис. 4) вращается вокруг оси Ох, то объем тела вращения будет равен



При вращении вокруг оси Оу криволинейной трапеции, изображенной на рис. 5 образуется тело вращения, объем которого равен



Пример 1. Вычислить объем тел, образованных вращением фигуры, ограниченной линиями у = х ² и х + у = 2 , у = 0 вокруг осей Ох и Оу.

Решение.

Ограниченная данными кривыми фигура ОАВ имеет вершины О (0;0) А (1;1) и В (2;0).

При вращении вокруг оси Ох (рис. 11) она образует тело, объем которого может быть найден как сумма объемов тел, образованных вращением трапеций ОСА и САВ вокруг оси Ох
Рис. 11





=



При вращении вокруг оси Оу (рис. 12) образуется тело, объем которого может быть найден как разность объемов тел, образованных вращением вокруг оси Оу криволинейных трапеций ОВАД и ОАД :



=



Объем тела вращения вокруг оси Ох трапеции, ограниченной линией 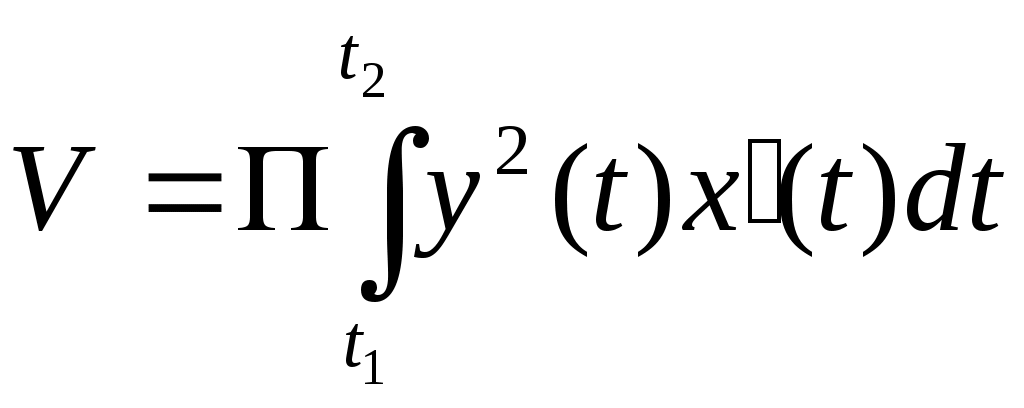, осью Ох и прямыми , вычисляется по формуле



Пример 2. Вычислить объем тела, образованного вращением вокруг оси Ох астроиды

Решение

Воспользуемся симметрией астроиды:
Рис.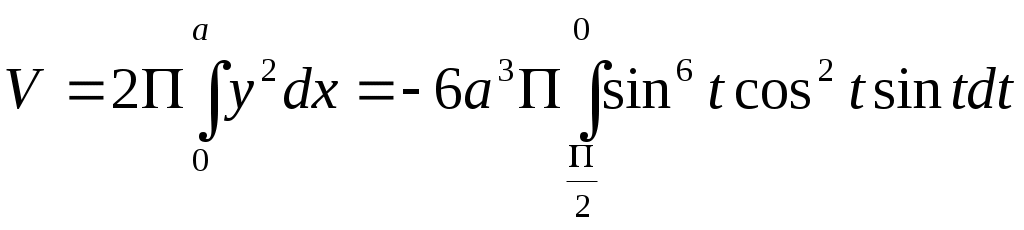



Преобразуем тождество под интегральное выражение и, применяя формулу интегрирования степени, получим: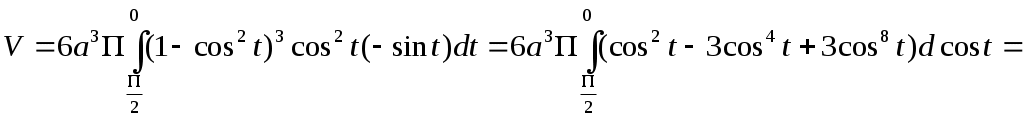




РАЗДЕЛ А
Найти объемы тел, образованных вращением фигуры, ограниченной заданными линиями:

а) относительно оси Ох

178. у = 4х – х² , у = 0 ;

179. ;

180. у = х² +1, у = 0 , х = 1, х = 2;

181. у = е^х , у = 0, х = 0, х = 1;

182. у = х² , у = ;

б) относительно оси Оу

183. ху = 4, х = 0 , у = 1, у = 4;

184. у = , у = у = ;

185. у = х³ , у = 1, х = 0;

186. у = 4 – х², у = 0, х = 0 (х );

187. х + у = 4, ху = 3;


РАЗДЕЛ Б
Найти объемы тел, образованных вращением фигуры, ограниченной заданными линиями:

а) относительно оси Ох

188. 
     у = - х, ху = -4, у = 0, х = -3;
     
189. 
     у = 4х + х², у = ;
     
190. 
     у = 3х – х², х + у – 3 = 0;
     
191. 
     у = , у = , у = 0, у = 1;
     
192. 
     у = е^2х , у = е^х, х = 2;
     
193. 
     у = , х = 3 , х = е;
     
194. 
     ;
     
195. 
     ;
     
196. 
     (астроида);
     
197. 
     у = 0,25 х² + 2, 5х – 8у + 14 = 0;
     
198. 
     у = е^х, у = е^-х , у = ;
     
199. 
     ;
     
200. 
     х² + у² = 2 у;
     
201. 
     ;
     
202. 
     у = 0, ;
     

б) относительно оси Оу

188. 
     у = , у = 0;
     
189. 
     у= х-1, у =0, у = -е^х, х = -1;
     
190. 
     ;
     
191. 
     ху = 3, х + у = 4;
     
192. 
     х² – у² = а², у = 2а, у = 0, (а );
     
193. 
     ху = 4, у = 1, у = 4, х =0;
     
194. 
     у = х³ , х =0, у = 8;
     
195. 
     у = х², 8х = у²;
     
196. 
     у =х³, у =0, х =2;
     
197. 
     х² – у² = 4, у = 2;
     
198. 
     у = х , х = 0;
     
199. 
     х = 4у – у², х =3;
     
200. 
     (у-1)² = 3х, у = 3 и х =0;
     
201. 
     и х = 3;
     
202. 
     у² = 4 – х и х = 0;
     
203. 
     у² + х – 4 = 0, х =0;
     
204. 
     у² = (х+4)³, х =0.
     

4.5. Несобственные интегралы

Интегралы с бесконечными пределами.
Интегралы с бесконечными пределами или от разрывных функций называются несобственными.

1. Несобственные интегралы с бесконечными пределами интегрирования определяются посредством предельного перехода:
;
;

;

где с – произвольное вещественное число.
2. Несобственные интегралы от функций с бесконечным разрывом также определяются посредством предельного перехода: если функция 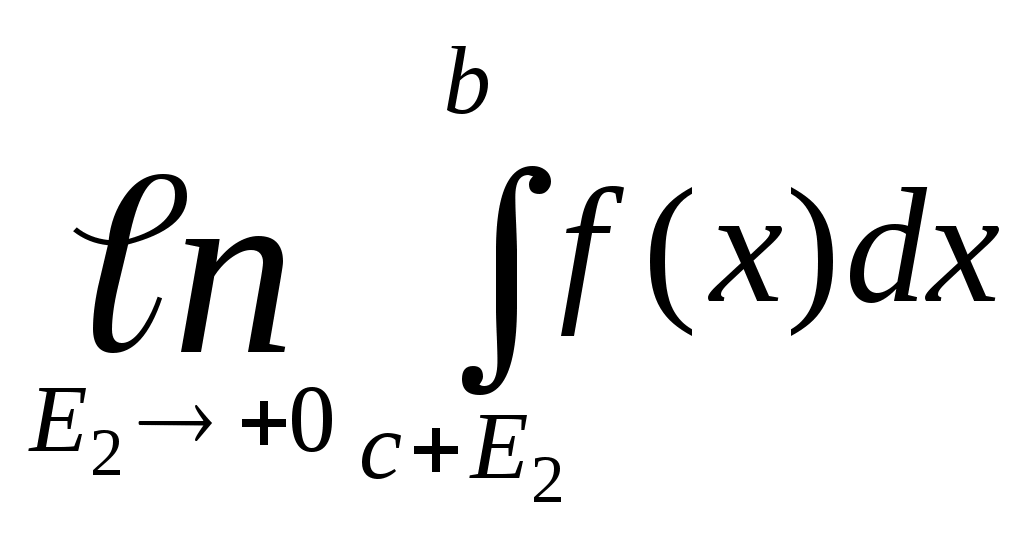имеет бесконечный разрыв в точке х = с, принадлежащей отрезку (а, в), и непрерывна во всех других точках этого отрезка, то
;

где Е₁ и Е₂ изменяются независимо друг от друга.

Несобственные интегралы называются сходящимися или расходящимися, смотря потому, существуют или нет определяющие их пределы соответствующих определенных интегралов.

Найти следующие несобственные интегралы или доказать их расходимость:

Пример 1

Решение

= =

следовательно, данный несобственный интеграл расходится.

Пример 2

Решение

= + =



следовательно, интеграл сходится.
Пример 3



Решение

Здесь х =2 – точка разрыва подинтегральной функции, поэтому используем предельный переход:

= =

=

исследуемый интеграл сходится.
С помощью замены предельной интегрирования несобственный интеграл в отдельных случаях преобразуется к обыкновенному определенному интегралу.

Пример 4. Найти несобственный интеграл



Решение

Преобразуем интеграл к новой переменной. Полагая 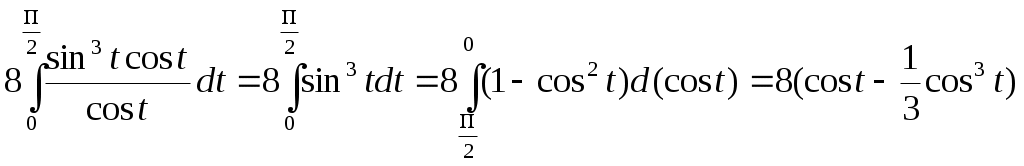, получим: ; при х =0; при х – 2,

= =

= .