Высшая математика. Вышка. 1. Определители и их свойства
 Скачать 242.71 Kb. Скачать 242.71 Kb.
|
|
1.Определители и их свойства. Определителем квадратной матрицы или просто определителем (детерминант) называется число, которое ставится в соответствие матрице и может быть вычислено по её элементам. 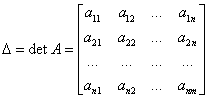 Свойства определитей 1.При транспонировании величина определителя не меняется. 2. Строки и столбцы определителя эквиваленты. Если в определители поменять местами какие-либо две строки (столбца) местами, то определитель меняет знак. 3: Определитель с двумя одинаковыми столбцами (строками) равен 0. При умножении элементов какого-либо столбца (строки) на число , определитель умножается на это число. Если все элементы какого-либо столбца (строки) равны 0 , то определитель равен 0. Если элементы двух строк (столбцов) пропорциональны, то определитель равен 0. Определитель не изменится, если к элементам какого-либо столбца (строки) прибавить соответствующие элементы другого столбца умноженного на одно и тоже число. 2. Матрицы: определение, виды матриц, действия с матрицами, обратная матрица.Определение. Матрица- это таблица чисел состоящая из n- строк и n- столбцов. Виды матриц.Определение. Матрица строка- это матрица которая содержит только одну строку. Матрица столбец- Матрица которая содержит только один столбец. Матрица квадратная- в которой количество строк равно количеству столбцов Нулевая Матрица- все элементы равны нулю Единичная Матрица- квадратная Матрица в которой все элементы главной диагонали равны единице, а остальные равны нулю Определитель (детерминант)матрицы называется определитель образованный из элемента данной матрицы Квадратная Матрица –наз. выражденной если её определитель равен нулю и не выражденной если определитель не равен нулю. Две матрицы одинакового размера наз. равными если равны их соответствующие элементы. Симметричная Матрица - это элементы которой удовлетворяют свойству a=aij при i≠j ДЕЙСТВИЯ С МАТРИЦАМИ: Умножение матрицы на число. Пример: Для того чтобы умножить матрицу на число, нужно каждый элемент матрицы умножить на данное число. В данном случае – на тройку. Умножать матрицы можно только тогда, когда число столбцов первой матрицы равно числу строк второй матрицы Транспонирование матрицы. Для того чтобы транспонировать матрицу, нужно ее строки записать в столбцы транспонированной матрицы. Пример: Транспонировать матрицу Сложение матрицСложение матриц (сумма матриц) Суммой матриц одинакового размера наз. Матрица С того же размера все элементы которой равны сумме соответствующих элементов матриц A и B сij = aij + bij Пример 1. Даны две матрицы одинакового размера. Вычитание матриц (разность матриц) A - B есть операция вычисления матрицы C сij = aij - bij Обратная матрица: Обратная матрица A−1 — матрица, произведение которой на исходную матрицу A равно единичной матрице E: A·A-1 = A-1·A = E E- единичная матрица того же размера, что и матрица А Свойства обратной матрицы
Определение. Минором Mij к элементу aij определителя n-го порядка наз. определитель (n - 1)-го порядка, полученный из исходного определителя вычеркиванием i-той строки и j-того столбца. Определение. Алгебраическим дополнением Aij к элементу aij определителя n-го порядка называется число Aij = (-1)i + j · Mij 3. Системы линейных алгебраических уравнений (СЛАУ) (в том числе –однородные СЛАУ). Системой n- линейных уравнений сn-неизвестными наз. Система вида:(вместо k--n)  Решением системы наз. Упорядоченный набор чисел который при подстановке в систему вместо неизвестных обращает все ур-ния в тождества. СЛАУ наз. однородной, если все свободные члены=0 . СЛАУ наз. не совместной если она не имеет решений. Совместная наз. определенной если она имеет единственное решение. Совместная система наз. неопределенной если она имеет бесконечное множество решений Матрица составленная из коэфф. Системы наз. основной матрицей СЛАУ. Матрица составленная из свободных членов наз. матрицей столбцов свободных СЛАУ Расширенная матрица системы- полученная из основной матрицы системы добавлением столбца свободным членом СЛАУ 4. Метод Гаусса решения СЛАУ (метод исключения неизвестных) Прямой ход – это приведение системы к ступенчатому виду. Обратный ход – это нахождение значений неизвестных. 5. Метод Крамера решения СЛАУ. Метод можно применить только в том случае , когда число ур-ний = числу наизв. И определитель основной матрицы системы = 0 Решить систему: (12х1+х2-х3=-31 ‹(3х1+5х2-4х3=2 (2х1-х2+3х3=1 Δ= 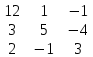 | | 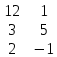 = 180- = 180-8+3+10-48-9=128 Δ1= 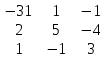 Δ2, Δ3 точно также Х1= 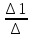 , х2, х3 также , х2, х3 также 6. Векторы, действия с ними. Модулем (абсолютной величиной) вектора наз. длина отрезка изображающего вектора. Вектор длина которого = 0 наз. нулевым вектором ( 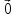 ). ).Вектор длина которого = 1 наз. единичной ( 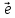 ) ) Два вектора наз. коллинеарными если сущ-ет прямая, которой они параллельны. Вектор наз. противоположным вектору, если они коллинеарные, противоположно направлены и одинаковой длины. Равные векторы- два вектора, если они коллинеарные, сонаправленные и имеют одинаковую длину. Действия с геометрическими векторами Правило сложения векторов по правилу треугольников 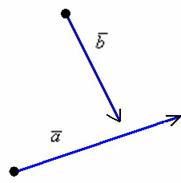 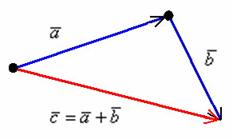 Вычитание векторов 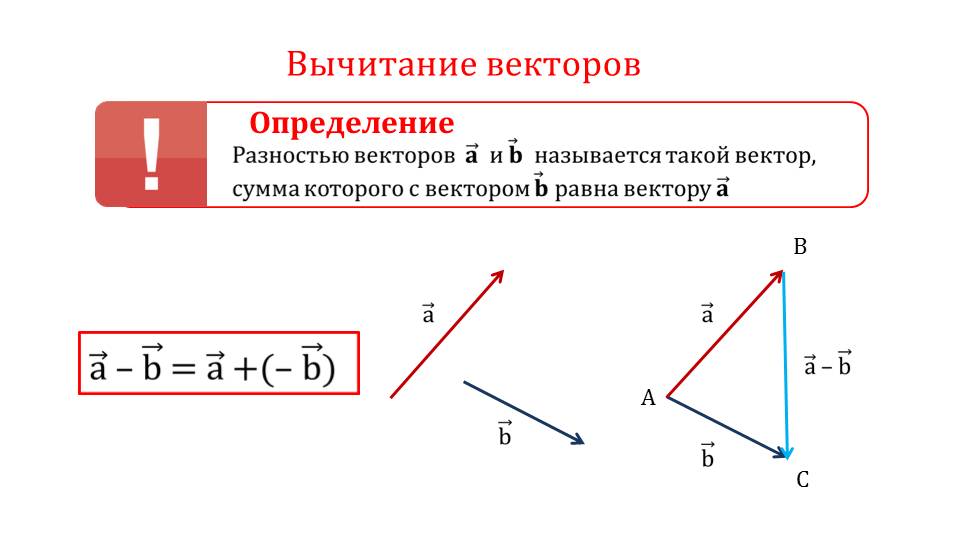 УмножениеДва вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Если стрелки данных векторов направлены в одинаковом направлении, то такие векторы называются сонаправленными Если стрелки смотрят в разные стороны, то векторы будут противоположно направлены. Обозначения: коллинеарность , (векторы сонаправлены) (векторы направлены противоположно). Правило умножения 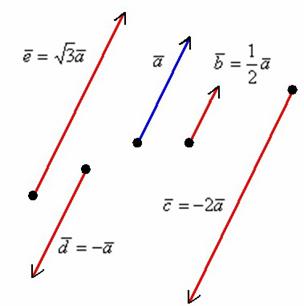 Действия с векторами в координатной форме 1. Умножение на число Если 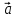 (ах,аy,аz) ʎ=const, то (ах,аy,аz) ʎ=const, то ʎ 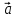 = (ʎах , ʎay , ʎaz ) = (ʎах , ʎay , ʎaz )2. Сложение(вычитание) векторов если 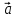 = (ах,аy,аz), = (ах,аy,аz), 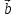 = (bх,by,bz), то = (bх,by,bz), то 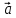 ± ±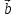 (ах±bx,±аy±by,az±bz) (ах±bx,±аy±by,az±bz)3. Условие коллинеарности векторов если 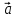 = (ах,аy,аz) b ⃗ = (bх,by,bz), а||b то = (ах,аy,аz) b ⃗ = (bх,by,bz), а||b то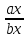 = =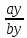 = =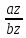 = =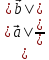 7.Скалярное произведение векторов и его свойства. Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла между ними. 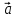 · ·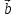 =| =|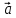 || ||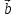 |cos |cos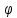 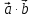 =| =|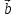 |ПР |ПР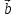 - -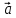 =| =|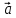 |ПР |ПР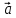 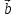 пр-а пр-а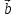 = =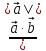 , пр-b , пр-b 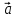 = =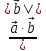 |
