Вектор это направленный отрезок прямой. Коллинеарные
 Скачать 466.84 Kb. Скачать 466.84 Kb.
|
1 2
7.Векторы. Коллинеарные и компланарные векторы. Линейные операции над векторами, их свойства. Разложение вектора по двум неколлинеарным векторам. Разложение вектора по трем некомпланарным векторам. Вектор – это направленный отрезок прямой. Коллинеарные векторы Сонаправлены и их длины равны. Компланарные векторы Лежат на одной или параллельных прямых. Появилось новое понятие о векторах в пространстве, которого не было на плоскости - компланарность векторов.Быстрый ответ Линейными операциями над векторами называются операции сложения (вычитания) векторов и умножения вектора на число. оммутативность; + Разложение вектора по двум неколлинеарным векторам.= x + y, (3) где x и y — некоторые числа, то говорят, что вектор разложен по векторам и. Числа x и y называются коэффициентами разложения вектора по векторам и. Любой вектор m может быть представлен, и притом единственным образом, в виде линейной комбинации трех любых некомпланарных векторов а, b и с: 8.Проекция вектора на ось. Угол между вектором и осью. Координаты вектора. Направляющие косинусы вектора. Линейные операции над векторами в координатной форме. Проекция вектора на ось — это длина отрезка, заключенного между проекциями начала и конца вектора на эту ось, взятая со знаком «+» или «-». Если угол между вектором и осью острый, то его проекция на эту ось положительна, если угол тупой — отрицательна, если прямой — равна нулю Углом между вектором и осью называется угол между данным вектором и любым правоориентированным вектором этой оси. рис.2. Обозначение. п.2. Проекция вектора на ось. Координатами вектора с началом в точке A (x 1; y 1) и концом в точке B (x 2; y 2) называются числа a 1 = x 2 — x 1; a 2 = y 2 — y 1. Таким образом, чтобы найти координаты вектора, надо из координат его конца вычесть координаты начала. – это косинусы углов, которые вектор образует с положительными полуосями координат. 1) сложение: ; 2) вычитание: ; 3) умножение вектора на число: , где k-число (скаляр). 9.Базис в пространстве, на плоскости, на прямой. Прямоугольный декартовый базис. Базисом в пространстве называются произвольные три некомпланарных вектора, которые взяты в определенной последовательности.Базисом на прямой называется любой ненулевой вектор на этой прямой. Любой другой вектор, коллинеарный данной прямой, может быть выражен через вектор в виде. Базис называется прямоугольным декартовым, если базисные векторы взаимно перпендикулярны и l=1 каждого. Такой базис принято обозначать (i, j, k). 10.Скалярное произведение векторов, его свойства. Выражение скалярного произведения через координаты. Некоторые приложения скалярного произведения (угол между векторами, проекция вектора на заданное направление). Скалярным произведением двух векторови называется число, равное произведению модулей векторов и на косинус угла между ними. Скалярное произведение имеет следующие свойства: 1.Скалярное произведение коммутативно, то есть для любых векторов 2. 3. Скалярное произведение равно нулю тогда и только тогда, когда сомножители ортогональны или хотя бы один из них равен нулю. 4. Скалярное произведение ассоциативно относительно скалярного множителя, то есть 5. Скалярное произведение дистрибутивный относительно сложения, то есть для произвольных трех векторов 6. Векторы ортонормального базиса удовлетворяют соотношениям: В ортонормированном базисе скалярное произведение векторов равно сумме произведений одноименных координат векторов: 11.Векторное произведение векторов, его свойства. Выражение векторного произведения через координаты. Некоторые приложения векторного произведения (установление коллинеарности векторов, нахождение площади параллелограмма и треугольника). Векторным произведением вектора на вектор называется вектор (рис. 2.15), у которого: 1) длина численно равняется площади параллелограмма, построенного на этих векторах. 1) 2) 3) +4) Итак, векторное произведение через координаты сомножителей выража-ется определителем третьего порядка, составленным из базисных векторов и координат перемножаемых векторов. Вычисление площади параллелограмма и треугольника, условие коллинеарности двух векторов. 12.Смешанное произведение векторов, его геометрический смысл. Свойства смешанного произведения. Выражение смешанного произведения через координаты. Некоторые приложения смешанного произведения (определение взаимной ориентации векторов в пространстве, установление компланарности векторов, определение объема параллелепипеда). Смешанным произведением трех векторов, называется число, равное скалярному произведению вектора на вектор: Геометрический смысл смешанного произведения. Геометрический смысл смешанного произведения: если тройка векторов правая, то их смешанное произведение равно объему параллелепипеда построенного на этих векторах:. В случае левой тройки смешанное произведение указанных векторов равно объему параллелепипеда со знаком минус. 1. Модуль смешанного произведения некомпланарных векторов равен объему параллелепипеда, построенного на этих векторах. Произведение положительно, если тройка векторов — правая, и отрицательно, если тройка — левая, и наоборот. 2. Смешанное произведение равно нулю тогда и только тогда, когда векторы компланарны:векторы компланарны Найдем их смешанное произведение, используя выражение в координатах для векторного и скалярного произведений: 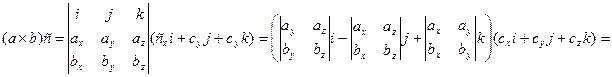 = 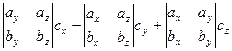 (1) (1)Полученную формулу можно записать в виде: 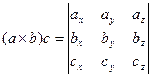 Следовательно, смешанное произведение векторов равно определителю третьего порядка, составленному из координат перемножаемых векторов. Некоторые приложения смешанного произведения. 1) Определение взаимной ориентации векторов в пространстве. Если abc>0 , то a,b,c – правая тройка Если abc<0, то a,b,c – левая тройка 2) Установление компланарности векторов. a,b,c – компланарны, когда их смешанное произведение равно 0. (аbc=0) 3) Определение объема параллепипеда и треугольной пирамиды. ; 13) Виды: A x + B y + C = 0,x /a + y /b = 1, y = k ⋅ x + b,x − x 1- a x = y − y 1/ a y, Углом между двумя пересекающимися прямыми называется величина наименьшего плоского угла при пересечении данных прямых. Итак, две плоскости параллельны друг другу тогда и только тогда, когда коэффициенты при соответствующих координатах пропорциональны Ясно, что две плоскости перпендикулярны тогда и только тогда, когда их нормальные векторы перпендикулярны, а следовательно, или . Расстояние от точки до прямой - это длина перпендикуляра (т.е. наименьшее расстояние), проведенного из данной точки к данной прямой.M1H1|= √ (x2-x1)^2+(y2-y1)^2 . 14) Окру́жность — замкнутая плоская кривая, которая состоит из всех точек на плоскости, равноудалённых от заданной точки, лежащей в той же плоскости, что и кривая: эта точка называется центром окружности. Отрезок, соединяющий центр с какой-либо точкой окружности, называется радиусом; радиусом называется также и длина этого отрезка. 15)Эллипс – это множество всех точек плоскости, сумма расстояний до каждой из которых от двух данных точек , называемых фокусами эллипса, – есть величина постоянная, численно равная длине большой оси этого эллипса: . При этом расстояния между фокусами меньше данного значения: эксцентриситет любой окружности равен нулю. 16)Каноническое уравнение гиперболы имеет вид расстояние от центра симметрии до каждого из фокусов рассчитывается по формуле: Эксцентриситетом гиперболы называют отношение Для гиперболы асимптотами являются оси абсцисс и ординат. Кривая может приближаться к своей асимптоте, оставаясь с одной стороны от неё 17)Параболой называется линия, которая в некоторой декартовой прямоугольной системе координат определяется каноническим уравнением y2=2px Фокусом параболы называется точка FF с координатами (p/2,0)(p/2,0) в канонической системе координат. 18) Если две плоскости (α1 и α2) заданы общими уравнениями вида: A1x+B1y+C1z+D1=0 и A2x+B2y+C2z+D2=0, то очевидно, что угол между ними равен углу между их нормалями, то есть между векторами n1={A1,B1,C1) и n2={A2,B2,C2). Получаем, что косинус угла между плоскостями α1 и α2 равен 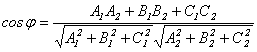 (1) (1)Условие параллельности плоскостей заключается в параллельности нормалей: (2) а условие перпендикулярности плоскостей – в перпендикулярности нормалей или равенстве нулю их скалярного произведения: A1A2 + B1B2 + C1C2 = 0. (3) d= A 2 +B 2 +C 2A⋅x M+B⋅y M+C⋅z M+D, гдеA , B , C , D A, B, C, DA,B,C,D —коэффициенты, задающиеплоскость, а ( x M , y M , z M ) (x_M, y_M, z_M)(x M,y M,z M) — координаты точки M MM. 19)  канонические ур-е прямых. канонические ур-е прямых.адача определения угламежду этими прямыми сводится к определению угла j между их направляющими векторами (m1;n1;p1) и (m2;n2;p2). По определению скалярного произведения:  Условие параллельности прямых L1 и L2, эквивалентное условию коллинарности векторов (m1;n1;p1) и (m2;n2;p2), заключается в пропорциональности координат их направляющих векторов:  Условие перпендикулярности прямых L1 и L2 выражается равенством нулю скалярного произведения векторов и : m1m2+n1n2+p1p2=0. 20) Углом между прямой и плоскостью называется любой из двух смежных углов, образованных прямой и ее проекцией на плоскость. Обозначим через угол между плоскостью и прямой.  Если прямая L параллельна плоскости Q, то векторы n и S перпендикулярны, а потому 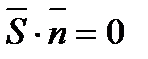 , т.е. , т.е.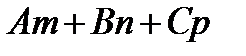 =0 является условием параллельности прямой и плоскости. =0 является условием параллельности прямой и плоскости.Если прямая L перпендикулярна плоскости Q, то векторы n и S параллельны. Поэтому равенства 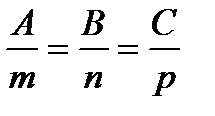 являются условиями перпендикулярности прямой и плоскости. являются условиями перпендикулярности прямой и плоскости.21)Множества, элементами которых являются числа. Такие множества называются числовыми. Виды: натуральные, целые, рациональные, все действительные Окрестностью точки х0 называется любой интервал (a; b), содержащий точку х0. В частности, интервал (х0-e; х0+e), где e>0 называется e-окрестностью точки х0. Число х0 называется центром, а число e — радиусом. Если хÎ(х0-e; х0+e), то выполняется неравенство х0-e<х<х0+e, или, что то же, |х-х0|<e. Выполнение последнего неравенства означает попадание точки х0 в e-окрестностью точки х0. Проколотой окрестностью точки х0 называется такая окрестность точки х0, из которой удалена сама точка х0. 22)Если хотите, комплексное число – это двумерное число. Оно имеет вид , где и – действительные числа, – так называемая мнимая единица. Число называется действительной частью ( ) комплексного числа , число называется мнимой частью ( ) комплексного числа . 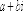 – это ЕДИНОЕ ЧИСЛО, а не сложение. Действительную и мнимую части комплексного числа, в принципе, можно переставить местами: или переставить мнимую единицу: – от этого комплексное число не изменится. Но стандартно комплексное число принято записывать именно в таком порядке: – это ЕДИНОЕ ЧИСЛО, а не сложение. Действительную и мнимую части комплексного числа, в принципе, можно переставить местами: или переставить мнимую единицу: – от этого комплексное число не изменится. Но стандартно комплексное число принято записывать именно в таком порядке: Действия над компл ч. Вычитание комплексных чисел Пример 2 Найти разности комплексных чисел и , если , Действие аналогично сложению, единственная особенность состоит в том, что вычитаемое нужно взять в скобки, а затем – стандартно раскрыть эти скобки со сменой знака: Результат не должен смущать, у полученного числа две, а не три части. Просто действительная часть – составная: . Для наглядности ответ можно переписать так: . Рассчитаем вторую разность: Здесь действительная часть тоже составная: Чтобы не было какой-то недосказанности, приведу короткий пример с «нехорошей» мнимой частью: . Вот здесь без скобок уже не обойтись. Умножение комплексных чисел Настал момент познакомить вас со знаменитым равенством: Пример 3 Найти произведение комплексных чисел , Очевидно, что произведение следует записать так: Что напрашивается? Напрашивается раскрыть скобки по правилу умножения многочленов. Так и нужно сделать! Все алгебраические действия вам знакомы, главное, помнить, что и быть внимательным. Повторим, omg, школьное правило умножения многочленов: Чтобы умножить многочлен на многочлен нужно каждый член одного многочлена умножить на каждый член другого многочлена. Я распишу подробно: Надеюсь, всем было понятно, что Внимание, и еще раз внимание, чаще всего ошибку допускают в знаках. Как и сумма, произведение комплексных чисел перестановочно, то есть справедливо равенство: . В учебной литературе и на просторах Сети легко найти специальную формулу для вычисления произведения комплексных чисел. Если хотите, пользуйтесь, но мне кажется, что подход с умножением многочленов универсальнее и понятнее. Формулу приводить не буду, считаю, что в данном случае – это забивание головы опилками. Деление комплексных чисел Пример 4 Даны комплексные числа , . Найти частное . Составим частное: Деление чисел осуществляется методом умножения знаменателя и числителя на сопряженное знаменателю выражение. Вспоминаем бородатую формулу и смотрим на наш знаменатель: . В знаменателе уже есть , поэтому сопряженным выражением в данном случае является , то есть Согласно правилу, знаменатель нужно умножить на , и, чтобы ничего не изменилось, домножить числитель на то же самое число : Далее в числителе нужно раскрыть скобки (перемножить два числа по правилу, рассмотренному в предыдущем пункте). А в знаменателе воспользоваться формулой (помним, что и не путаемся в знаках!!!). Распишу подробно: 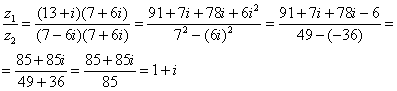 Пример я подобрал «хороший», если взять два числа «от балды», то в результате деления почти всегда получатся дроби, что-нибудь вроде . В ряде случаев перед делением дробь целесообразно упростить, например, рассмотрим частное чисел: . Перед делением избавляемся от лишних минусов: в числителе и в знаменателе выносим минусы за скобки и сокращаем эти минусы: Редко, но встречается такое задание: Пример 5 Дано комплексное число . Записать данное число в алгебраической форме (т.е. в форме ). Приём тот же самый – умножаем знаменатель и числитель на сопряженное знаменателю выражение. Снова смотрим на формулу . В знаменателе уже есть , поэтому знаменатель и числитель нужно домножить на сопряженное выражение , то есть на : Тригонометрическая и показательная форма комплексного числа В данном параграфе больше речь пойдет о тригонометрической форме комплексного числа. Показательная форма в практических заданиях встречается значительно реже. Рекомендую закачать и по возможности распечатать тригонометрические таблицы, методический материал можно найти на странице Математические формулы и таблицы. Без таблиц далеко не уехать. Любое комплексное число (кроме нуля) можно записать в тригонометрической форме: , где – это модуль комплексного числа, а – аргумент комплексного числа. Не разбегаемся, всё проще, чем кажется. Изобразим на комплексной плоскости число . Для определённости и простоты объяснений расположим его в первой координатной четверти, т.е. считаем, что : Модулем комплексного числа называется расстояние от начала координат до соответствующей точки комплексной плоскости. Попросту говоря, модуль – это длина радиус-вектора, который на чертеже обозначен красным цветом. Модуль комплексного числа стандартно обозначают: или По теореме Пифагора легко вывести формулу для нахождения модуля комплексного числа: . Данная формула справедлива для любых значений «а» и «бэ». Примечание: модуль комплексного числа представляет собой обобщение понятия модуля действительного числа, как расстояния от точки до начала координат. Аргументом комплексного числа называется угол между положительной полуосью действительной оси и радиус-вектором, проведенным из начала координат к соответствующей точке. Аргумент не определён для единственного числа: . Рассматриваемый принцип фактически схож с полярными координатами, где полярный радиус и полярный угол однозначно определяют точку. Аргумент комплексного числа стандартно обозначают: или Из геометрических соображений получается следующая формула для нахождения аргумента: . Внимание! Данная формула работает только в правой полуплоскости! Если комплексное число располагается не в 1-й и не 4-й координатной четверти, то формула будет немного другой. Эти случаи мы тоже разберем. Но сначала рассмотрим простейшие примеры, когда комплексные числа располагаются на координатных осях. Пример 7 Представить в тригонометрической форме комплексные числа: , , , . Выполним чертёж: 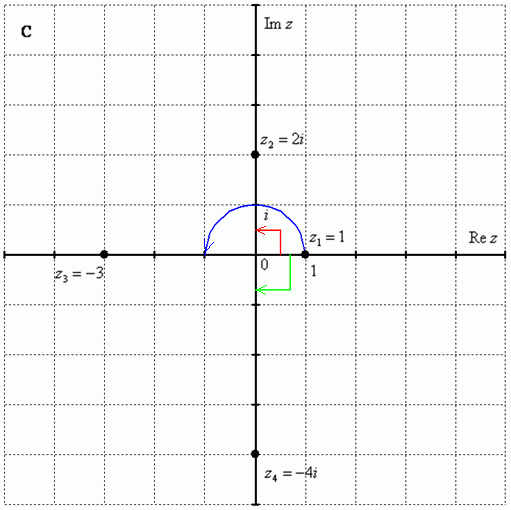 На самом деле задание устное. Для наглядности перепишу тригонометрическую форму комплексного числа: Запомним намертво, модуль – длина (которая всегда неотрицательна), аргумент – угол. 1) Представим в тригонометрической форме число . Найдем его модуль и аргумент. Очевидно, что . Формальный расчет по формуле: . Очевидно, что (число лежит непосредственно на действительной положительной полуоси). Таким образом, число в тригонометрической форме: . Ясно, как день, обратное проверочное действие: 23)Предел функции в точке – одно из основных понятий математического анализа. Преде́л фу́нкции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится значение рассматриваемой функции при стремлении её аргумента к данной точке. Я ебу чо такой вопрос длиный 24)Если существует предел , то функция называется бесконечно малой в точке . Существенным моментом утверждения является тот факт, что функция может быть бесконечно малой лишь в конкретной точке. Начертим знакомую линию : 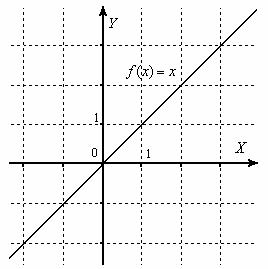 Данная функция бесконечно малА в единственной точке: Следует отметить что, в точках «плюс бесконечность» и «минус бесконечность» эта же функция будет уже бесконечно большой: . Или в более компактной записи: Во всех других точках, предел функции будет равен конечному числу, отличному от нуля. Таким образом, не существует такого понятия как «просто бесконечно малая функция» или «просто бесконечно большая функция». Функция может быть бесконечно малой или бесконечно большой только в конкретной точке. Функции Раскрытие неопределённости вида Если существует 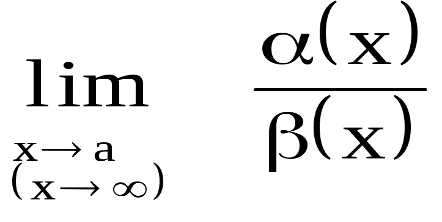 , то существует и , то существует и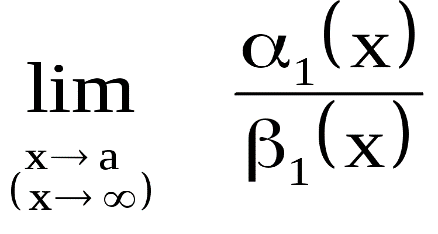 , ,причём 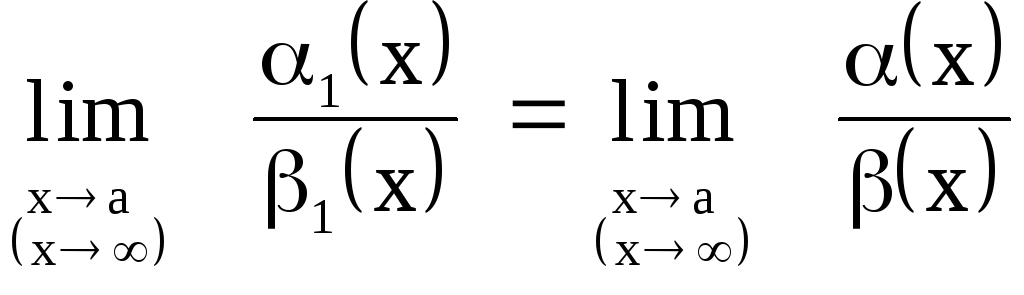 . .Это утверждение называется принципом замены бесконечно малых. Первый замечательный предел имеет вид Вместо переменной х могут присутствовать различные функции, главное, чтобы они стремились к 0. Пример. Необходимо вычислить предел Как видно, данный предел очень похож на первый замечательный, но это не совсем так. Вообще, если Вы замечаете в пределе sin, то надо сразу задуматься о том, возможно ли применение первого замечательного предела. Согласно нашему правилу №1 подставим вместо х ноль: Получаем неопределенность Теперь попробуем самостоятельно организовать первый замечательный предел. Для этого проведем нехитрую комбинацию: 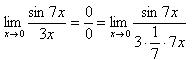 Таким образом мы организовываем числитель и знаменатель так, чтобы выделить 7х. Вот уже и проявился знакомый замечательный предел. Желательно при решении выделять его: 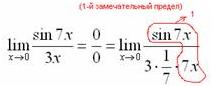 Подставим решение первого замечательного примера и получаем: 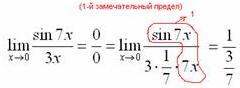 Упрощаем дробь: 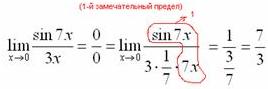 Ответ: 7/3. Как видите – все очень просто. Второй замечательный предел имеет вид Вместо переменной х могут присутствовать различные функции, главное, чтобы они стремились к Пример. Необходимо вычислить предел 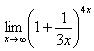 Здесь мы видим наличие степени под знаком предела, значит возможно применение второго замечательного предела. Как всегда воспользуемся правилом №1 – подставим Видно, что при х Воспользуемся вторым замечательным пределом для раскрытия нашей неопределенности, но сначала надо его организовать. Как видно – надо добиться присутствия в показателе, для чего возведем основание в степень 3х, и одновременно в степень 1/3x, чтобы выражение не менялось: 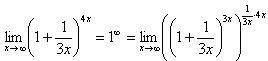 Не забываем выделять наш замечательный предел:  Дальше знак предела перемещаем в показатель:  Ответ: 25)Функция у = f(x) называется непрерывной в точке , если существует предел функции в этой точке и он равен значению функции в этой точке, т. е. Непрерывноть функции через преращение:  Функция у=f(x) называется непрерывной в точке , если она определена в точке хо и ее окрестности и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, т.е. . Функция у=f(x) называется непрерывной в точке , если она определена в точке хо и ее окрестности и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, т.е. .Точками разрыва функции называются точки, в которых функция не обладает свойством непрерывности. Классификация точек разрыва: 1. Точки разрыва первого рода (скачок) – точка если фукнция имеет конечные но не равные односторонние пределы. ( Пример: 2. Точки разрыва второго рода (бесконечный разрыв) - очка если хотя бы один из односторонних пределов бесконечен или несуществует. Примет: Под односторонним пределом числовой функции подразумевают «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левосторонним пределом (или пределом слева) (рис. 1) и правосторонним пределом (пределом справа) (рис. 2). 26)производной функции в точке называется предел отношения приращения функции к вызвавшему его приращению аргумента в этой точке при . Или коротко: производная функции в точке численно равна тангенсу угла наклона касательной к графику функции в данной точке: . А тангенс угла наклона касательной – это в точности её угловой коэффициент: Ур-е касательнойy=kx+b 27) Односторонние производные функции Односторонними производными называются односторонние предел. Для существования производной функции y f (x) в точке x необходимо и достаточно существование и равенство односторонних производных функции в точке x . Это функция, у которой существует дифференциал. Дифференцируемая на некотором множестве функция - это функция, дифференцируемая в каждой точке данного множества. Теорема. Если функция y = f(x) дифференцируема в некоторой точке x0, то она в этой точке непрерывна.
Пример 1 Найдем производную функции y(x) = (3 + 2x2)4. Заменим 3 + 2x2 на u и тогда получим y = u4. Согласно приведенному выше правилу дифференцирования сложных функций у нас получится: y = y′u ⋅u′x = 4u3 ⋅u'x А теперь выполним обратную замену и подставим исходное выражение: 4u3 ⋅u′x = 4 (3 + 2x2)3 ⋅ (3 + 2x2)′ = 16 (3 + 2x2)3 ⋅ х Пусть функция является обратной для функции . Если существует отличная от нуля производная функции по переменной x, то существует и производная обратной функции по переменной y. При этом 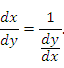
1 2 |
