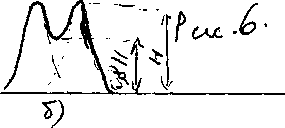фазовой зонной пластинкой. По сравнению с перекрывающей зоны амплитудной зонной пластинкой фазовая даст дополнительное увеличение амплитуда в два раза, а интенсивности света - в 4 раза.
Деление фронта волны Ф на зоны Френеля является относительным и зависит от расстояния до точки наблюдения М,
Пренебрегать дифракционными явлениями и рассматривать свет распространяющимся прямолинейно вдоль лучей, исходящих от источника, допустимо лишь, если размеры экрана велики по ср. с размерами зон Френеля. Чем короче l, тем меньше размеры этих зон и тем точнее можно пользоваться приближенными понятиями лучевой (геометрической) оптики. Т.к. для видимого света l = 0,4 - 0,8 мкм, то при наблюдении макроскопических тел этими приближениями можно пользоваться с достаточной точностью. Однако при уменьшении размеров тел начинают проявляться дифракционные явления.
Поставим на пути сферической световой волны непрозрачный экран с вырезанным в нем круглым отверстием радиуса г. Расположим экран так, чтобы перпендикуляр, опущенный из источника света S, попадал в центр отверстия. На продолжении этого перпендикуляра возьмем точку Р. Если расстояния а и b удовлетворяют соотношению (*), где m - целое число, то отверстие оставит открытым ровно m первых зон Френеля, построенных для точки Р. Из (*) число открытых зон Френеля определяется выражением
m = r02(1/а+1/b)/l. (6)
В соответствии с (3) амплитуда в точке Р будет равна
А = А1 -А2 +А3 –А4 +....±Аm (7)
Перед Аm берется знак «+», если m нечетное, и минус, если m - четное. Представив (7) в виде, аналогичном (4), и положив выражения в скобках равными нулю, получим
А = А1/2 + Аm /2 (m - нечетное),
А=А1/2 +Аm-1/2 – Аm (m - четное).
Амплитуды от двух соседних зон практически одинаковы. Поэтому (Аm-1/2) – Аm можно заменить через - Аm/2. В результате получится:
А = А1/2 ± Аm/2,
где знак «+» берется для нечетных m и минус - для четных.
Для малых m амплитуда Аm мало отличается от А1. Следовательно, при нечетных m амплитуда в точке Р будет приблизительно равна а1, при четных m - нулю.
А какая будет освещенность в других точках экрана? Вследствие симметричного расположения отверстия относительно прямой SР освещенность в разных точках экрана будет зависеть только от расстояния х от точки Р. Если смещаться по экрану в точку Р¢ и далее, то дифракционная картина будет иметь вид чередующихся светлых и темных концентрических колец. Если отверстие открывает лишь часть центральной зоны Френеля, на экране получается размытое светлое пятно; чередования светлых и темных колец в этом случае не возникает.
Аналогичная картина на экране получается и в рассмотренном выше случае, когда между источником света и экраном помещается непрозрачный круглый диск. Дифракционная картина на экране будет иметь вид чередующихся светлых и темных концентрических колец. В центре картины помещается светлое пятно.
16.ДИФРАКЦИЯ ФРАУНГОФЕРА НА ОДНОЙ ЩЕЛИ.
Пусть на бесконечно длинную щель падает плоская световая волна, рис.2.
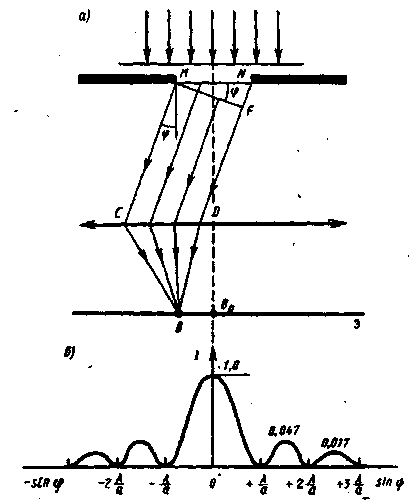
Рис.2.
Поместим за щелью собирательную линзу, а в фокальной плоскости линзы - экран. Волновая поверхность падающей волны, плоскость щели и экран параллельны друг другу. Поскольку щель бесконечна, картина, наблюдаемая в любой плоскости, перпендикулярной к щели, будет одинакова. Поэтому достаточно исследовать характер картины в одной такой плоскости.
Когда фронт волны дойдет до щели и займет положение MN, то все его точки являются новыми источниками волн, распространяющихся во все стороны вперед от щели. Рассмотрим волны, распространяющиеся от точек плоскости MN в направлении, составляющем некоторый угол j с первоначальным. Эти волны, проходя через линзу, сойдутся в некоторой точке B на экране, расположенном в фокальной плоскости линзы. Лучи, распространяющиеся от щели под различными углами, в результате интерференции дадут дифракционную картину.
Опустим из точки M перпендикуляр MF на направление выделенного пучка лучей. Тогда от плоскости MF и далее до фокальной плоскости Е параллельные лучи не меняют своей разности хода. Разность хода, определяющая условия интерференции, возникает лишь на пути от исходного фронта MN до плоскости MF и различна для разных лучей.
Для расчета интерференции всех этих лучей применим метод зон Френеля. Для этого мысленно разделим линию NF на ряд отрезков длиной l/2. На расстоянии NF = аsinj уложится
Z = (sinj)/(l/2) (1)
таких отрезков. Проводя из концов этих отрезков линии, параллельные MF, до встречи их с MN, мы разобьём фронт волны в щели на ряд полосок одинаковой ширины. Эти полоски и являются в данном случае зонами Френеля. Отсюда следует, что волны, идущие от каждых двух соседних зон Френеля, приходят в точку B в противоположной фазе и гасят др. др. Если число зон четное, z = 2k (где k - целое число, неравное нулю), то каждая пара соседних зон взаимно погасит др.др., так что при данном угле j на экране будет минимум освещенности. Углы j, соответствующие этим минимумам освещенности, находятся из условия:
аsinjmin = 2kl/2. (2)
В промежутках между минимумами наблюдаются максимумы освещенности при углах j, определяемых из условия
аsinjmax = (2k + 1)l/2. (3)
Для этих углов фронт MN разбивается на нечетное число зон Френеля z = 2k +1 и одна из зон остается непогашенной. Амплитуда в этом случае будет составлять долю 1/(2k+1), а интенсивность
1/(2k+1)2 от суммарной амплитуды, создаваемой всеми зонами фронта MN.
Центральный максимум будет расположен в точке О против центра щели. По обе стороны от него интенсивность будет спадать до первого минимума, а затем увеличиваться до следующего максимума, см. рисунок. На экране Е будут наблюдаться перемежающиеся светлые и темные полосы с постепенными переходами между ними. Центральная полоса будет наиболее яркой, а освещенность боковых максимумов будет убывать от центра к переферии.
Ширина и число этих полос будут зависеть от отношения l/а. Из (1) видно, что
zmax = a/(l/2). (4)
Если щель очень узкая, а«l, то вся поверхность MN является лишь небольшой частью одной зоны и колебания от всех её точек будут по любому направлению распространяться почти в одинаковой фазе. Условие минимума (2) не может быть выполнено даже для самого меньшего значения k = 1 и во всех точках экрана будет свет. Такая щель является практически точечным источником света, и волна от неё будет распространяется практически одинаково во всех направлениях.
Если щель очень широкая, а»l, то уже первый минимум будет соответствовать очень малому отклонению от прямолинейного распространения света под углом (j1)min = arcsinl/a »l/a <<1.(5)
Следующий минимум будет при угле (j2)min » 2l/a и т.д. В результате прохождения через такую широкую щель плоской волны на экране мы увидим геометрическое изображение щели, окаймлённое по краям тонкими перемеживающимися темными и светлыми полосками.
Чётко выраженные широкие дифракционные максимумы и минимумы будут наблюдаться лишь в промежуточном случае, когда ширина щели всего в несколько раз превышает длину волны и zmax порядка 3-5.
При освещении щели монохроматическим светом дифракционные максимумы для различных цветов разойдутся. Как видно из (3), чем меньше l, тем под меньшими углами расположены дифракционные максимумы.
В центр экрана лучи всех цветов приходят совместно - если щель освещалась белым светом, то изображение в центре также будет белым. Справа и слева от центрального максимума будут наблюдаться дифракционные спектры первого, второго и т. д. порядка, обращенные фиолетовым краем к центру, рис.3. Однако они настолько расплывчаты, что отчетливого разделения различных длин волн с помощью дифракции на одной щели получить невозможно.
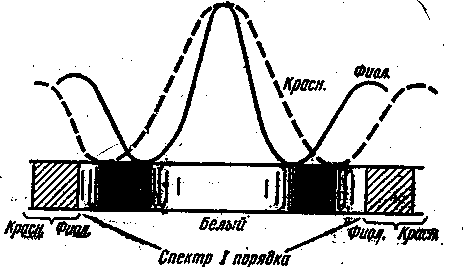
Рис.3.
17.ДИФРАКЦИОННАЯ РЕШЕТКА, ДИФРАКЦИОННЫЙ СПЕКТР. ДИСПЕРСИЯ И РАЗРЕШАЮЩАЯ СПОСОБНОСТЬ РЕШЁТКИ.
Для увеличения интенсивности и более четкого разделения цветов следует воспользоваться не одной щелью, а целой дифракционной решеткой, которая представляет собой ряд параллельных щелей одинаковой ширины а, разделённых между собой непрозрачными промежутками шириной b. Сумма а + b = 1(1) называется периодом или постоянной дифракционной решетки.
Конструктивно дифракционная решетка для видимого света изготавливается путем нанесения на прозрачную стеклянную пластинку с помощью алмазного резца делительной машины ряда тонких параллельных штрихов-канавок одинаковой ширины b на равных расстояниях а др. от др. Поверхность стекла внутри канавок становится матовой, и эти канавки являются непрозрачными промежутками, разделяющими участки с ненарушенной поверхностью - "
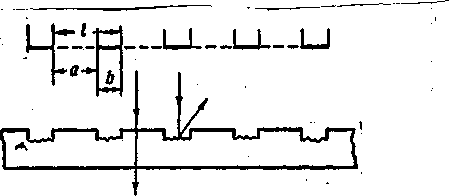
щели" решетки, Рис.1.
Рассмотрим плоскую монохроматическую волну, падающую на решетку, рис.2. Каждая из параллельных щелей решётки дает на экране Е дифракционную картину, показанную на рис.2 пунктиром. Линза L собирает параллельные лучи, идущие от всех щелей под углом Ф
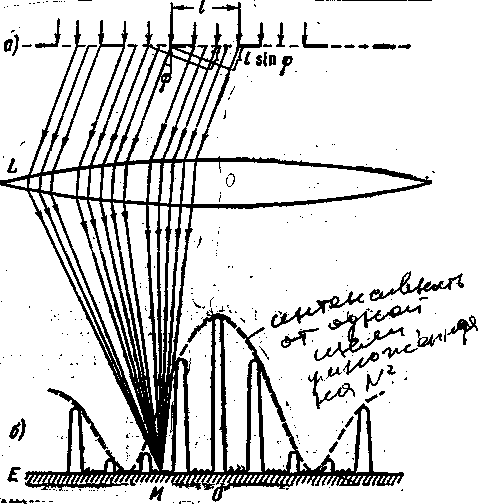
Pис.2.
к главной опт. оси, в одну и ту же точку М фокальной плоскости. При параллельности всех щелей дифракционной решётки и строгой одинаковости их размеров амплитуды колебаний, создаваемых в точке М каждой щелью в отдельности, будут одинаковы. Практически одинаковым будет и распределение вдоль экрана интенсивностей и амплитуд колебаний, приходящих от каждой щели. Дифракционная картина на решетке определяется как результат взаимной интерференции волн, идущих от всех щелей.
На центральной линии экрана (проходящей через главный фокус линзы О) лучи, идущие от всех щелей, сходятся без дополнительной разности хода, т.е. приходят в одинаковой фазе. При этом их амплитуды просто складываются, и в случае N одинаковых щелей амплитуда суммарного колебания будет в N раз, а интенсивность в N2 раз больше, чем в случае одной щели.
Лучи, идущие от разных щелей под углом j, отличным от нуля, сходятся в точке М, пройдя различные пути и имея различные фазы колебаний; они будут давать при интерференции более сложную картину. Рассмотрим две соседние щели. Из рис.2 видно, что лучи, идущие от соответственных точек обеих щелей (крайних, центральных, промежуточных), имеют одну и ту же разность хода D = l sinj (2) и приходят в т. М со сдвигом фазы y = 2p(l sinj)/l. Такой же точно сдвиг фазы y будет между колебаниями, приходящими от третьей щели и второй, четвертой и третьей, и т.д.
Резкое возрастание амплитуды результирующего колебания будет в тех случаях, когда амплитуды колебаний от всех щелей аi направлены одинаково, т.е. имеют сдвиг фазы, целый кратный от 2p, рис.3, что соответствует разности хода между соседними щелями D кратной четному числу полуволн:
lsinjk = 2kl /2 = kl, k = 0, ±1, ±2, ±3, .... (3)
Условие (3) характеризует положение главных максимумов дифракционной решетки. При углах jk, удовлетворяющих (3), А = NА1 и интенсивность дифракционной картины возрастает в К2 раз по ср. с дифракцией от одной щели.
С увеличением N возрастает четкость дифракционной картины - увеличивается интенсивность и уменьшается, ширина главных максимумов. Вследствие интерференции происходит, перераспределение энергии в пространстве, и эта энергия концентрируется, во все более узком интервале углов Djm.
Рис.3.
Подчеркнем, что хотя положение гл. максимумов решетки не зависит от числа щелей, наличие большого числа щелей очень существенно: 1)яркость каждой линии растет как N2, 2) ширина каждой линии убывает как 1/N. Тем самым увеличивается точность производимых измерений.
 Если на дифракционную решетку будет падать немонохроматический свет, то дифракционные максимумы, для лучей разного цвета пространственно разойдутся. Нулевой макс. (k=0) для всех длин волн будет совпадать при j = 0, но уже максимумы первого порядка (k=1) будут для фиолетовых лучей расположены ближе к центру, чем для красных. Между ними расположатся максимумы промежуточных цветов, и мы будем наблюдать дифракционный спектр первого порядка. Между нулевым и первым порядками расположена практически темная зона очень
слабых побочных максимумов. Такая же темная зона расположена между красным концом спектра первого порядка и фиолетовым краем спектра второго порядка, рис.4.
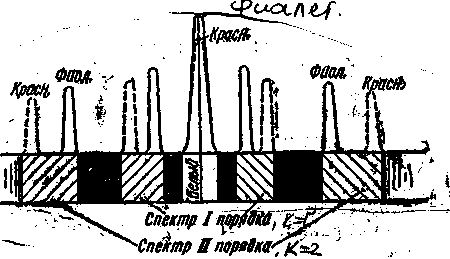
Благодаря узости дифракционных максимумов решетки различные цвета почти не накладываются др. на др. Это свойство дифракционной решетки используется для исследования спектрального состава света (определения длин волн и интенсивностей всех монохроматических компонентов), т.е. дифракционная решетка может быть использована как спектральный прибор (рис.5.). Спектр дифракционной решетки получается тем более четким, чем больше щелей N содержит решетка. Максимальное число наблюдаемых дифракционных спектров определяется из условия, чтобы sinjk <1, т.е. kmax£ l/l, (4)
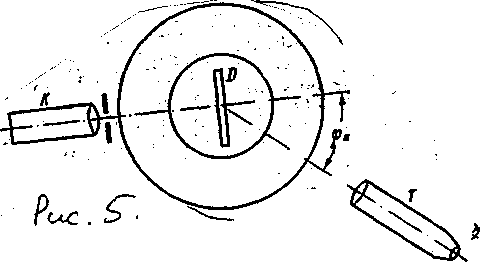
Из условия sinjk =kl/l(5) видно, что синусы углов в спектре данного порядка прямо пропорциональны длинам волн, т.е. дифракционные спектры, в отличие от призматических, всегда одинаковы и равномерны. Помещая дифракционную решетку D на столик гониометра ( рис.5) и освещая ее пучком параллельных лучей через щель коллиматора К, можно, измеряя угол jk, под которым видны данные лучи в зрительную трубу Т, точно найти их длину волны l.
Дифракционные решетки имеют обычно от 100 до 600 щелей на мм, т.е. период l=10-2 мкм. Лучшие решетки содержат до 1800 щелей на мм, при общей длине до нескольких см., так что общее число щелей достигает 105.
Отражательная решетка изготовляется процарапыванием параллельных штрихов на зеркальной поверхности. Её теория, по существу, не отличается от теории прозрачной решетки.
Для некоторых областей спектра стекло непрозрачно (например, для УФ-лучей). В этом случае нужно пользоваться кварцевой оптикой и отражательными решетками. Без линз можно обойтись, заменяя плоскую отражательную решетку вогнутой.
Основными характеристиками всякого спектрального прибора является его дисперсия и разрешающая сила. Дисперсия определяет угловое или линейное расстояние между двумя спектральными линиями, отличающимися по длине волны на единицу (например, на 1 ангстрем). Разрешающая сила определяет минимальную разность длин волн dl, при которой две линии воспринимаются в спектре раздельно.
Угловой дисперсией называется величина
D = dj/dl, (6)
где dj - угловое расстояние между спектр, линиями, отличающимися на dl (рис.6а). Можно показать, что
D = k/l, (7)
откуда следует, что угловая дисперсия обратно пропорциональна периоду решетки l. Чем выше порядок спектра k, тем больше дисперсия.
Дифракционная решетка
Рис.6а.
Линейной дисперсией называют величину Dлин = dl¢ /dl, (8) где dl¢ - линейное расстояние на экране или на фотопластинке между спектр. линиями, отличающимися по длине на dl. Линейная дисперсия связана с угловой дисперсией соотношением Dлин = fD, (9) где f - фокусное расстояние линзы, собирающей дифрагирующие лучи на экране. Приняв во внимание (7), запишем Dлин = fk/l, (10)
Разрешающей силой спектрального прибора называют безразмерную величину R = l/dl
где dl - минимальная разность длин волн двух спектральных линий, при которой эти линии воспринимаются раздельно.
Возможность разрешения (т.е. раздельного восприятия) двух близких спектральных линий зависит не только от расстояния между ними (которое определяется дисперсией прибора), но также и от ширины спектрального, максимума (рис. 6). Критерий Рэлея.
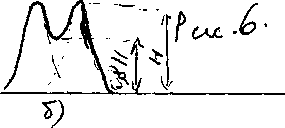
Разрешающая сила дифракционной решетки пропорциональна порядку спектра k и числу щелей N, т.е. Rдифр. реш. = kN.
Современные дифракционные решетки обладают довольно высокой разрешающей силой (до 2×105).
18.ДИФРАКЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ НА КРИСТАЛЛИЧЕСКОЙ РЕШЕТКЕ.
Напомню, что в 1895г Рентген обнаружил, что при электрическом разряде в вакуумной трубке возникает излучение, невидимое для глаза. Дальнейшие исследования показали, что эти лучи, названные рентгеновскими, возникают при бомбардировке вещества быстрыми электронами. В современных рентгеновских трубках мишенью, обстреливаемой электронами , является метал. пластинка -катод, расположенный под углом 45° к потоку электронов. Скорость электронов определяется величиной разности потенциалов между анодом и катодом.
Рентгеновские лучи, предст. собой жесткое электромагнитное излучение, также как и оптическое излучение, обладают волновыми свойствами. Мы уже знаем, что для того, чтобы обнаружить дифракцию, необходимо, чтобы размеры щелей и преград, образующих правильную решетку на пути волн, были не слишком велики по сравнению с длиной волны. Рентгеновские лучи обладают столь малой длиной волны, что на обычных дифракционных решетках для них дифракция не наблюдается.
Проделаем мысленно следующее. Поставим две дифр. решетки одну за другой так, чтобы их штрихи были взаимно перпендикулярными. Первая решетка даст например в горизонтальном направлении ряд максимумов, положения которых определяются условием
d1 sinj1 = ±m1l (m1 =0, 1,2,3,..,)(1)
Вторая решетка разобьет каждый из образовавшихся т.о. пучков на расположенные по вертикали максимумы, положения которых опр. условием
d2 sinj2 = ±m2l (m2 =0, 1,2,...).
В итоге дифракционная картина будет иметь вид правильно расположенных пятен.
Такая же дифракционная картина получится, если вместо двух разд. решеток взять одну прозрачную пластинку с нанесенными на нее двумя системами взаимно перпендикулярных штрихов. Подобная пластинка представляет собой двумерную периодическую структуру.
Дифракция наблюдается также на трехмерных структурах, т.е. пространственных образованиях, обнаруживающих периодичность по трем не лежащим в одной плоскости направлениям. Подобными структурами являются все кристаллические тела. Однако их период (» 10-10 м) слишком мал для того, чтобы можно было наблюдать дифракцию в видимом свете. В случае кристаллов условие d>l выполняется только для рентгеновских лучей. Впервые дифракция рентгеновских лучей от кристаллов наблюдалась в 1913 г. в опыте Лауэ, Фридриха и Книппинга.
Первые методы расчета дифракции от объемной решетки дал Лауэ.
Совершенно эквивалентные формулам Лауэ, но гораздо более удобные для анализа, формулы были даны независимо русским ученым Вульфом и английскими физиками У .Г. и У.Л .Брэггами. Метод, предложенный ими, состоит в следующем.
Проведем через узлы кристаллической решетки параллельные равноотстоящие плоскости (рис.1), которые мы будем называть
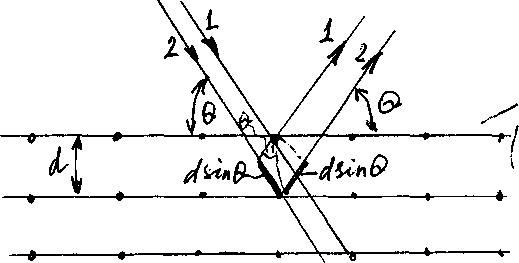
Рис.1.
атомными слоями. Если падающая на кристалл волна плоская, огибающая вторичных волн, порождаемых атомами,лежащими в таком слое, также будет представлять собой плоскость. Т.о., суммарное действие атомов, лежащих в одном слое, можно представить в виде плоской волны, отразившейся от усеянной атомами поверхности по обычному закону отражения.
Плоские вторичные волны, отразившиеся от разных атомных слоев, когерентны и будут интерферировать между собой подобно волнам, посылаемым в данном направлении различными щелями дифракционной решетки. При этом, как и в случае решетки, вторичные волны будут практически погашать друг друга во всех направлениях, кроме тех, для которых разность хода между соседними волнами является кратной l. Из рис.1 видно, что разность хода двух волн, отразившихся от двух соседних слоев, равна 2dsinQ, где d - период идентичности кристалла в направлении, перпендикулярном к рассматриваемым слоям, Q - угол, дополнительный к углу падения и называется углом скольжения падающих лучей. Следовательно, направления, в которых получаются дифракционные максимумы, определяется условием
2dsinQ = ± ml (m =1,2,...) (1)
Это соотношение называется формулой Вульфа –Брэггов.
Атомные слои в кристалле можно провести множеством способов. Каждая система слоев может дать дифракционный максимум, если для нее окажется выполнимым (1). Однако заметную интенсивность имеют лишь те максимумы, которые получаются за счет отражений от слоев, достаточно густо усеянных атомами. При произвольном направлении падения монохроматического рентгеновского излучения на кристалл дифракция не возникает. Чтобы ее наблюдать, надо, поворачивая кристалл, найти определенный угол скольжения. Дифракционная картина может быть получена и при произвольном положении кристалла, для чего нужно пользоваться рентгеновским излучением с непрерывным спектром. Тогда для таких условий опыта всегда найдутся длины волн l, удовлетворяющие условию (1).
Дифракция рентгеновских лучей от кристаллов находит два основных применения. Она используется для исследования спектрального состава рентгеновского излучения (рентгеновская спектроскопия) и для изучения структуры кристаллов (рентгеноструктурный анализ).
В методе структурного анализа пучок ренг. излучения направляется на кристалл. Для каждой системы слоев, достаточно густо усеянных атомами, находится в излучении длина волны, при которой выполняется условие (1). Поэтому на помещенной за кристаллом фотопластинке получается (после проявления) совокупность черных пятнышек, взаимное расположение которых отражает симметрию кристалла. По расстоянию между пятнышками и по их интенсивности удается найти размещение атомов в кристалле и расстояния между ними.
19.ПОЛЯРИЗАЦИЯ СВЕТА. ЕСТЕСТВЕННЫЙ И ПОЛЯРИЗОВАННЫЙ СВЕТ. СТЕПЕНЬ ПОЛЯРИЗАЦИИ. ЗАКОН МАЛЮСА.
Напомню, что поляризованным называется свет, в котором направления колебаний светового вектора Е упорядочены каким-либо образом. В естественном свете колебания разных направлений светового вектора Е быстро и беспорядочно сменяют друг друга.
Рассмотрим два взаимно перпендикулярных электрических колебания свершающихся вдоль осей х и у и отличающихся по фазе на d (Рис.1):
Еx = A1 coswt,
Еy = A2 cos(wt + d). (1)
Результирующая напряженность Е является векторной суммой Ех и Еу (рис.1), причем угол j равен
tg j = Е y /Е x = A2 cos(wt + d)/ A1 coswt, (2)
Рис.1.
Если разность фаз претерпевает случайные хаотические изменения, то и угол j, т.е. направление светового вектора Е, будет испытывать скачкообразные неупорядоченные изменения. В соответствии с этим естественный свет можно представить как наложение двух некогерентных электромагнитных волн, поляризованных во взаимно перпендикулярных плоскостях и имеющих одинаковую интенсивность. Такое представление намного упрощает рассмотрение прохождения естественного света через поляризационные устройства.
Допустим, что световые волны Ех и Еу когерентны, причем d равно нулю или p. Тогда согласно (2) tgj = ± А2/А1 = const.
Следовательно, результирующее колебание совершается в фиксированном направлении - волна оказывается плоско поляризованной.
В случае, когда А1 = А2 и d = ±p/2, tgj = ± tgwt т.к. (соs(wt±л/2) = ±sinwt). Отсюда вытекает, что плоскость колебаний поворачивается вокруг направления луча с угловой скоростью, равной частоте колебания w. В этом случае свет 6удет поляризованным по кругу.
В случае произвольного постоянного d в результате сложения двух взаимно перпендикулярных колебаний получим вектор Ё, конец которого движется по эллипсу (в частном случае, может получиться движение по прямой или по окружности), т.е. мы получаем в результате сложения таких волн эллиптически поляризованную световую волну. При разности фаз d=0 или d=p, эллипс вырождается в прямую и получается плоско поляризованный свет. При d = ±p/2 и равенстве амплитуд складываемых волн эллипс превращается в окружность - получается свет поляризованный по кругу.
В зависимости от направления вращения вектора Е различают правую и левую эллиптическую и круговую поляризацию. Если по отношению к направлению, противоположному направлению луча, вектор Е вращается по часовой стрелке, поляризация называется правой, в противоположном случае - левой.
Плоскость, в которой колеблется световой вектор в плоско поляризованной волне, называется плоскостью колебаний. Плоскостью поляризации называется не плоскость, в которой колеблется вектор Е, а перпендикулярная к ней плоскость.
Плоско поляризованный свет можно получить из естественного с помощью приборов, называемых поляризаторами. Эти приборы свободно пропускают колебания, параллельные плоскости, которую мы будем называть плоскостью поляризатора, и полностью или частично задерживают колебания, перпендикулярные к этой плоскости. Поляризатор, задерживающий перпендикулярные к его плоскости колебания только частично, называется несовершенным. Просто поляризатором мы будем для краткости называть идеальный поляризатор, полностью задерживающий колебания, перпендикулярные к его плоскости, и не ослабляющий колебаний, параллельных плоскости. Поляризатор представляет собой среду, структура и свойства которой в различных направлениях, перпендикулярных лучу, различны, т.е. эта среда анизотропна. Такими средами для света являются преимущественно кристаллические тела с невысокой степенью симметричности.
На выходе из несовершенного поляризатора получается свет, в котором колебания одного направления преобладают над колебаниями других направлений. Такой свет называется частично поляризованным. Его можно рассматривать как смесь естественного и плоско поляризованного. Частично поляризованный свет, как и естественный, можно представить в виде наложения двух некогерентных плоско поляризованных волн с взаимно перпендикулярными плоскостями колебаний. Отличие заключается в том, что в случае естественного света интенсивность этих волн одинакова, а в случае частично поляризованного - разная.
Если пропустить частично поляризованный свет через поляризатор, то при вращении прибора вокруг направления луча интенсивность прошедшего света будет изменяться в пределах от Imax до Imin, причем переход от одного из этих значений к другому будет совершаться при повороте на угол, равный p/2 (за один полный оборот два раза будет достигаться макс, и два раза мин. значение интенсивности). Величина
|
Скачать 2.4 Mb.