шпорки по физике-1. 1. основные харки мех. Движения. Прямолинейное и криволинейное движение материал. Точки. Скорость и ускорение. Механика

• Название: 1. основные харки мех. Движения. Прямолинейное и криволинейное движение материал. Точки. Скорость и ускорение. Механика
• Дата: 21.05.2022
• Размер: 2.4 Mb.
• Имя файла: шпорки по физике-1.doc
• Тип: Документы; #542230
• страница: 10 из 14

Движение заряженных частиц в электрическом и магнитном полях.

Полученное выше выражение для силы Лоренца позволяет установить ряд закономерностей движения заряженных частиц в магнитном поле, лежащих в основе устройства электронного микроскопа, масс-спектрографа и ускорителей заряженных частиц.

Рассмотрим движение заряженных частиц в однородном МП. При этом будем считать, что на частицы не действуют никакие электрические поля.

Начнем с простейшего случая - движения заряженной частицы вдоль линий индукции МП. При этом угол a между `U и `В равен 0 или p, поэтому F_л = 0, т.е. МП не действует на частицу. Она будет двигаться по инерции - равномерно и прямолинейно.

Пусть частица, имеющая заряд q, движется перпендикулярно линиям магнитной
индукции (a=p/2). Тогда F_л = |q|UВ. (3)

Следовательно, частица движется в плоскости, перпендикулярной вектору`В, причем сила Лоренца является центробежной силой, вычисляемой по формуле F_л = mU²/r , (4) где m -масса частицы, r- радиус кривизны ее траектории. Приравняв (3) и (4), найдем r = |m/q|U/В,

т.к. в однородном МП `В=соnst, а числовое значение скорости частицы не изменяется, то pадиус кривизны траектории частицы оказывается постоянным. Поэтому она будет двигаться по окружности плоскость которой ^`В, а радиус пропорционален отношению скорости частицы к произведению ее удельного заряда q/тна индукцию `В поля.

Поскольку направление силы`F_л и вызываемого ею отклонения заряженной частицы в МП зависят от знака ее заряда q, то если частица движется в плоскости чертежа слева направо, а МП направлено из-за чертежа его плоскости, то при q >0 частица отклонится вниз, а при q<0 - вверх. Т.о., по характеру отклонения частицы в МП можно судить о знаке ее заряда. Этим широко пользуются в исследованиях элементарных частиц. На этом принципе работают приборы масс-спектрометры, используемые для изучения химического состава различных проб (в том числе и геологических).

Частица движется по окружности радиуса г равномерно. Поэтому период обращения частицы

Т = 2pr/U = 2p | m/q | /В - период не зависит от скорости частицы.

Общий случай движения заряженной частицы в магнитном поле дает винтовую линию.

10.ЗАКОН ПОЛНОГО ТОКА, ВИХРЕВОЙ ХАРАКТЕР МАГНИТНОГО ПОЛЯ

Ранее мы получили, что

= 0.

Это соотношение свидетельствует о том, что электростатическое поле является потенциальным.

Магнитное_поле в отличие от электростатического - непотенциальное поле: циркуляция вектора `В магнитной индукции поля вдоль замкнутого контура, вообще говоря, не равна нулю и зависит от выбора контура. Такое поле в векторном анализе называется вихревым полем.

Рассмотрим МП бесконечного прямолинейного проводника с током I, находящемся в вакууме. Линии магнитной индукции этого поля представляют собой окружности, плоскости которых перпендикулярны проводнику, а центры лежат на его оси. Найдем циркуляцию вектора `В вдоль произвольной линии магнитной индукции - окружности ра­диуса r. . (1)

Вектор `В во всех точках линии численно равен

В = (m₀/4p)2I/r - по закону Б.-С.-Л. (2)

и направлен по касательной к этой линии, так что соs(`В,d`l) = 1. Следовательно,

(m₀/2p)(I/r) = m₀I (3)

Из (3) можно сделать два вывода: а)МП прямолинейного тока - вихревое поле, т.е. в нем циркуляция вектора `В вдоль линии магнитной индукции не равна нулю;

б) циркуляция вектора `В магнитной индукции поля прямолинейного тока в вакууме одинакова вдоль всех линий магнитной индукции и равна произведению магнитной постоянной на силу тока.

Мы видим, что в (3) не входит зависимость от размеров или формы контура, а можно и доказать, что (3) справедлива для любого замкнутого контура, охватывающего про­водник, независимо от формы этого контура.

При выводе (3) считалось, что обход контура происходит по часовой стрелке, При противоположном направлении обхода контура вместо (3) получается

- m₀I. (3')

Если в этом случае ток I считать отрицательным, то (3') эквивалентна (3). Поэтому в дальнейшем мы будем пользоваться (3), полагая в ней I>0, если направление тока в проводнике соответствует (по правилу буравчика) направлению обхода контура, и считая I<0 в противном случае.

Если замкнутый контур не охватывает проводника с током, тогда

0, (4).

т.е. циркуляция вектора магнитной индукции поля прямолинейного проводника с то­ком вдоль замкнутого контура, не охватывающего этого проводника, равна нулю.

Можно доказать, что (3) и (4) универсальны, т.е. справедливы для МП проводника с током любой формы и любых размеров, а не только для МП бесконечного прямолинейного проводника с током.

В общем случае, когда МП создается системой из n проводников с током I₁,...I_n ,

, -закон полного тока для МП в вакууме.

где n- число проводников, охватываемых контуром.

Закон полного тока для МП в вакууме: циркуляция вдоль замкнутого контура вектора индукции МП в вакууме равна произведению магнитной постоянной на алг. сумму токов, охватываемых этим контуром.
11.ПОТОК ВЕКТОРА МАГНИТНОЙ ИНДУКЦИИ. ТЕОРЕМА ОСТРОГРАДСКОГО-ГАУССА.

Потоком вектора магнитной индукции или магнитным потоком сквозь малую пло­щадку dS называется физическая величина, равная произведению этой площадки и проекции В_n вектора`В на направление нормали `n к площадке dS:

dФ = В_ndS = В dS соs(`В,`n) = `В ×d`S ,

где d`S = `n dS - вектор площадки dS. Интегрируя это выражение по S, получим

Ф= , (1)

где Ф - магнитный поток сквозь произвольную поверхность S.

При вычислении этого интеграла векторы `n нормалей к площадкам dS нужно направлять в одну и туже сторону по отношению к поверхности S. Например, если S -замкнутая поверхность, то векторы `n должны быть либо все внешними, либо все внутренними.

Е 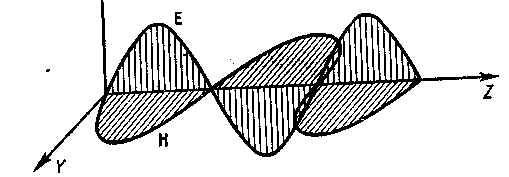сли МП однородное, а S - плоская и S ^`В, то В_n =В = соnst и Ф = BS. (2)

За единицу магнитного потока принимается магнитный поток сквозь плоскую по­верхность единичной площади, расположенную перпендикулярно однородному МП, индукция которого равна единице. Единица магнитного, потока в СИ называется вебером (Вб):

1Вб=1(В×с/м²)×1м² = 1В×с,

В электродинамике доказывается следующая теорема Остроградского-Гаусса для МП: магнитный поток сквозь произвольную замкнутую поверхность равен нулю:

(3)

Эта теорема является математическим следствием отсутствия в природе магнитных «зарядов" на которых могли бы начинаться и заканчиваться линии магнитной индукции.
12.СВЕТОВЫЕ ВОЛНЫ

Свет представляет собой сложное явление: в одних случаях он ведет себя как электромагнитная волна, в других - как поток особых частиц (фотонов). Длительный путь развития учения о свете привел к современным представлениям о двойственной корпускулярно-волновой природе света. Мы с Вами вначале рассмотрим круг явлений, в основе которых лежит волновая природа света.

Теоретические исследования Максвелла о распространении электромагнитных волн, экспериментальные измерения скорости их распространения в пустоте, оказавшейся равной скорости распространения света в пустоте, и другие исследования позволили выдвинуть предположение о чисто электромагнитной природе света.

Электромагнитная теория света явилась существенным шагом вперед в понимании природы оптических явлений. Свет оказался частным случаем электромагнитных волн с длиной волны от l = 400 нм (фиолетовый) до l=7бО нм (красный). Только этот интервал длин электромагнитных волн оказывает непосредственное воздействие на наш глаз и является собственно светом. Однако и более коротковолновое (l<400 нм -ультрафиолетовое) и более длинноволновое излучение (l>760 нм -инфракрасное) имеют качественно одну и ту же электромагнитную природу и отличаются лишь методами их возбуждения и обнаружения.

В электромагнитной волне колеблются векторы Е и Н, причем Е^Н (рис.1). Как показывает опыт, физиологическое, фотохимическое, фотоэлектрическое и другие действия света вызываются колебаниями вектора напряженности электрического поля Е, о котором говорят поэтому как о световом векторе. О магнитном векторе Н световой волны мы упоминать почти не будем.
Рис.1. Взаимное расположение векторов Е и Н в световой волне.

Модуль амплитуды светового вектора мы будем обозначать А (иногда Е_м). Соответственно изменение во времени и пространстве проекции светового вектора на направление, вдоль которого он колеблется, будет описываться уравнением

Е = Асоs(wt – kr + a) – уравнение световой волны (1)

где k - волновое число (k = 2p/l), r- расстояние, отсчитываемое вдоль направления распространения световой волны. Для плоской световой волны, распространяющейся в непоглощающей среде, А = const, для сферической волны А убывает как 1/r и т.д.

Отношение скорости распространения световой волны в вакууме (с) к ее скорости в некоторой среде V называется абсолютным показателем преломления этой среды и обозначается буквой n. Таким образом, n = с/ V. (2)

Из электромагнитной теории следует, что n = Öem, где e и m - диэлектрическая и магнитная проницаемости среды. Для подавляющего большинства прозрачных веществ m практически не отличается от единицы. Поэтому можно считать, что n = Öe. Эта формула связывает оптические и электрические свойства вещества. В эту формулу надо подставлять e, полученное для соответствующей частоты, так как n зависит от частоты (длины волны) света.

Значения показателя преломления характеризуют оптическую плотность cреды. Среда с большим n называется оптически более плотной, чем cреда с меньшим n, и наоборот.

Как уже отмечалось, длины волн видимого света l = 400 - 760 нм. Эти значения относятся к световым волнам в вакууме, В веществе длины световых волн будут иными. В случае колебаний частоты n длина волны в вакууме равна l₀ = c/n. В среде, в которой фазовая скорость световой волны V = с/n, длина волны имеет значение

l = V/n = c/nn =l₀/n.

Т.о. длина световой волны в среде с показателем преломления n связана с длиной волны в вакууме соотношением l = l₀ /n.

Частоты видимых световых волн лежат в пределах n = (3,9-: 7,5) 10¹⁴ Гц.

Частота изменений плотности потока энергии, переносимой волной, будет еще больше (она равна 2n). Уследить за столь быстрыми изменениями потока энергии не могут ни глаз, ни приборы, вследствие чего они регистрируют усредненный по времени поток.

Модуль среднего по времени значения плотности потока энергии, переносимой световой волной носит название