МЕХАНИКА(1-19). 1. Основные понятия кинематики материальной точки. Описание движения в декартовых координатах. Скорость, нормальное и тангенциальное ускорение при криволинейном движении. Движение материальной точки по окружности. Равномерное и равнопеременное вращение

• Название: 1. Основные понятия кинематики материальной точки. Описание движения в декартовых координатах. Скорость, нормальное и тангенциальное ускорение при криволинейном движении. Движение материальной точки по окружности. Равномерное и равнопеременное вращение
• Анкор: МЕХАНИКА(1-19).docx
• Дата: 07.02.2017
• Размер: 1 Mb.
• Имя файла: МЕХАНИКА(1-19).docx
• Тип: Документы; #2407
• страница: 4 из 4

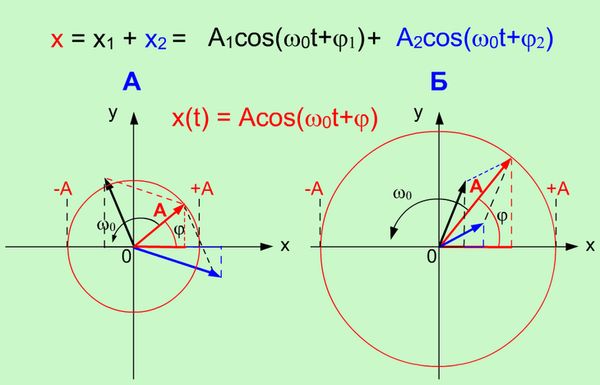
13.Гироскоп.Вывод формулы частоты прецессии гироскопа.

Гироскоп - устройство, способное реагировать на изменение углов ориентации тела, на котором оно установлено в ИнСиОт. Вывод: M=L/t (М-момент силы);
(am / JΩ) g; - маховик гироскопа будет совершать медленное вращение (прецессию) в горизонтальной плоскостиΩ L=JΩ( Ω– угловая частота); М = [a, F]; F=mg; L/t = [Ω, L]; [ωo, JΩ] = - [mg, a];

14.дифференциальное уравнение гармонических колебаний и его решение. Основные характеристики гармонических колебаний. Векторное изображение колебаний. Гармонические колебания груза на пружине, математического и физического маятников. Энергия гармонических колебаний(на примере пружинного маятника) Графики зависимости смещения, скорости, ускорения, кинетической и потенциальной энергии колебаний от времени.

(d^2)s/d(t^2)+ωs=0; (d^2)s/d(t^2)= -A (ω^2)(sin^2 )(ωt+φ); ds/dt= Acosx(ωt+φ); s(t)=Asinx(ωt+φ)-уравнение гармонических колебаний. Колебания вдоль оси х. Бывают свободные и вынужденные.
Для расчета Гарм.колеб обычно рассматривают плоскость векторного изображения как комплексную плоскость с вращающемся вектором А, c соотношением z=A(cos ωt+isin ωt)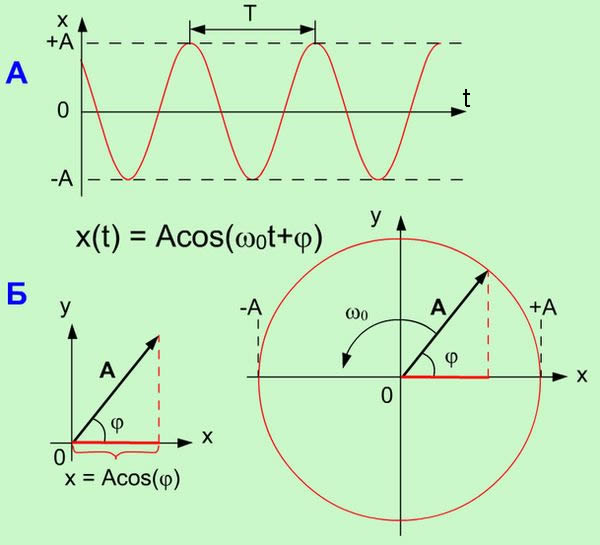



15.Сложение двух гармонических колебаний одинакового направления и частоты. Геометрическая интерпретация.

При сложении двух гармонических колебаний одинакового направления и частоты, результирующее смещение будет суммой () смещений  и , которые запишутся следующими выражениями:

, ,
Сумма двух гармонических колебаний также будет гармоническим колебанием той же круговой частоты: 
 =  .
Значения амплитуды А и начальной фазы φ этого гармонического колебания будет зависеть от амплитуд исходных колебаний и их начальных фаз (Рис. 1.2).

Рисунок 1.2. Сложение двух гармонических колебаний одинакового направления и частоты

На рисунке 1.2. приведено два примера А и В сложения гармонических колебаний с использованием метода векторных диаграмм. Из векторных диаграмм видно, что направление (начальная фаза φ) и длина А вектора амплитуды суммарного гармонического колебания зависит, как от направления (от начальных фаз), так и от длины векторов амплитуд исходных гармонических колебаний. 
Если угол (разность фаз: Δφ = φ1 - φ2) между векторами А1 и А2 равен 0, то исходные колебания находятся в фазе и суммарная амплитуда (А =А1 +А2) будет максимальна. Если угол (разность фаз: Δφ = φ1 - φ2) между векторами А1 и А2 равен - π или π, то исходные колебания находятся в противофазе и суммарная амплитуда (А = А1 -А2) будет минимальна.

16.Дифференциальное уравнение затухающих колебаний и его решение. Основные характеристики затухающих колебаний. Логарифмический декремент затухания. Апериодический процесс.

будем считать, что наряду с упругой или квазиупругой силой F_y в системе действует сила трения, пропорциональная скорости и направленная противоположно ей: F_тр = . Тогда учет влияния этих двух сил на характер движения приводит к следующему дифференциальному уравнению:

 8)

Разделив левую и правую части уравнения (8) на m ,обозначив r/m = 2bи сохранив обозначение к/m= w₀², приведем это уравнение к виду:

 (9)

Решение этого уравнения имеет вид:

 (10)

Формула (10) представляет собой смещение при затухающем колебании как функцию времени и параметров системы bи w. Коэффициент b = r/2mимеет смысл коэффициента затухания. Из формулы (10) видно, что в затухающих колебаниях амплитуда уменьшается со временем. Причем, колебания затухают тем быстрее, чем больше коэффициент затухания b. По сравнению с гармоническими колебаниями уменьшается также и циклическая частота колебаний w. Это уменьшение зависит от коэффициента затухания. Оказывается, что

 (11)

Колебательный процесс может происходить лишь при условии: (w₀²- b²)>0, когда частота wв формуле (11) является действительной величиной . Если же затухание в системе слишком велико (w₀< b ) , то под корнем в формуле (11) оказывается отрицательная величина, - в этом случае движение не имеет периодического характера.

Графически затухающее колебания представлено на рис.2, где сплошной линией показана зависимость смещения от времени, а пунктирной - экспоненциальный закон убывания амплитуды.

что быстрота убывания амплитуды затухающих колебаний характеризуется коэффициентом затухания b, который зависит от параметров системы. На практике затухание колебаний удобнее характеризовать декрементом затухания d, представляющим собой отношение двух последовательных амплитуд, разделенных периодом колебаний Т(см. рис.2) :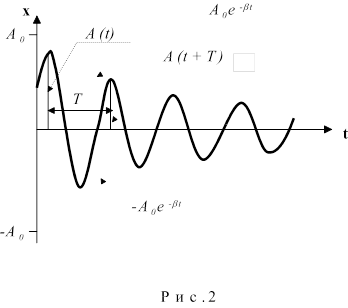

 

 



 

Натуральный логарифм этого отношения, называемыйлогарифмическим декрементомзатуханияl, весьма просто связан с коэффициентом затухания и периодом: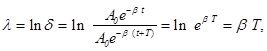

 или l = bT .(12)

Удобство использования логарифмического декремента затухания lдля характеристики затухающих колебаний заключается в простоте его экспериментального определения. Если затухающие колебания зарегистрированы в виде соответствующего графика (см.рис.2), то необходимо в любых единицах измерить две амплитуды колебаний, разделенные интервалом времени, равным периоду, и найти натуральный логарифм их отношения. Определив таким образом величину lи зная период Т, легко найти и коэффициент затухания b .

Для характеристики качества колебательной системы вводится ряд параметров:

 - время релаксации затухающих колебаний (за амплитуда уменьшается в e раз).   

   - логарифмический декремент затухания; N - число колебаний, в течение которых амплитуда уменьшается в eраз. Соответственно, exp() - просто декремент затухания.

   - добротность колебательной системы; W(t) - энергия (полная) колебательной системы в момент времениt.

17.Дифференциальное уравнение вынужденных колебаний и его решение. Резонанс. Резонансные кривые.

Предположим, что эта вынуждающая сила F_вдействует периодически с круговой частотой w_ви зависит от времени по закону : F_в= F_о sin w_вt, где F_о- амплитуда вынуждающей силы.

Для этого случая дифференциальное уравнение (второй закон Ньютона) имеет вид:

 (13)

Сохраняя обозначения к / m = w₀² , r / m = 2b , и обозначивF₀/m = f₀приведем уравнение (13) к виду:

 (14)

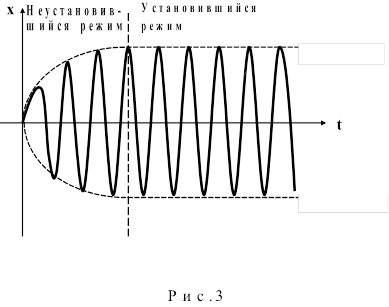
Решение этого уравнения представляет некоторую функцию, которая графически представлена на рис. 3. Это решение состоит из двух частей. Одна из них соответствует неустановившемуся режиму колебаний, когда их амплитуда зависит от времени. Вторая часть описывает установившийся режим колебаний.

В установившемся режиме вынужденных колебаний смещение хподчиняется гармоническому закону и происходит с частотой, равной частоте действия вынуждающей силы:

х = А sin (w_вt + j_o) .(15)

Установившаяся амплитуда Авынужденных колебаний, зависит от параметров системы (частоты собственных колебаний w₀ и коэффициента затухания b ) и от характеристик вынуждающей силы (f₀ и w_в): А = f (w₀,b , f₀,w_в). (15):

 (16)

 (17)

Из (16) следует, что А_mахпри определенном соотношении между величинами w₀,w_ви b .

Минимум знаменателя в формуле (16) достигается при условии:

 (18)

 

То есть, амплитуда вынужденных колебаний максимальна, если частота действия вынуждающей силы определяется формулой (18). Явление резкого возрастания амплитуды вынужденных колебаний при частоте действия вынуждающей силы, определяемой формулой (16), называется резонансом.

Если бы затухание в системе отсутствовало (b = 0), то резонанс наступал бы при условии (w₀= w_в)и при этом амплитуда достигала бы бесконечно большого значения.

18.Основные характеристики механических волн в упругой среде. Продольные и поперечные волны. Уравнение плоской гармонической волны. Закон Гука . Плотность потенциальной энергии упругой деформации. Энергия упругой волны . Плотность потока энергии волны.

19.Постулаты специальной теории относительности. Преобразование Лоренца. Относительность интервала времени. Относительность одновременности. Собственное время. Относительность длины отрезка. Преобразование для скоростей. Импульс и энергия в теории относительности. Связь энергии и импульса.