МЕХАНИКА(1-19). 1. Основные понятия кинематики материальной точки. Описание движения в декартовых координатах. Скорость, нормальное и тангенциальное ускорение при криволинейном движении. Движение материальной точки по окружности. Равномерное и равнопеременное вращение
 Скачать 1 Mb. Скачать 1 Mb.
|
|
Момент инерции Моментом инерции системы (тела) относительно данной оси называется физическая величина, равная сумме произведений масс n материальных точек системы на квадраты их расстояний до рассматриваемой оси: В случае непрерывного распределения масс эта сумма сводится к интегралу где интегрирование производится по всему объему тела. При этом величина r в есть функция положения точки с координатами х, у, z. В качестве примера будем искать момент инерции однородного сплошного цилиндра высотой h и радиусом R относительно его геометрической оси (рис. 1). 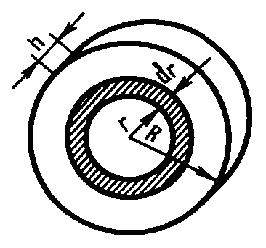 Рис.1 Разобьем цилиндр на отдельные полые концентрические цилиндры бесконечно малой толщины dr с внутренним радиусом r и внешним r+dr. Момент инерции отдельного полого цилиндра dJ=r2dm (так как dr< но так как πR2h - объем цилиндра, то его масса m=πR2hρ, а момент инерции Если мы знаем момент инерции тела относительно оси, проходящей через его центр масс, то мы можем найти и момент инерции относительно любой другой параллельной этой оси, который можно найти с помощью теоремы Гюйгенса-Штейнера: момент инерции тела J относительно произвольной оси равен моменту его инерции Jcотносительно параллельной оси, проходящей через центр масс С тела, сложенному с произведением массы m тела на квадрат расстояния а между осями: Приведем значения моментов инерции (табл. 1) для некоторых тел (тела считаются однородными, m - масса тела).  11.Основные уравнения динамики вращательного движения твердого тела. Основной закон динамики вращательного движения можно получить из второго закона Ньютона для поступательного движения твердого тела где F – сила, приложенная к телу массой m; а – линейное ускорение тела. Если к твердому телу массой m в точке А (рис. 5) приложить силу F, то в результате жесткой связи между всеми материальными точками тела все они получат угловое ускорение где где mi – масса i-й точки; Умножая левую и правую части уравнения (1.7) на ri, получают где Плечом силы называют кратчайшее расстояние от оси вращения “ОО” (рис. 5) до линии действия силы 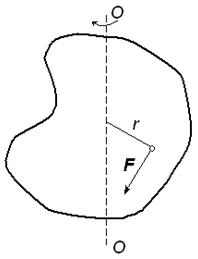 Рис. 5. Твердое тело, вращающееся под действием силы F около оси “ОО” Выражение (1.8) можно записать так: Просуммируем левую и правую части (1.9) по всем точкам тела: 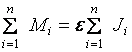 . .Обозначим 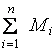 через М, а через М, а Уравнение (1.10) – основной закон динамики вращательного движения твердого тела. Величина 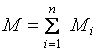 – геометрическая сумма всех моментов сил, то есть момент силы F, сообщающий всем точкам тела ускорение – геометрическая сумма всех моментов сил, то есть момент силы F, сообщающий всем точкам тела ускорение 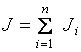 – алгебраическая сумма моментов инерции всех точек тела. Закон формулируется так: «Момент силы, действующий на вращающееся тело, равен произведению момента инерции тела на угловое ускорение». – алгебраическая сумма моментов инерции всех точек тела. Закон формулируется так: «Момент силы, действующий на вращающееся тело, равен произведению момента инерции тела на угловое ускорение».Мгновенное значение углового ускорения 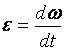 , (1.11) , (1.11)где Если в выражение основного закона (1.10) поставить значение мгновенного ускорения (1.11), то 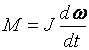 или или где Поэтому основной закон динамики вращательного движения твердого тела формулируется так: “Импульс момента силы 12. кинетическая энергия вращающегося твердого тела. Работа сил при вращательном движении тела. Кинетическая энергия твердого тела при плоском движении. Вращательное движение твёрдого тела.
Плоское движение твёрдого тела
Кинетическая энергия вращающегося твёрдого тела. Работа момента сил
Плоское движение твёрдого тела
Вращение твёрдого тела. Кинетическая энергия вращающегося тела. Поступательное движение Вращательное движение v – линейная скорость ω – угловая скорость a = dv/dt – линейное ускорение ε = dω/dt – угловое ускорение m – масса I – момент инерции p = mv – импульс Lz = Iωz – момент импульса F – сила M – момент силы dp/dt = ma = mdv/dt = F dL/dt = Iε = Idω/dt = M K = mv2/2 = p2/2m K = Iω2/2 = Lz2/2I dA = Fds dA = Mdφ Кинетическая энергия при плоском движении Плоским (плоскопараллельным) называется такое движение, при котором все точки тела движутся в параллельных плоскостях. Представим плоское движение тела как поступательное движение со скоростью В этом случае скорость i-той материальной точки тела определяется формулой Кинетическая энергия i- той материальной точки равна или Просуммировав по всем материальным точкам, получим 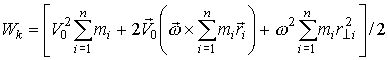 или где М -полная масса тела, Если в качестве точки О взять центр масс тела С, то Таким образом, если разбить плоское движение тела на поступательное со скоростью центра масс Vc и вращательное с угловой скоростью w вокруг оси, проходящей через центр масс тела, то кинетическая энергия распадается на два независимых слагаемых, одно из которых определяется только скоростью центра масс Vc, а другое - угловой скоростью w. Из (13) следует, что при вращении тела относительно оси z, проходящей через центр масс С, его кинетическая энергия |
