1 вопрос. Динамика точки. Основные понятия и определения

Название	1 вопрос. Динамика точки. Основные понятия и определения
Дата	19.06.2018
Размер	1.54 Mb.
Формат файла
Имя файла	teor_mekh_ekz.docx
Тип	Документы #47316
страница	1 из 11

1 2 3 4 5 6 7 8 9 10 11

_{1 вопрос}_._{Динамика точки. Основные понятия и определения…}

_{В разделе кинематики исследовалось движение тел без учета причин, обеспечивающих это движение. Рассматривалось движение, заданное каким-либо способом и определялись траектории, скорости и ускорения точек этого тела.В разделе динамики решается более сложная и важная задача. Определяется движение тела под действием сил приложенных к нему, с учетом внешних и внутренних условий, влияющих на это движение, включая самих материальных тел.}

_{Динамикой называется раздел механики, в котором изучаются законы движения материальных тел под действием сил.}

_{Понятие о силе, как о величине, характеризующей меру механического взаимодействия материальных тел, было введено в статике. Но при этом в статике мы, по существу, считали все силы постоянными. Между тем, на движущееся тело наряду с постоянными силами (постоянной, например, можно считать силу тяжести) действуют обычно силы переменные, модули и направления которых при движении тела изменяются.}

_Сила_{– векторная физическая величина, характеризующая действие одного тела на другое, в результате чего у тела изменяется скорость, то есть}_{появляется ускорение}_{, или происходит}_{деформация}_{тела, либо имеет место и то, и другое. В том случае, когда тело при взаимодействии получает ускорение, говорят о}_{динамическом}_{проявлении сил. В том случае, когда тело при взаимодействии деформируется, говорят о}_{статическом}_{проявлении сил.}_{– векторная величина.}

_{Как показывает опыт, переменные силы могут определенным образом зависеть}_{от времени, от положения тела}_и_{от его скорости.}_{В частности, от времени зависит сила тяги электровоза при постепенном выключении или включении реостата; от положения тела зависит сила упругости пружины; от скорости движения зависят силы сопротивления среды (воды, воздуха).}

_{К понятию об инертности тел мы приходим, сравнивая результаты действия одной и той же силы на разные материальные тела. Опыт показывает, что если одну и ту же силу приложить к двум разным, свободным от других воздействий покоящимся телам, то в общем случае по истечении одного и того же промежутка времени эти тела пройдут разные расстояния и будут иметь разные скорости.}

_{Инертность}_{и представляет собой}_{свойство материальных тел быстрее или медленнее изменять скорость своего движения под действием приложенных сил.}_{Если, например, при действии одинаковых сил изменение скорости первого тела происходит медленнее, чем второго, то говорят, что первое тело является более инертным, и наоборот.}

_{Количественной мерой инертности данного тела является физическая величина, называемая}_{массой тела.}_{В механике масса}_т_{рассматривается как величина скалярная, положительная и постоянная для каждого данного тела.}

_{За единицу массы принят эталон – сплав платины и иридия, хранящийся в палате мер и весов в Париже: [}_m_{]=кг. Масса–величина аддитивная}

_{и скалярная.}

_{В общем случае движение тела зависит не только от его суммарной массы и приложенных сил; характер движения может еще зависеть от формы тела, точнее от взаимного расположения образующих его частиц (т.е. от распределения масс).}

_{Чтобы при первоначальном изучении динамики иметь возможность отвлечься от учета влияния формы тел (распределения масс), вводится понятие о материальной точке.}

_Под_{материальной точкой}_{понимают материальное тело столь малых размеров, что различием в движении отдельных его точек можно пренебречь и положение которого можно определить координатами одной из его точек.}

_{Практически данное тело можно рассматривать как материальную точку в тех случаях, когда расстояния, проходимые точками тела при его движении, очень велики по сравнению с размерами самого тела. Кроме того, как будет показано в динамике системы}_{поступательно}_{движущееся тело можно всегда рассматривать как материальную точку с массой, равной массе всего тела.}

_{При вращательном движении тела точки могут двигаться неодинаково, в этом случае некоторые положения динамики можно применять только к отдельным точкам, а материальный объект рассматривать как совокупность материальных точек.}

_{Поэтому}_п_{ри изучении динамики выделяют два основных раздела: "Динамика материальной точки" и "Динамика материальной системы", из которых первый предваряет второй.}

_{Время в классической механике не связано с пространством и движением материальных объектов. Во всех системах отсчета движущихся друг относительно друга оно протекает одинаково.}

_{……………………………………………………………………………………………………………………………………………………………………………………………..2 вопрос}

_{Законы динамики}

_{В основе динамики лежат законы, установленные путем обобщения результатов целого ряда опытов и наблюдений над движением тел и проверенные обширной общественно-исторической практикой человечества. Систематически эти законы были впервые изложены И. Ньютоном.}

_{Первый закон (закон инерции)}_{, открытый Галилеем, гласит:}_{существуют такие системы отсчета, относительно которых тело покоится или движется прямолинейно и равномерно, если на него не действуют другие тела или действие этих тел компенсировано.}

_{или в другой формулировке}

_{если сумма действующих на тело сил равна нулю, то тело движется равномерно и прямолинейно или находится в покое.}

_{Движение, совершаемое точкой при отсутствии сил, называется движением}_{по инерции.}

_{Закон инерции отражает одно из основных свойств материи - пребывать неизменно в движении и устанавливает для материальных тел эквивалентность состояний покоя и движения по инерции. Из него следует, что если}_F_=0,_{то точка покоится или движется с постоянной по модулю и направлению скоростью}₍₌_const_{); ускорение точки при этом равно нулю:}_{= 0); если же движение точки не является равномерным и прямолинейным, то на точку действует сила.}

_{Система отсчета, по отношению к которой выполняется закон инерции, называется}_{инерциальной системой отсчета}_{(иногда ее условно называют неподвижной). По данным опыта для нашей Солнечной системы инерциальной является система отсчета, начало которой находится в центре Солнца, а оси направлены на так называемые неподвижные звезды. При решении большинства технических задач инерциальной, с достаточной для практики точностью, можно считать систему отсчета, жестко связанную с Землей.}

_{Системы отсчета, в которых не выполняется первый закон Ньютона, называются}_{неинерциальными}_._{Неинерциальными будут системы, движущиеся с ускорением, или вращающиеся.}

_{Второй закон (основной закон динамики)}_{гласит:}_{произведение массы точки на ускорение, которое она получает под действием данной силы, равно по модулю этой силе, а направление ускорения совпадает с направлением силы (рис.1).}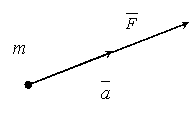

_Рис.1

_{Математически этот закон выражается векторным равенством}_.

_{При этом между модулями ускорения и силы имеет место зависимость}_ma₌_F_.

_{Второй закон динамики, как и первый, имеет место только по отношению к инерциальной системе отсчета.}_{Из этого закона непосредственно видно, что мерой инертности материальной точки является ее масса, так как две разные точки при действии одной и той же силы получают одинаковые ускорения только тогда, когда будут равны их массы; если же массы будут разные, то точка, масса которой больше (т. е. более инертная), получит меньшее ускорение, и наоборот.}

_{Известно, что вес тела и ускорение его свободного падения пустоте существенно зависят от места земной поверхности. В данной точке земли ускорение свободного падения всех тел одинаково и обозначается буквой}_g_{. Экспериментально установлено, что отношение веса}_Р_{тела к ускорению его свободного падения g есть постоянная величина, не зависящая от места наблюдения. Это отношение m = P/g также определяет массу тела. Таким образом, различают тяжелую массу}_m₁₌_P/g_{и инертную массу}_m₂_{= F/a. В классической механике считается, что}_m₁₌_m₂₌_m_.

_{Если на точку действует одновременно несколько сил, то они, как известно, будут эквивалентны одной силе, т.е. равнодействующей}_,_{равной геометрической сумме этих сил. Уравнение, выражающее основной закон динамики, принимает в этом случае вид}

_или_.

_{Существует и более}_{формулировка второго закона Ньютона: скорость изменения импульса материальной точки равно действующей на нее силе:}_{. Данное выражение называется уравнением движения материальной точки.}

_{В общем случае сила, действующая на тело, изменяется со временем и по величине, и по направлению. Но в течение элементарного промежутка времени}_dt_{мы можем считать, что}₌_const_{. Векторная величина}_{, равная}_{, называется}_{элементарным импульсом (силы).}

_{Второй закон Ньютона в дифференциальной форме:}

_{в проекциях на оси:}

_{Из второго закона также получим размерность силы: 1Н=1 кг∙1 м/с}₂_.

_{Третий закон (закон равенства действия и противодействия)}_{устанавливает характер механического взаимодействия между материальными телами. Для двух материальных точек он гласит:}_{две материальные точки действуют друг на друга с силами, равными по модулю и направленными вдоль прямой, соединяющей эти точки, в противоположные стороны (рис.2).}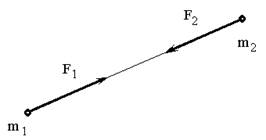

http://www.teoretmeh.ru/dinamika1.files/image220.jpg

_Рис.2

_{Заметим, что силы взаимодействия между свободными материальными точками (или телами), как приложенные к разным объектам, не образуют уравновешенной системы.}

_{Проведём небольшой эксперимент. Попробуем перемещать тяжёлое тело по некоторой криволинейной траектории. Сразу обнаружим, что тело сопротивляется изменению направления движения, изменению скорости. Возникает сила со стороны тела, противодействующая силе}_{, той, которую мы прикладываем к нему.}

_{Эту силу, с которой материальная точка сопротивляется изменению своего движения, будем называть}_{силой инерции}_{этой точки -}_{. По третьему закону она равна и противоположна действующей на точку силе}_,_{. Но на основании второй аксиомы}_{. Поэтому}_.

_{Итак, сила инерции материальной точки по величине равна произведению её массы на ускорение}

_F_ин=_m_a_.

_{И направлена эта сила инерции в сторону противоположную вектору ускорения.}

_{Например, при движении точки по кривой линии ускорение}_{. Поэтому сила инерции}

_.

_{То есть её можно находить как сумму двух сил: нормальной силы инерции и касательной силы инерции.}

_{………………………………………………………………………………………………………………………………………………………………}

_{3 вопрос.}_{Меры инертности тел при вращательном и поступательном движении.}

_{Кинематика}_{рассматривает движение тел, не интересуясь причинами, обуславливающими это движение и его изменение.}

_{В основе}_{динамики, которая изучает причины изменения движения, лежат законы Ньютона}_{. Эти законы относятся к фундаментальным законам природы и доказать их справедливость или опровергнуть можно только опытом.}

_{Второй закон Ньютона}_{– основной закон динамики.}

_{Этот закон выполняется только в}_{инерциальных системах отсчета}_.

_{В динамике вводятся две новые физические величины – масса тела}_m_{и сила}_{, а также способы их измерения. Масса тела}_m_{является}_{количественной характеристикой}_{инертных свойств тела.}_{Она показывает, как тело реагирует на внешнее воздействие. Вторая – сила}_{является}_{количественной мерой действия одного тела на другое.}

_{Второй закон Ньютона – это фундаментальный закон природы; он является обобщением опытных фактов, которые можно разделить на две категории:}

_{1. Если на тела разной массы подействовать одинаковой силой, то ускорения, приобретаемые телами, оказываются обратно пропорциональны массам}

_{2. Если силами разной величины подействовать на одно то же тело, то ускорения тела оказываются прямо пропорциональными приложенным силам.}

_{Обобщая подобные наблюдения, Ньютон сформулировал основной закон динамики:}_{Сила, действующая на тело, равна произведению массы тела на сообщаемое этой силой ускорение:}

₍₁₎

_{Это и есть второй закон Ньютона. Он позволяет вычислить ускорение тела, если известна его масса}_m_{и действующая на тело сила}_:

₍₂₎

_{В международной системе единиц (СИ) за единицу силы принимается сила, которая сообщает телу массой 1 кг ускорение 1 м/с2. Эта единица называется}_{ньютоном (Н)}_.

_{Если на тело одновременно действуют несколько сил (например, и то под силой в формуле, выражающей второй закон Ньютона, нужно понимать}_{равнодействующую всех сил}_: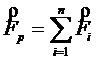

_{Если равнодействующая сила равна нулю, то тело будет оставаться в состоянии покоя или равномерного прямолинейного движения.}

_{Второй закон Ньютона также можно записать в виде:}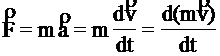

_(3).

_{Импульсом (количеством движения) называется векторная физическая величина, численно равная произведению массы тела на его скорость.}

_(4).

_{Основной единицей импульса тела в СИ является кг · м/с.}

_{Тогда второй закон Ньютона окончательно примет вид :}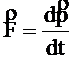

₍₅₎

_{Таким образом,}_{скорость изменения импульса тела равна действующей на него силе.}

_{Силы в природе.}

_{1) Сила всемирного тяготения. Сила тяжести. Вес тела.}

_{Закон всемирного тяготения}_{был сформулирован Ньютоном –}_{сила всемирного тяготения прямо пропорциональна произведению масс тел и обратно пропорциональна квадрату расстояния между центрами тел, т. е.}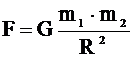

http://p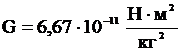andia.ru/text/78/157/images/image009_7.gif

₍₆₎

_где

_{- гравитационная постоянная,}_{численно равная силе взаимодействия двух тел единичной массы, находящихся на единичном расстоянии друг от друга.}

_{Сила всемирного тяготения является центральной силой, т. е. направленной вдоль прямой соединяющей центры тел.}

_{Под действием силы притяжения к Земле все тела падают с одинаковым ускорением, равным ускорению свободного падения}_{. Это означает, что на всякое тело массы m действует сила}_{, называемая}_{силой тяжести}_.

_{Когда тело покоится относительно Земли, сила тяжести уравновешивается}_{силой реакции опоры}_{(или подвеса), удерживающей тело от падения. По третьему закону Ньютона, тело будет действовать на опору (или подвес) с силой}_{, равной по величине}_{и противоположной ей по направлению, т. е.}_.

_{Сила, с которой тело действует на опору или подвес, вследствие притяжения к Земле, называется}_{весом тела.}

_{2) Силы трения.}

_{Силы трения появляются при перемещении двух соприкасающихся тел или частей тела относительно друг друга.}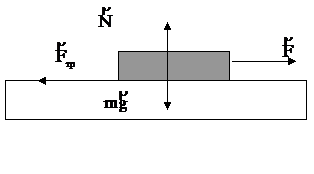

http://pandia.ru/text/78/157/images/image017_6.gif

_{Силы трения направлены по касательной к трущимся поверхностям, причем так, что они противодействуют относительному смещению этих поверхностей.}

_{В случае сухого трения, сила трения возникает не только при скольжении одной поверхности по другой, но также и при попытках вызвать такое смещение. В этом случае сила трения называется}_{силой трения покоя}_.

_{Опыт показывает, что максимальная сила трения покоя}_равна

₍₇₎

_{где N – сила нормального давления,}_{- безразмерный коэффициент, зависящий от рода соприкасающихся тел и чистоты обработки поверхности и называемый}_{коэффициентом трения.}

_{Следует иметь в виду, что, помимо сил трения, при движении в жидкости или газе возникают силы сопротивления среды, которые могут быть гораздо больше сил трения. Характерной особенностью этих сил является их зависимость от скорости движения тела и его формы.}

_2.

_{Если на вал с диском действуют две силы}_{, то простой опыт показывает, что равновесие имеет место только при условии, что}_{, т. е. когда}_{моменты сил}_{равны по величине и противоположны по направлению.}

_{Псевдовектор}

₍₈₎

_{называется}_{моментом силы}_{относительно точки О.}

_{Модуль вектора}_{определяется по формуле}

_{(9) ,}

_где

_{- плечо силы, т. е. кратчайшее расстояние от точки О до линии действия силы.}

_{Величину}

_{(10)называ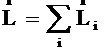ют}_{моментом импульса материальной точки относительно точки.}

_{Величину}

₍₁₁₎

_{называют}_{моментом импульса твердого тела относительно точки.}

_{Физическую величину}

₍₁₂₎

_{называют}_{моментом инерции материальной точки}_{относительно оси вращения, а величину}

₍₁₃₎

_{моментом инерции твердого тела.}

_{Любое твердое тело можно разбить на элементарные массы}

_{, расположенные на расстоянии}_{от оси вращения. Тогда момент инерции твердого тела может быть определен по формуле}

_{, где интегрирование должно быть распространено на весь объем тела.}

_{Момент инерции тела зависит от положения оси вращения. Для определения момента инерции тела относительно оси, не проходящей через центр масс, можно пользоваться}_{теоремой Гюйгенса – Штейнера}

_(14),

_где_{- момент инерции тела относительно оси, проходящей через центр масс,}_{- момент инерции относительно новой оси,}_{- расстояние между осями,}_{- масса тела.}

_{Момент инерции во вращательном движении играет ту же роль, что и масса в поступательном движении, т. е. является мерой инертности тела во вращательном движении.}

_{Второй закон Ньютона для вращающегося тела можно записать в виде:}

_(15).

_{Так как}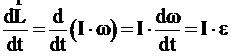

_{, то можно найти и другую форму записи данного закона:}

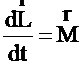http://pandia.ru/text/78/157/images/image042_1.gif

_(16).

_{Это выражение получило название}_{основного уравнения динамики вращательного движения.}

_{…………………………………………………………………………………………………………………………..}

_{4 вопрос .}_{Дифференциальные уравнения движении материальной точки}

_{Пусть на материальную точку действуют одновременно несколько сил, среди которых есть как постоянные, так переменные силы.}

_{Запишем второй закон динамики в виде}

_,

_{В проекциях на оси декартовых координат}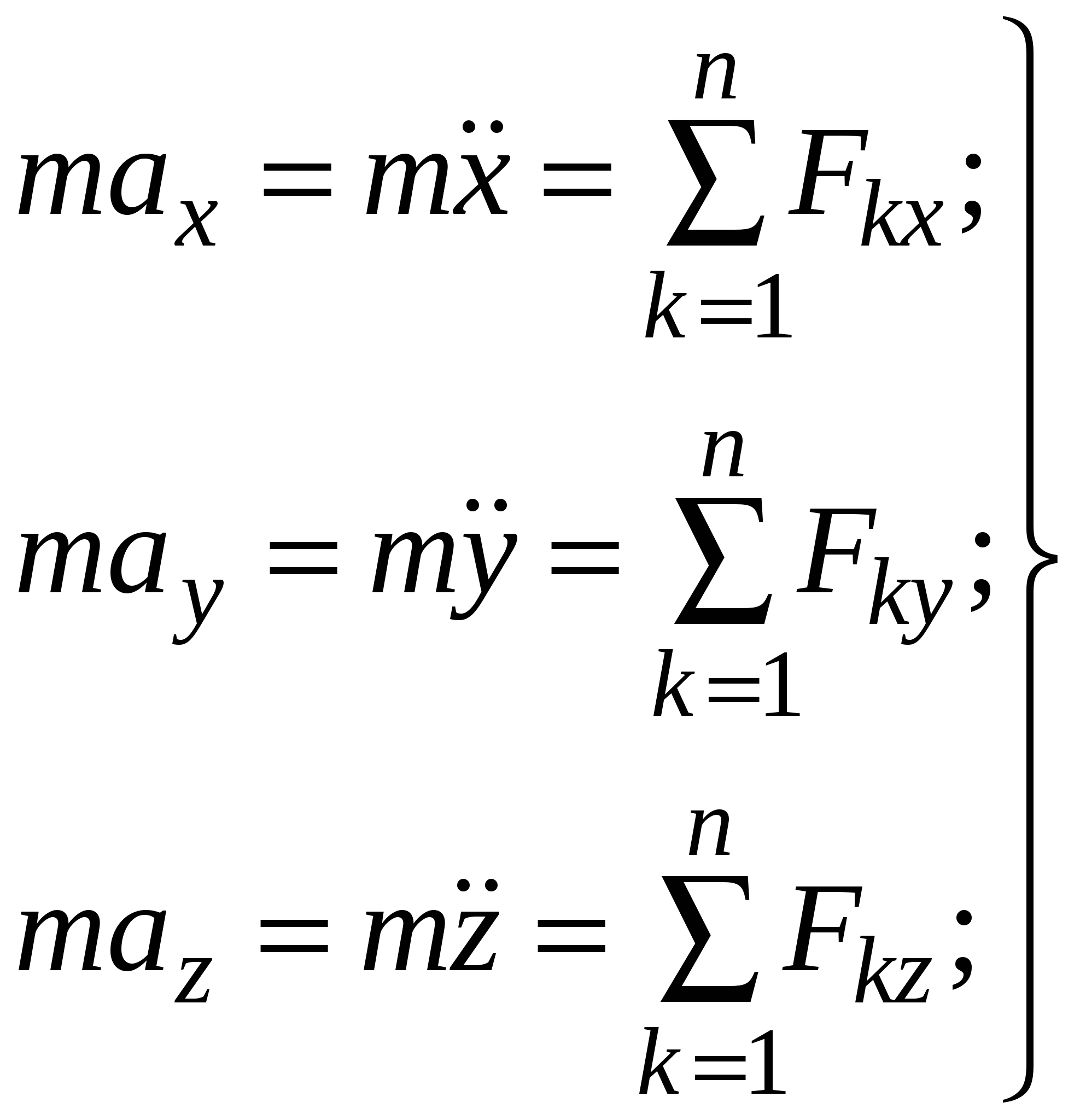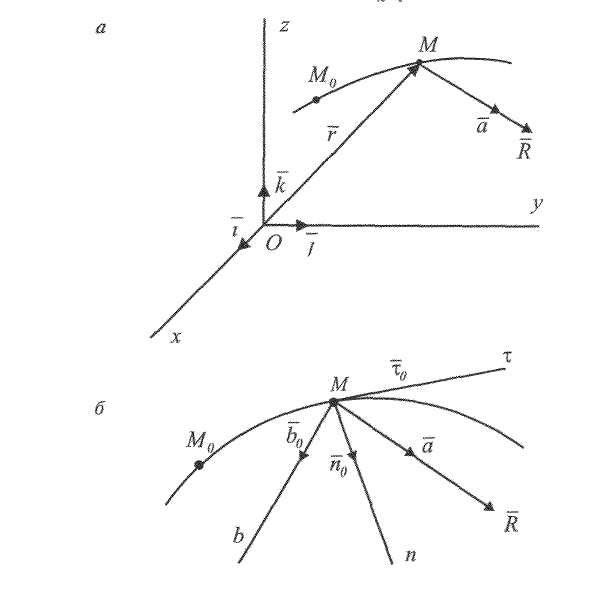

http://www.studfiles.ru/html/2706/252/html_wswaqwgjuj.rjk0/htmlconvd-dbkzcl_html_m2409c8c8.gif

http://www.studfiles.ru/html/2706/252/html_wswaqwgjuj.rjk0/htmlconvd-dbkzcl_html_m7c7ae7b3.jpg

_{В проекциях на естественные оси}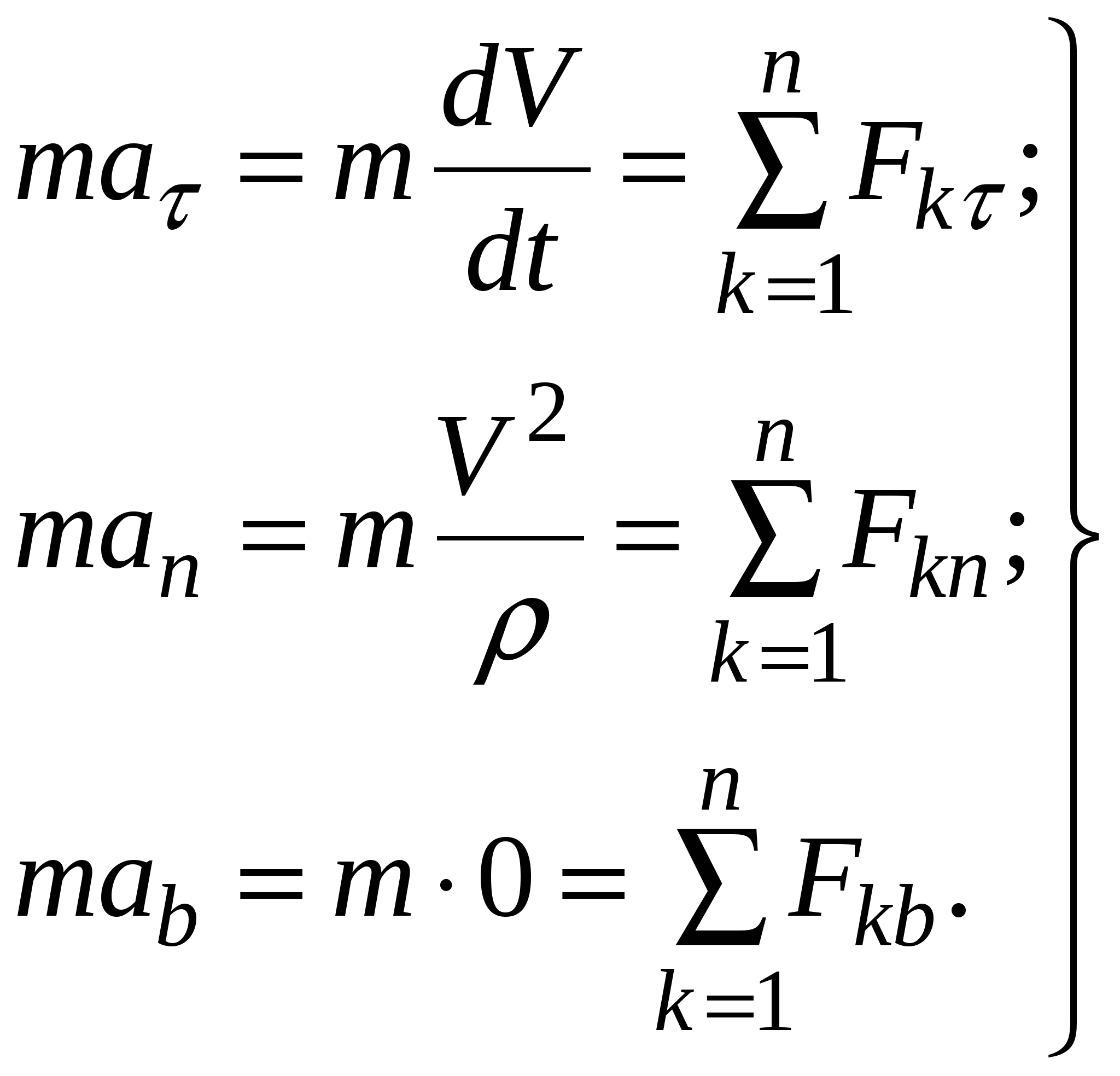

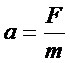http://www.studfiles.ru/html/2706/252/html_wswaqwgjuj.rjk0/htmlconvd-dbkzcl_html_69ae3572.gif

1 2 3 4 5 6 7 8 9 10 11