1 вопрос. Динамика точки. Основные понятия и определения
 Скачать 1.54 Mb. Скачать 1.54 Mb.
|
23 вопрос. Теорема об изменении кинетического моментаКинетический момент механической системы относительно неподвижного центра O является мерой движения системы вокруг этого центра. При решении задач обычно применятся не сам вектор , а его проекции на оси неподвижной системы координат, которые называются кинетическими моментами относительно оси. Например, - кинетический момент системы относительно неподвижной оси Oz . Кинетический момент механической системы складывается из кинетических моментов точек и тел, входящих в эту систему. Рассмотрим способы определения кинетического момента материальной точки и твердого тела при различных случаях их движения. Для материальной точки с массой , имеющей скорость , кинетический момент относительно некоторой оси Oz определяется как момент вектора количества движения этой точки относительно выбранной оси: Кинетический момент точки считается положительным, если со стороны положительного направления оси движение точки происходит против часовой стрелки. Если точка совершает сложное движение, для определения ее кинетического момента следует вектор количества движения рассматривать как сумму количеств относительного и переносного движений (рис.41) Тогда Но , где - расстояние от точки до оси вращения, и 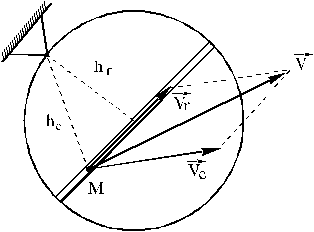 Рис. 41 Вторую составляющую вектора кинетического момента можно определить так же, как и момент силы относительно оси. Как и для момента силы, величина равна нулю, если вектор относительной скорости лежит в одной плоскости с осью переносного вращения. Кинетический момент твердого тела относительно неподвижного центра можно определить как сумму двух составляющих: первая из них характеризует поступательную часть движения тела вместе с его центром масс, вторая - движение системы вокруг центра масс: Если тело совершает поступательное движение, то вторая составляющая равна нулю . Наиболее просто вычисляется кинетической момент твердого тела при его вращении вокруг неподвижной оси , где - момент инерции тела относительно оси вращения. Теорема об изменении кинетического момента механической системы при ее движении вокруг неподвижного центра формулируется следующим образом: полная производная по времени от вектора кинетического момента механической системы относительно некоторого неподвижного центра O по величине и направлению равна главному моменту внешних сил, приложенных к механической системе, определенному относительно того же центра где При решении задач, в которых рассматриваются тела, вращающиеся вокруг неподвижной оси, используют теорему об изменении кинетического момента относительно неподвижной оси Как и для теоремы о движении центра масс, теорема об изменении кинетического момента имеет следствия. Следствие 1. Если главный момент всех внешних сил относительно некоторого неподвижного центра равен нулю, то кинетический момент механической системы относительно этого центра остается неизменным. Следствие 2. Если главный момент всех внешних сил относительно некоторой неподвижной оси равен нулю, то кинетический момент механической системы относительно этой оси остается неизменным. Теорема об изменении кинетического момента применяется для решения задач, в которых рассматривается движение механической системы, состоящей из центрального тела, вращающегося вокруг неподвижной оси, и одного или нескольких тел, движение которых связано с центральным.. Связь может осуществляться при помощи нитей, тела могут перемещаться по поверхности центрального тела или в его каналах за счет внутренних сил. С помощью данной теоремы можно определить зависимость закона вращения центрального тела от положения или движения остальных тел………………………………………………………………………………………………………………………….. |
