1 вопрос. Динамика точки. Основные понятия и определения
 Скачать 1.54 Mb. Скачать 1.54 Mb.
|
|
Пример 4.2 Момент инерции тонкого стержня. Длина стержня l, масса m. Найти момент инерции относительно оси, проходящей перпендикулярно стержню через его центр (рис. 4.7) и через один из его концов. Сначала найдем момент инерции относительно оси, проходящей через центр стержня. Выделим элемент длины стержня длиной dx на расстоянии x оси вращения. Тогда масса этого элемента равна 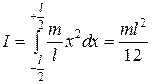 . . Рис. 4.7 Момент инерции относительно оси, проходящей через один из его концов, найдем с помощью теоремы Штейнера (4.16): 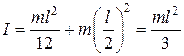 . .В таблице 1 приведены формулы для вычисления моментов инерции однородных тел простейшей формы. Таблица 1
………………………………………………………………………………………………………………………………… 33 вопрос. Принцип Д’Аламбера. Все методы решения задач динамики, которые мы до сих пор рассматривали, основываются на уравнениях, вытекающих или непосредственно из законов Ньютона, или же из общих теорем, являющихся следствиями этих законов. Однако, этот путь не является единственным. Оказывается, что уравнения движения или условия равновесия механической системы можно получить, положив в основу вместо законов Ньютона другие общие положения, называемые принципами механики. В ряде случаев применение этих принципов позволяет, как мы увидим, найти более эффективные методы решения соответствующих задач. В этой главе будет рассмотрен один из общих принципов механики, называемый принципом Даламбера. Пусть мы имеем систему, состоящих из nматериальных точек. Выделим какую-нибудь из точек системы с массой . Под действием приложенных к ней внешних и внутренних сил и (в которые входят и активные силы, и реакции связи) точка получает по отношению к инерционной системе отсчета некоторое ускорение . Введем в рассмотрение величину , имеющую размерность силы. Векторную величину, равную по модулю произведению массы точки на ее ускорение и направленную противоположно этому ускорению, называют силой инерции точки(иногда даламберовой силой инерции). Тогда оказывается, что движение точки обладает следующим общим свойством: если в каждый момент времени к фактически действующим на точку силам и прибавить силу инерции , то полученная система сил будет уравновешенной, т.е. будет . Это выражение выражает принцип Даламбера для одной материальной точки. Нетрудно убедиться, что оно эквивалентно второму закону Ньютона и наоборот. В самом деле, второй закон Ньютона для рассматриваемой точки дает . Перенося здесь член в правую часть равенства и придем к последнему соотношению. Повторяя проделанные высшее рассуждения по отношению к каждой из точек системы, придем к следующему результату, выражающему принцип Даламбера для системы:если в любой момент времени к каждой из точек системы, кроме фактически действующих на ней внешних и внутренних сил, приложить соответствующие силы инерции, то полученная система сил будет находиться в равновесии и к ней можно будет применять все уравнения статики. Значение принципа Даламбера состоит в том, что при непосредственном его применении к задачам динамики уравнения движения системы составляются в форме хорошо известных уравнений равновесия; что делает единообразный подход к решению задач и обычно намного упрощает соответствующие расчёты. Кроме того, в соединении с принципом возможных перемещений, который будет рассмотрен в следующей главе, принцип Даламбера позволяет получить новый общий метод решения задач динамики. Применяя принцип Даламбера, следует иметь в виду, что на точку механической системы, движение которой изучается, действуют только внешние и внутренние силы и , возникающие в результате взаимодействия точек системы друг с другом и с телами, не входящими в систему; под действием этих сил точки системы и движутся с соответствующими ускорениями . Силы же инерции, о которых говорится в принципе Даламбера, на движущиеся точки не действуют (иначе, эти точки находились бы в покое или двигались без ускорений и тогда не было бы и самих сил инерции). Введение сил инерции - это лишь приём, позволяющий составлять уравнения динамики с помощью более простых методов статики. Из статики известно, что геометрическая сумма сил, находящихся в равновесии, и сумма их моментов относительно любого центра Оравны нулю, причём по принципу отвердевания это справедливо для сил, действующих не только на твёрдое тело, но и на любую изменяемую систе6му. Тогда на основании принципа Даламбера должно быть: 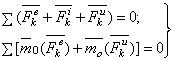 Введём обозначения: Величины и представляют собой главный вектор и главный момент относительно центра Осистемы сил инерции. В результате, учитывая, что геометрическая сумма внутренних сил и сумма их моментов равны нулю, получим из равенств: , (1) Применение уравнений (1), вытекающих из принципа Даламбера, упрощает процесс решения задач, т.к. эти уравнения не содержат внутренних сил. В проекциях на оси координат эти равенства дают уравнения, аналогичные соответствующим уравнениям статики. Чтобы пользоваться этими уравнениями при решении задач, надо знать выражение главного вектора и главного момента сил инерций. ……………………………………………………………………………………………………………………………… 34 вопрос. Предмет и основные понятия аналитической механики СВЯЗИ И ИХ КЛАССИФИКАЦИЯ Система материальных точек называется свободной,если положение отдельных её точек и их скорости могут принимать произвольное значение. Несвободной - если на положение и скорости точек системы наложены ограничения геометрического или кинематического характера, называемыми связями. Связями называют любого вида ограничения, налагаемые на положения (координаты) и скорости точек механической системы. Конструктивно связи осуществляются в виде нитей, стержней, шарниров, опор, поверхностей и т.д. Аналитически связи выражаются уравнениями или неравенствами, т.е. соотношениями между радиус - векторами точек системы, их скорости и времени. Связи можно разделить на два типа: удерживающие (двухсторонние)и неудерживающие (односторонние). Удерживающимисвязями называются связи, которые сохраняют свое действие во все время движения точек системы. Аналитически эти связи выражаются уравнениями, связывающие координаты точек, их скорости и время 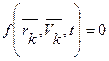 , ,здесь -радиус вектор, определяющий положение k-той точки системы, -ее скорость, t -время. Примером удерживающей связи может служить система из двух материальных точек т1и т2,которые соединены стержнем постоянной длины L. Вэтом случае уравнение связи имеет вид 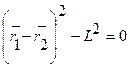 . .Неудерживающимисвязями называются связи, которые могут в некоторые промежутки времени меняться. Аналитически они выражаются неравенством, связывающим координаты точек системы, их скорости и время 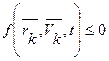 . .Примером неудерживающей связи может служить система из двух материальных точек, которые соединены гибкой нитью длинной L.В этом случае уравнение связи имеет вид 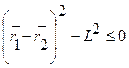 / /В дальнейшем будем рассматривать только удерживающие связи. 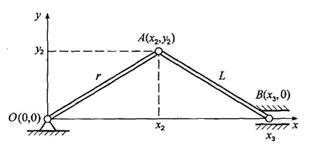 Связь называется стационарной,если она не меняется с течением времени. В уравнение стационарной связи не входит время tв явном виде. Связь называется стационарной,если она не меняется с течением времени. В уравнение стационарной связи не входит время tв явном виде.Примером механизма, имеющего стационарные связи, может служить кривошипно-шатунный механизм. Механизм состоит из кривошипа ОАдлинной r,шатуна АВдлинной Lи ползуна В. Уравнения связи данного механизма запишутся: Первое уравнение определяет постоянную длину кривошипа, второе - постоянную длину шатуна. Связь называется нестационарной,если она меняется с течением времени. Уравнение такой связи содержит время tявно. Например, материальная точка может двигаться только по поверхности. Пусть уравнение поверхности задано в виде функции f(х,у,z) = 0. Это стационарная связь. Если поверхность подвижная или деформирующаяся, то в уравнение поверхности время гвойдет явно: f(х,у,z,t) = 0. В этом случае связь нестационарная. Примером нестационарной связи является, также деформируемое твердое тело. Связь называется конечнойили геометрической,если она накладывает ограничения только на координаты точек системы. Уравнение конечной (геометрической) связи имеет вид 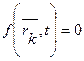 . .Эта связь не налагает ограничение на скорости точек системы. В общем случае удерживающая связь называется кинематическойили дифференциальной.Эта связь налагает ограничения на положение координат точек системы и на скорости этих точек. Если кинематическая (дифференциальная) связь интегрируется, то после интегрирования связь перестает быть таковой и становиться конечной (геометрической) связью. Следовательно, связь будет кинематической (дифференциальной) только в том случае, если она неинтегрируемая. Система называется склерономной,если на нее наложены только стационарные связи. В противном случае система называется реономной. Голономной называется всякая свободная система материальных точек, а также несвободная система с конечными или дифференциальными, но интегрируемыми связями. При наличии дифференциальных неинтегрируемых связей, система называется неголономной. 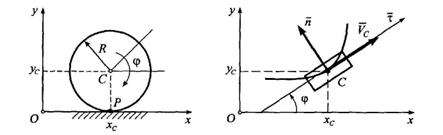 Рассмотрим пример голономной связи. Колесо радиуса Rкатиться без скольжения по прямолинейному рельсу. Рассмотрим пример голономной связи. Колесо радиуса Rкатиться без скольжения по прямолинейному рельсу.Положение колеса в плоскости движения хОуопределяется координатами центра колеса (полюса) хс, уси углом поворота φ. Если ось Охнаправить вдоль рельса, то ус= R,следовательно, наложено ограничение на координату у,связь - конечная (геометрическая). Кроме того, должна быть равна нулю скорость точки Р,точки касания колеса с рельсом. Это условие запишется в виде уравнения .. Последнее уравнение накладывает ограничения на скорости, поэтому связь будет дифференциальной (кинематической). Но это уравнение сразу интегрируется и приводит к соотношению между координатами хси φ, имеющему вид хс=Rφ.Таким образом, рассмотренная система является голономной. В качестве примера неголономной связи рассмотрим движение конька по поверхности льда. При отсутствии скольжения вектор скорости центра тяжести конька С должен быть направлен по касательной к траектории движения - по оси т Имеем: ,где φ - угол, образованный осью хи касательной к траектории движения в точке С -осью . Разделив второе соотношение на первое, получим , откуда .Таким образом получено уравнение, накладывающее ограничения на скорость. Это уравнение не может быть проинтегрировано, поскольку угол φ - переменный (угол φ=φ(t) определяет направление оси , поэтому это уравнение является уравнением неголономной связи. Силы, приложенные к точкам системы, обычно классифицируют двумя способами. По первому способу, совокупность всех сил, приложенных к точкам материальной системы, разделяют на внутренние и внешние силы. Внутренними силами()называют силы взаимодействия между точками, образующими материальную систему. Внешними силами()называют силы, возникающие благодаря воздействию на точки системы других материальных точек, не входящих в эту систему. В соответствии со вторым способом классификации, совокупность всех сил, приложенных к точкам материальной системы, разделяют на активныеипассивные силы.Силы, которые создают или способны создавать движение твердого тела, называются активными силами. Силы, не создающие движение, но ограничивающие перемещения твердого тела (например, реакции опор) относятся к пассивным силам. Отметим, что деление системы сил на внутренние и внешние силы и на активные и пассивные силы не взаимосвязаны. Для задач, связанных с механикой деформируемого твердого тела используют первую классификацию: делят совокупность приложенных к точкам материальной системы сил на внутренние и внешние. В аналитической механике эффект действия силы на тело определяется бесконечно малыми перемещениями тела, допускаемые наложенными связями. 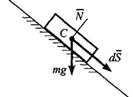 Так, для груза, расположенного на наклонной плоскости, таким перемещением (допускаемым связью) будет перемещение -движение груза вдоль наклонной плоскости. Так, для груза, расположенного на наклонной плоскости, таким перемещением (допускаемым связью) будет перемещение -движение груза вдоль наклонной плоскости.В классической механике Ньютона применялась аксиома связей, в соответствии с которой эффект влияния связи учитывался мысленным освобождением тела от наклонной поверхности, а ее действие на тело заменялась силой N - реакцией связи. В аналитической механике эффект действия связи определяется возможными перемещениями точек. |
