1 вопрос. Динамика точки. Основные понятия и определения
 Скачать 1.54 Mb. Скачать 1.54 Mb.
|
|
асимптотически устойчивым. Достаточное условие устойчивости положения равновесия консервативной системы определяется теоремой Лагранжа: достаточным условием устойчивости положения равновесия консервативной системы является наличие в нем локального (изолированного) минимума потенциальной энергии. Однако в реальной механической системе всегда существуют силы сопротивления движению, возникающие благодаря трению или вязкости среды. Такие силы Кельвином названыдиссипативными. При наличии в системе диссипативных сил для оценки устойчивости положения равновесия можно дополнительно воспользоваться тремя теоремами Кельвина. 1. Если положение равновесия консервативной системы устойчиво при одних только потенциальных силах, то оно будет оставаться устойчивым и при добавлении диссипативных сил. 2. Устойчивое положение равновесия становится асимптотически устойчивым при добавлении диссипативных сил с полной диссипацией. 3. Изолированное и неустойчивое при одних потенциальных силах положение равновесия не может быть стабилизировано диссипативными силами. Доказательства этих теорем могут быть получены как следствие теоремы Ляпунова об устойчивости движения, выходящей за рамки данного курса. Первые две теоремы Кельвина указывают на то, что диссипативные силы не могут нарушить устойчивость положения равновесия, а третья — что диссипативные силы не в состоянии трансформировать неустойчивое положение равновесия консервативной системы в устойчивое. Следовательно, для оценки устойчивости положения равновесия реальную колебательную систему с диссипативными силами можно заменить ее консервативной моделью. Теорема Лагранжа-Дирихле (критерий устойчивости поожения равновесия механической системы): Для устойчивости положения равновесия механической системы подчиненной галономным, стационарным, идеальным или неосвобождающим связям и находящихся в стационарном силовом поле, достаточно, чтобы потенциальная энергия в положении равновесия имела изолированный относительный минимум. ………………………………………………………………………………………… 47вопрос Колебания. Форма колебаний. Виды колебаний. Классификация. Характеристики колебательного процесса. Условия возникновения механических колебаний. Гармонические колебания. Колеба́ния — повторяющийся в той или иной степени во времени процесс изменения состояний системы около точки равновесия. Колебательные процессы широко распространены в природе и технике, например качание маятника часов, переменный электрический ток и т. д. Физическая природа колебаний может быть разной, поэтому различают колебания механические, электро магнитные и др. Однако различные колебательные процессы описываются одинаковы ми характеристиками и одинаковыми уравнениями. Отсюда следует целесообразность единого подхода к изучению колебаний различной физической природы. Форма колебаний может быть разной. Колебания называются периодическими, если значения физических величин, изменяющихся в процессе колебаний, повторяются через равные промежутки времени рис.1. (В противном случае колебания называются апериодическими). Выделяют важный частный случай гармонических колебаний (рис.1). Колебания, приближающиеся к гармоническим называются квазигармоническими. 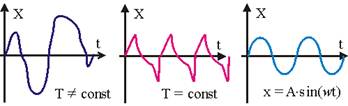 Рис.1. Виды колебаний Колебания различной физической природы имеют много общих закономерностей и тесно взаимосвязаны c волнами. Исследованиями этих закономерностей занимается обобщённая теория колебаний и волн. Принципиальное отличие от волн: при колебаниях не происходит переноса энергии, это, локальные, «местные» преобразования энергии. Виды колебаний. Колебания различаются по природе: механические (движение, звук, вибрация), электромагнитные (например, колебания в колебательном контуре, объёмном резонаторе, колебания напряжённостей электрического и магнитного полей в радиоволнах, волнах видимого света и любых др. электромагнитных волнах), электромеханические (колебания мембраны телефона, пьезокварцевого или магнитострикционного излучателя ультразвука); химические (колебания концентрации реагирующих веществ, при так называемых периодических химических реакциях); термодинамические (например, так называемое поющее пламя и др. тепловые автоколебания, встречающиеся в акустике, а также в некоторых типах реактивных двигателей); колебательные процессы в космосе (большой интерес в астрофизике представляют колебания яркости звезд цефеид (пульсирующие переменные звезды сверхгиганты, изменяющие блеск с амплитудой от 0,5 до 2 звезной величины и периодом от 1 до 50 суток); Таким образом, колебания охватывают огромную область физических явлений и технических процессов. Классификация колебаний по характеру взаимодействия с окружающей средой : свободные (или собственные) — это колебания в системе под действием внутренних сил, после того как система выведена из состояния равновесия (в реальных условиях свободные колебания почти всегда затухающие). Например, колебания груза на пружине, маятника, моста, корабля на волне, струны; колебания плазмы, плотности и давления воздуха при распространении в нём упругих (акустических) волн. Чтобы свободные колебания были гармоническими, необходимо, чтобы колебательная система была линейной (описывалась линейными уравнениями движения), и в ней отсутствовала диссипация энергии (последняя вызвает затухание). вынужденные — колебания, протекающие в системе под влиянием внешнего периодического воздействия. При вынужденных колебаниях может возникнуть явление резонанса: резкое возрастание амплитуды колебаний при совпадении собственной частоты осциллятора и частоты внешнего воздействия. автоколебания — колебания, при которых система имеет запас потенциальной энергии, расходующейся на совершение колебаний (пример такой системы — механические часы). Характерным отличием автоколебаний от свободных колебаний является, то, что их амплитуда определяется свойствами самой системы, а не начальными условиями. параметрические — колебания, возникающие при изменении какого-либо параметра колебательной системы в результате внешнего воздействия, случайные — колебания, при которых внешняя или параметрическая нагрузка является случайным процессом, связанные колебания - свободные колебания взаимно связанных систем, состоящих из взаимодействующих одиночных колебательных систем. Связанные колебания имеют сложный вид вследствие того, что колебания в одной системе влияют через связь (в общем случае диссипативную и нелинейную) на колебания в другой колебания в структурах с распределенными параметрами (длинные линии, резонаторы), флуктуационные, происходящие в результате теплового движения вещества. . Условия возникновения колебаний. 1. Для возникновения колебания в системе необходимо вывести её из положения равновесия. Например, для маятника сообщив ему кинетическую (удар, толчок), либо – потенциальную (отклонение тела) энергию. 2. При выведении тела из положения устойчивого равновесия возникает равнодействующая сила, направленная к положению равновесия. С энергетической точки зрения это значит, что возникают условия для постоянного перехода (кинетической энергии в потенциальную, энергии электрического поля в энергию магнитного поля и обратно. 3. Потери энергии системы за счет перехода в другие виды энергии (часто в тепловую энергию) малы. Характеристики колебательного процесса. На рис.1 представлен график периодического изменения функции F(x), которое характеризуется параметрами: Амплитуда — максимальное отклонение колеблющейся величины от некоторого усреднённого её значения для системы. Период — наименьший промежуток времени, через который повторяются какие-либо показатели состояния системы (система совершает одно полное колебание), T(c). 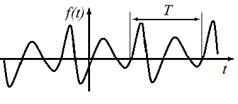 ………………………………………………………………………………………………………………………………. 48 вопрос. Свободные колебания в среде без сопротивления. Пусть точка массы движется вдоль горизонтальной прямой под действием восстанавливающей силы (рис.6). Прямолинейное движение материальной точки под действием только восстанавливающей силы называется свободным колебанием точки. Для изучения свободного колебания составим дифференциальное уравнение движения точки, которое в данном случае имеет вид: Разделив на массу точки , и обозначив , запишем окончательно Полученное уравнение называется дифференциальным уравнением свободных колебаний материальной точки. Для интегрирования этого однородного линейного дифференциального уравнения второго порядка с постоянными коэффициентами составим характеристическое уравнение . Его корни—числа мнимые и , следовательно, общее решение дифференциального уравнения (2.2) имеет вид где и —постоянные интегрирования, определяемые начальными условиями. В качестве начальных условий зададим начальное положение точки и начальную скорость, т. е. при , , . Чтобы определить значения постоянных интегрирования и найдем уравнение, определяющее скорость точки, продифференцировав уравнение (2.3): Подставив начальные условия в уравнения (2.3) и (2.4), найдем , , откуда . После подстановки найденных значений и в (2.3) получаем уравнение движения рассматриваемой точки: 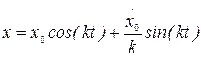 . .Уравнению (2.5) можно придать другой вид, введя вместо постоянных и две другие постоянные и , положив ; . Выражение (2.3) примет следующий вид: Произвольные постоянные и , как и и находятся по начальным условиям. Для их определения выразим и через и : Откуда 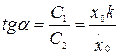 , , Значение амплитуды считаем положительным, угол изменяется в пределах от до . Поэтому для его определения надо кроме величины тангенса знать еще знак синуса этого угла. Окончательно, уравнение движения точки определяется следующим уравнением 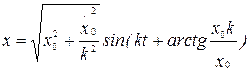 . .Уравнение —уравнение гармонических колебаний точки. Таким образом, установлено, что свободные колебания материальной точки под действием линейной восстанавливающей силы являются гармоническими колебаниями. Так как , то частота и период свободных колебаний определяются по формулам: 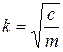 , ,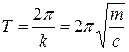 . .Как видно, частота и период свободных колебаний точки зависят только от массы этой точкии от коэффициента, характеризующего восстанавливающую силу, и не зависят от начальных условий движения. Период свободных колебаний увеличивается при увеличении массы точки и уменьшается при увеличении коэффициента . Независимость периода колебаний от начальных условий называется изохронностью,а движение с таким периодом—изохронным. ………………………………………………………………………………………………………………………… 49 вопрос. Вынужденные колебания при отсутствии сопротивления. Рассмотрим колебания материальной точки, на которую кроме восстанавливающей силы действует еще , проекция которой на ось , направленную по траектории точки, изменяется по гармоническому закону Эта сила называется возмущающей силой, а колебания, происходящие при действии такой силы, называются вынужденными. —амплитуда возмущающей силы; —частота возмущающей силы; —фаза изменения возмущающей силы; —начальная фаза изменения возмущающей силы. Пусть на прямолинейно движущуюся точку массы кроме восстанавливающей силы , пропорциональной отклонению точки от положения равновесия, действует только возмущающая сила .Точка с приложенными к ней силами и оси координат изображены на рис.11. Основное уравнение динамики точки имеет вид: |
