1 вопрос. Динамика точки. Основные понятия и определения

• Название: 1 вопрос. Динамика точки. Основные понятия и определения
• Дата: 19.06.2018
• Размер: 1.54 Mb.
• Имя файла: teor_mekh_ekz.docx
• Тип: Документы; #47316
• страница: 7 из 11

Кинетическая энергия материальной точки и системы. Теорема Кенига

<sub>Кинетическую энергию материальной точки массой m, движущейся с абсолютной скоростью , определяют по формуле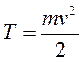



где 

Кинетическая энергия механической системы равна сумме кинетических энергий всех точек этой системы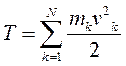



Теорема Кенига.

Кинетическая энергия механической системы в её абсолютном движении равна сумме кинетической энергии центра масс, в предположении, что в нём сосредоточена масса всей системы, и кинетической энергии движения системы относительно центра масс.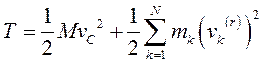



Рассмотрим движение механической системы в неподвижной системе отсчета Oxyz. В качестве подвижной выберем систему CXYZ с началом в центре масс, движущуюся поступательно вместе с центром масс. Абсолютное движение механической системы при этом можно рассматривать как совокупность переносного (вместе с ЦМ) и относительного (по отношению к ЦМ) движений системы.

Для любого момента времени положение произвольной точки по отношению к неподвижному центру О



где - радиус-вектор точки по отношению к ЦМ. Продифференцируем и найдем абсолютную скорость:



Учитывая, что квадрат вектора равен квадрату его модуля,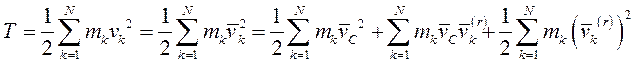



Здесь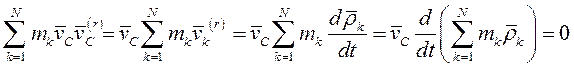



поскольку сумма статических моментов масс точек относительно центра масс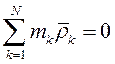 

Таким образом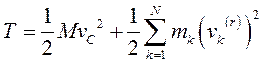



где 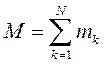- масса механической системы.

………………………………………………………………………………………………………………………………

30 вопрос .Кинетическая энергия твёрдого тела в различных случаях его движения.

При поступательном движении твёрдого тела скорости всех его точек одинаковы и равны скорости центра масс, поэтому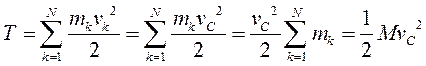



При вращении твёрдого тела вокруг неподвижной оси скорость его произвольной точки



- кратчайшее расскояние от точки 

Тогда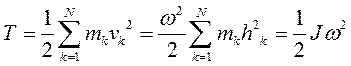



При плоском движении твёрдого тела относительная скорость произвольной точки 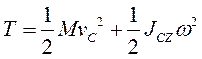и, следовательно, согласно формуле Кенига



При сферическом движении твёрдого тела скорость произвольной точки определяется формулой Эйлера



преобразуем формулу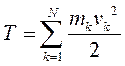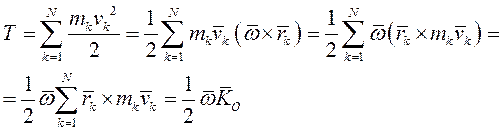 



С учетом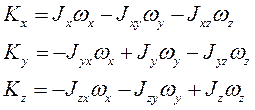



кинетическую энергию твёрдого тела при сферическом движении можно записать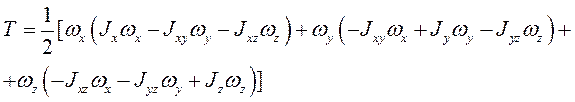



Если оси Oxyz направить по главным осям инерции тела для точки О, то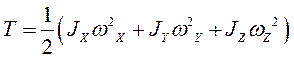



В общем случае движения свободного твёрдого тела в пространстве, которое можно рассматривать как совокупность поступательного переносного движения вместе с центром масс и сф. движения по отношению к этому центру, относительная скорость произвольной точки тела и, следовательно, кинетическая энергия тела</sub>

…………………………………………………………………………………………………………………………………….

<sub>31 вопрос. Момент инерции твердого тела

Момент инерции – это величина, зависящая от распределения масс в теле и являющаяся, наряду с массой, мерой инертности тела при непоступательном движении. При вращении твердого тела вокруг неподвижной оси момент инерции тела относительно этой оси определяется выражением

,

где- элементарные массы тела;- их расстояния от оси вращения.

Момент инерции тела относительно какой-либо оси можно найти вычислением. Если вещество в теле распределено непрерывно, то вычисление момента инерции сводится к вычислению интеграла

, (1)

где – масса элемента тела, находящегося на расстоянииот интересующей нас оси. Интегрирование должно производиться по всему объему тела.

Аналитическое вычисление таких интегралов возможно только в простейших случаях тел правильной геометрической формы.

Если известен момент инерции тела относительно какой-либо оси, можно найти момент инерции относительно любой другой оси, параллельной данной. Используя теорему Штейнера, согласно которой момент инерции тела относительно произвольной оси равен сумме момента инерции тела относительно оси, проходящей через центр масс телаи параллельной данной оси, и произведения массы телат на квадрат расстояния между осями :

(2)

Вычисление момента инерции тела относительно оси часто можно упростить, вычислив предварительномомент инерции относительно точки. Сам по себе момент инерции тела относительно точки не играет никакой роли в динамике. Он является чисто вспомогательным понятием, служащим для упрощения вычислений.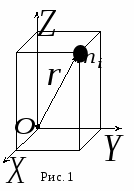

Рассмотрим некоторую точку твердого тела массой и с координатами относительно прямоугольной системы координат (рис. 1). Квадраты расстояний ее до координатных осейравны соответственноа моменты инерции относительно тех же осей

(3)

Сложив эти равенства и просуммировав по всему объему тела

(4)

получим

(5)

где – момент инерции телаотносительно точки.

Из этого выражения можно получить связь между моментами инерции плоского тела, относительно осей . Пусть масса плоского тела сосредоточена в плоскости т.е. координата любой точки такого тел равна нулю, тогда из

уравнений (3) и (4) следует, что



или

(6)

………………………………………………………………………………………………………………………………….

32 вопрос. Вычисление моментов инерции.

Уравнение (5.12) называют основным уравнением динамики вращения. Из него следует, что угловое ускорение e твердого тела, вращающегося вокруг неподвижной оси, прямо пропорционально результирующему моменту относительно этой оси всех внешних сил, действующих на тело, и обратно пропорционально моменту инерции тела относительно той же оси.

Таким образом, момент инерции тела является мерой его инертности при вращательном движении вокруг неподвижной оси: при одном и том же значении момента сил Mzтело с большим моментом инерции приобретает меньшее угловое ускорение ε.

Для определения момента инерции твердого тела относительно оси его разбивают на элементарные массы и сумму в выражении (4.11) заменяют интегралом:

, (5.14)

где ρ – плотность тела. Интегрирование выполняется по всему объему тела.

При вычислении осевого момента инерции твердого тела используются следующие его основные свойства.

1. Аддитивность. Момент инерции тела равен алгебраической сумме моментов инерции отдельных его частей.

2. Теорема Штейнера. Эта теорема применяется для расчета моментов инерции тел, если ось вращения не проходит через центр инерции тела (его центр масс): момент инерции I тела относительно произвольной оси равен сумме момента инерции тела относительно оси, проходящей через центр массы С данного тела и параллельной заданной оси, и произведения массы m тела на квадрат расстояния между этими осями (рис. 5.4)

I = IC + md2. (5.15)



Рис.5.4</sub>