1 вопрос. Динамика точки. Основные понятия и определения
 Скачать 1.54 Mb. Скачать 1.54 Mb.
|
25 вопрос. Дифференциальное уравнение вращательного движения твердого тела вокруг неподвижной осиДля изучения вращательного движения твердого тела вокруг неподвижной оси воспользуемся теоремой об изменении момента количества движения (кинетического момента) механической системы относительно оси (3.10): dKz/dt = Mze. (3.11) Пусть на твердое тело, имеющее неподвижную ось вращения z (рисунок 3.4), действует система заданных внешних активных сил (F1, F2, F3,...,Fn ), определяющих угловую скорость ω и угловое ускорение ε этого тела в его вращательном движении вокруг оси z. Одновременно на это же тело действуют силы реакции RA подпятника и RB радиального подшипника. Определяем правую часть уравнения (3.11): Mze=∑Mz(Fje)+Mz(RA)+ Mz(RB). Поскольку Mz(RA)= Mz(RB)= 0, то Mвращ = Mze=∑Mz(Fje). Найдем момент количества движения (кинетический момент) Kz вращающегося твердого тела. Для этого выделим точку Mj тела на расстоянии rj от оси вращения и имеющую скорость Vj = ω⋅rj. Очевидно, что Kzj= mj ⋅Vj ⋅rj= mj ⋅ω ⋅rj2. Тогда момент количества движения (кинетический момент) всего вращающегося тела будет: Kz = ∑Kzj = ∑mj ⋅ω ⋅rj2, где ∑mj ⋅rj2 = Jz. Следовательно, окончательно будем иметь Kz = Jz⋅ω. (3.12) Подставляя в уравнение (3.11) выражение (3.12), получаем Jz ⋅dω/dt = Mвращ, или Jz ⋅d2φ/dt2 = Mвращ. (3.13) Уравнение (3.13) представляет собой дифференциальное уравнение вращательного движения твердого тела вокруг неподвижной оси. Поскольку dω/dt = ε, имеем ε=Mвращ/Jz. (3.14) Полученное выражение (3.14) показывает, что осевой момент инерции Jz тела следует рассматривать как меру инертности твердого тела при его вращательном движении вокруг неподвижной оси. ……………………………………………………………………………………………………………………………………. 26 вопрос .Элементарная работа и ее аналитическое выражение Элементарная работа dA = Ftds, Ft – проекция силы на касательную к траектории, направленная в сторону перемещения, или dA = Fdscosa. Если a – острый, то dA>0, тупой – <0, a=90o: dA=0. dA= 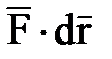 – скалярное произведение вектора силы на вектор элементарного перемещения точки ее приложения; dA= Fxdx+Fydy+Fzdz – аналитическое выражение элементарной работы силы. Единицы работы: – скалярное произведение вектора силы на вектор элементарного перемещения точки ее приложения; dA= Fxdx+Fydy+Fzdz – аналитическое выражение элементарной работы силы. Единицы работы:[1 Дж (джоуль) = 1 Нм]. Элементарная работа силы равна проекции силы на направление перемещения точки , умноженной на элементарное перемещение ds или элементарная работа силы равна произведению модуля силы на элементарное перемещение ds и на косинус угла между направлением силы и направлением перемещения. Мощность. Мощность – величина, определяющая работу в единицу времени, 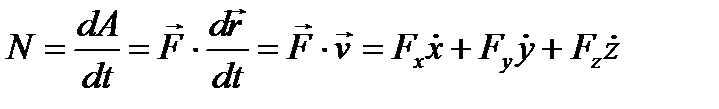 Если изменение работы происходит равномерно, то мощность постоянна: N=A/t. [1 Вт (ватт) =1 Дж/с, 1 кВт (киловатт) = Если изменение работы происходит равномерно, то мощность постоянна: N=A/t. [1 Вт (ватт) =1 Дж/с, 1 кВт (киловатт) == 1000 Вт, 1л.с.(лошадиная сила) = 75 кгс×м/с = 736 Вт] Работа силы на конечном пути. Р-та силы на любом конечном перемещении М0М1: 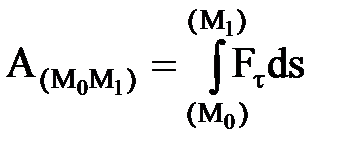 . Если сила постоянна, то . Если сила постоянна, то 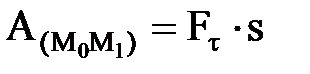 = F×s×cosa.Ед.р-ты:[1 Дж (джоуль) = 1 Нм]. = F×s×cosa.Ед.р-ты:[1 Дж (джоуль) = 1 Нм]. 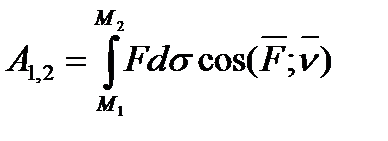 Работа силы тяжести, силы упругости Работа силы тяжести равна взятому со знаком плюс или минус произведению силы тяжести на вертикальное перемещение точки ее приложения (+ перемещение ↓, - перем ↑) A1,2=±GH Работа силы упругости. Работа силы упругости: –работа силы упругости равна половине произведения коэффициента жесткости на разность квадратов начального и конечного удлинений (или сжатий) пружины. 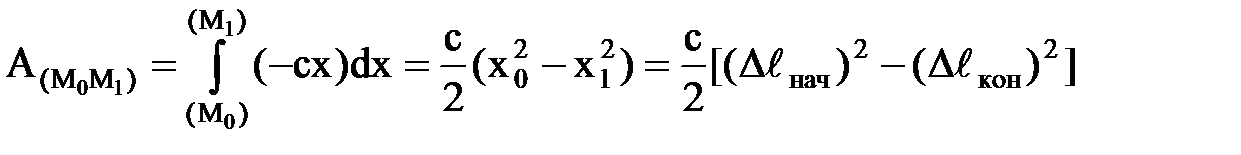 Понятие о силовом поле. Потенциальное силовое поле и силовая функция. Силовым полем называется часть пространства, в каждой точке которого на помещенную туда материальную частицу действует определенная по модулю и направлению сила, зависящая от положения частицы. Функция U от координат x, y, z, дифференциал которой = элементарной работе, называется силовой функцией. Силовое поле, для которого существует силовая функция, называется потенциальным силовым полем, а силы, действующие в этом поле, - потенциальными силами. Потенциальная энергия. Потенциальной энергией материальной точки в данном положении М называется скалярная величина П, равная той работе, которую произведут силы поля при перемещении точки из положения М в нулевое 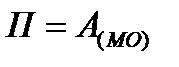 Потенциальная энергия в любой точке силового поля равна значению силовой функции в этой точке, взятому с обратным знаком. Примеры потенциальных силовых полей: однородное поле тяжести. 1)Сила тяжести 2)Сила упругости 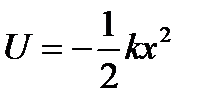 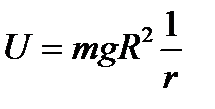 3)Сила тяготения 27 вопрос. Примеры вычисления работы силы. силы тяжести , линейной силы упругости Однородное поле силы тяжести
Рассмотрим материальную точку массой m, находящуюся в однородном поле силы тяжести. Направим ось Oz вертикально вверх, а оси Ox и Oy произвольно в горизонтальной плоскости. Проекции силы тяжести на оси координат будут равны Элементарная работа силы тяжести Так как элементарная работа силы тяжести является полным дифференциалом и 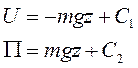 (I) (I)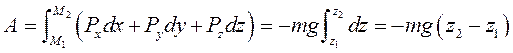 Где А – работа силы тяжести материальной точки массой m на перемещении . (I) можно представить в виде Где - высота подъема точки. Если точка расположена выше , т.е. опускается, то работа положительная, иначе – отрицательная. Поле линейной силы упругости. Лиин. сила упр. подчиняется закону Гука Элементарная работа этой силы: 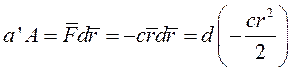 так как 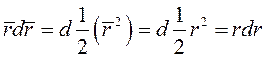 . Интегрируем . Интегрируем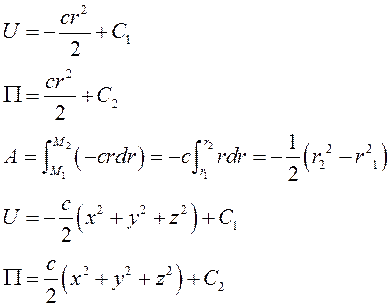 Таким образом, силовая функция и потенциальная энергия линейной силы упругости является квадратичной формой координат точки М, отсчитываемых от положения равновесия. Работа силы упругости не зависит от траектории. При перемещении точки из положения равновесия работа силы упругости отрицательна
Поверхностями уровня линейной упругой силы будут концентрические сферы с центром в начале координат, а силовыми линиями – прямые, проходящие через начало координат, т.к. из 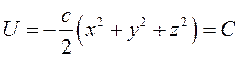 следует 28 вопрос. Работа мощности , приложенных к твердому телу при поступательном, вращательном и свободном движении твердого тела Поступательное движение твердого тела. При поступательном движении твердого тела траектории всех его точек тождественны и параллельны. Поэтому векторы элементарных перемещений геометрически равны. Элементарная работа силы PEi d AEi= PEidr. Для всех сил будет d A=Sd AEi= SPEidr=drSPE=drRE. Следовательно, d A=drRE. (14-46) Элементарная работа сил, приложенных к твердому телу, движущемуся поступательно, равна элементарной работе главного вектора сил. Работа на конечном перемещении А= Элементарная работа сил, приложенных к твердому телу, вращающемуся вокруг неподвижной оси, равна произведению главного момента внешних сил относительно оси вращения на приращение угла поворота. Работа на конечном перемещении SAi= где - главный момент внешних сил относительно оси вращения. Если главный момент постоянен, то SAi= Ez В этом случае сумма работ на конечном перемещении равна произведению главного момента внешних сил на конечное изменение угла поворота тела. Тогда мощность N= В общем случае движения элементарная работа внешних сил, приложенных к свободному твердому телу, равна dA= SdAi= REdrO+ MEWda, (14-51) где MEW - главный момент внешних сил относительно мгновенной оси; da - элементарный угол поворота относительно мгновенной оси. Изменение кинетической энергии механической системы равно алгебраической сумме работ всех внешних и внутренних сил, действующих на эту систему dT = dAвнеш + dAвнутр . (1.55) При вращении твердого тела относительно неподвижной оси элементарная работа всех внешних сил, действующих на твердое тело, равна приращению только кинетической энергии, так как его потенциальная энергия при этом не меняется. Следовательно С учетом того, чтоIzdw = Mzdt ,получим dA = Mzw dt = Mzdj . (1.56) Полная работа внешних сил при повороте твердого тела на некий угол j равна: В случае, если Mz=const, то последнее выражение упрощается: A = Mzj . (1.58) Таким образом,работа внешних сил при вращательном движении твердого тела вокруг неподвижной оси определяется действием момента Mz этих сил относительно данной оси. При вращательном движении твердого тела относительно неподвижной оси мощность определяется выражением ………………………………………………………………………………………………………………………………………. 29 вопрос. |