МЕХАНИКА(1-19). 1. Основные понятия кинематики материальной точки. Описание движения в декартовых координатах. Скорость, нормальное и тангенциальное ускорение при криволинейном движении. Движение материальной точки по окружности. Равномерное и равнопеременное вращение
 Скачать 1 Mb. Скачать 1 Mb.
|
|
1. Основные понятия кинематики материальной точки. Описание движения в декартовых координатах. Скорость, нормальное и тангенциальное ускорение при криволинейном движении. Движение материальной точки по окружности. Равномерное и равнопеременное вращение. Основные понятия: система отсчета, траектория, перемещение. 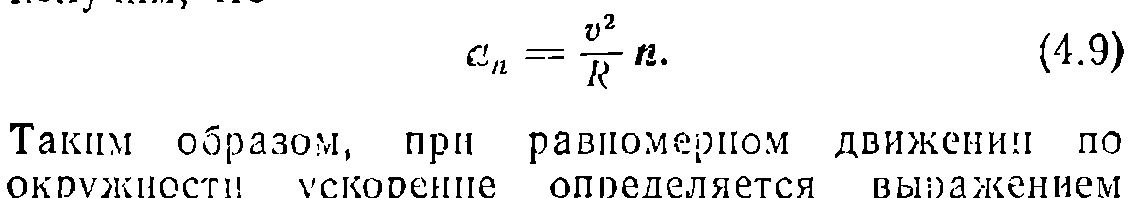 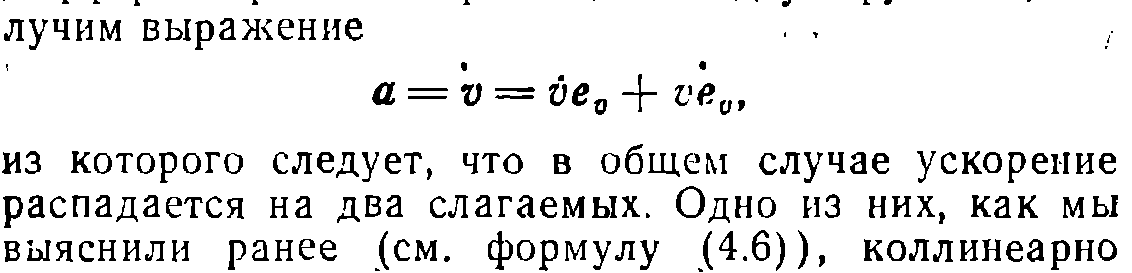  2. Первый закон Ньютона. Инерциальные системы отсчета. Принцип относительности Галилея. Преобразования Галилея. Второй и третий законы Ньютона. Первый закон Ньютона: всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит ее изменить это состояние. Стремление тела сохранять состояние покоя или равномерного прямолинейного движения называется инертностью. Поэтому первый закон Ньютона еще называют законом инерции. Механическое движение относительно, его вид зависит от системы отсчета. Существуют такие системы отчета, в которых ервый закон Ньютона выполняется. Системы, по отношению к которым он выполняется, называются инерциальными системами отсчета. Инерциальной системой отсчета является такая система отсчета, в которой материальная точка, свободная от внешних воздействий, либо остается неподвижной, либо движется равномерно и прямолинейно (т.е. без ускорения). Согласно первому закону Ньютона инерциальные системы отсчета существуют. Опытным путем установлено, что инерциальной можно считать гелиоцентрическую (звездную) систему отсчета (начало координат находится в центре Солнца, а оси проведаны в направлении определенных звезд). Система отсчета, связанная с Землей, строго говоря, неинерциальна, однако эффекты, обусловленные ее неинерциальностью (Земля вращается вокруг собственной оси и вокруг Солнца), при решении многих задач пренебрежимо малы, и в этих случаях ее можно считать инерциальной. второй закон Ньютона: ускорение, приобретаемое материальной точкой (телом), пропорционально вызывающей его силе, совпадает с нею по направлению и обратно пропорционально массе материальной точки (тела). В системе измерений СИ коэффициент пропорциональности k= 1. Тогда или Учитывая, что масса материальной точки (тела) в классической механике постоянна, в выражении (4) массу можно внести под знак производной: Векторная величина численно равная произведению массы материальной точки на ее скорость и имеющая направление скорости, называется импульсом (количеством движения) этой материальной точки.Подставляя (6) в (5), получим Это выражение - более общая формулировка второго закона Ньютона: скорость изменения импульса материальной точки равна действующей на нее силе. Единица силы в СИ - ньютон (Н): 1 Н - сила, которая массе 1 кг сообщает ускорение 1 м/с2 в направлении действия силы: 1 Н = 1 кг•м/с2. Взаимодействие материальных точек (тел) описывается третьим законом Ньютона: всякое действие материальных точек (тел) друг на друга носит характер взаимодействия; силы, с которыми действуют друг на друга материальные точки, всегда равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти точки: F12 = - F21, где F12 - сила, действующая на первую материальную точку со стороны второй; F21 - сила, действующая на вторую материальную точку со стороны первой. Эти силы приложены к разным материальным точкам (телам), всегда действуют парами и являются силами одной природы. ГАЛИЛЕЯ ПРИНЦИП ОТНОСИТЕЛЬНОСТИ в классической механике Ньютона - устанавливает, что во всех инерциальных системах отсчета любой механический процесс протекает одинаково (при одинаковых начальных условиях). 3. Центр масс механической системы. Закон движения центра масс. Движение центра масс замкнутой системы. Закон сохранения импульса.    4. Работа силы и ее выражение через криволинейный интеграл. Мощность. Энергия - универсальная мера различных форм движения и взаимодействия. Различные формы энергии связывают с различными формами движения материи: механическую, тепловую, электромагнитную, ядерную и пр. В одних случаях форма движения материи не изменяется (например, холодное тело нагревает горячее), в других - переходит в другую форму (например, механическое движение превращается в тепловое в результате трения). Однако существенно, что во всех перечисленных случаях энергия, отданная (в той или иной форме) от одного тела другому телу, равна энергии, которую получило последнее тело. Изменение механического движения тела вызывается силами, которые действуют на него со стороны других тел. С целью количественно описать процесс обмена энергией между взаимодействующими телами, в механике вводится понятие работы силы. Если тело движется прямолинейно и на него действует постоянная сила F, составляющая некоторый угол α с направлением перемещения, то работа этой силы равна проекции силы Fs на направление перемещения (Fs= Fcosα), умноженной на соответствующее перемещение точки приложения силы: Но на практике сила может изменяться как по модулю, так и по направлению, поэтому формула (1) непригодна. Однако, если рассмотреть данную ситуацию для элементарного перемещения dr, то силу F мы считаем постоянной, а движение точки ее приложения - прямолинейным. Элементарной работой силы F на перемещении dr называется скалярная величина где α - угол между векторами F и dr; ds = |dr| - элементарный путь; Fs - проекция вектора F на вектор dr (рис. 1). 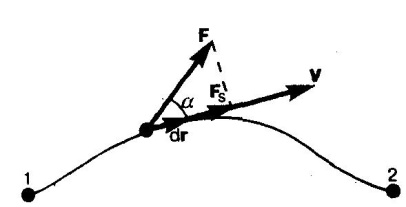 Рис.1 Если взять участок траектории от точки 1 до точки 2, то работа на нем равна алгебраической сумме элементарных работ на отдельных бесконечно малых участках пути. Поэтому эту сумму можно привести к интегралу Чтобы вычислить интеграл (2) надо знать зависимость силы Fs, от пути s вдоль траектории 1-2. Пусть эта зависимость представлена графически (рис. 2), тогда искомая работа А равна на графике площадью заштрихованной фигуры. Если точка движется прямолинейно, сила F=const и α=const, то получим где s - пройденный телом путь (см. также формулу (1)). 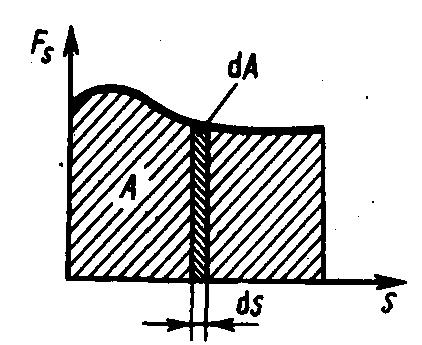 Рис.2 Из формулы (1) следует, что при α<π/2 работа силы положительна, в этом случае составляющая Fs совпадает по направлению с вектором скорости точкиv (см. рис. 1). Если α>π/2, то работа силы отрицательна. При α= π/2 (сила и перемещение перпендикулярны) работа силы равна нулю. Единица работы - джоуль (Дж): 1 Дж - работа, совершаемая силой 1 Н на пути 1 м (1 Дж=1 Н•м). Чтобы охарактеризовать скорость совершения работы, вводят понятие мощности: За время dt сила F совершает работу Fdr, и мощность, развиваемая этой силой, в данный момент времени т. е. равна скалярному произведению вектора силы на вектор скорости, с которой движется точка приложения этой силы; N - величина скалярная. Единица мощности - ватт (Вт): 1 Вт - мощность, при которой за время 1 с совершается работа 1 Дж (1 Вт = 1 Дж/с). 5.Кинетическая энергия системы. Связь изменения кинетической энергии и работы. Кинетическая энергия механической системы - это энергия механического движения рассматриваемой системы. Сила F, воздействуя на покоящееся тело и приводя его в движение, совершает работу, а энергия движущегося тела увеличивается на величину затраченной работы. Значит, работа dA силы F на пути, который тело прошло за время возрастания скорости от 0 до v, тратится на увеличение кинетической энергии dT тела, т. е. Используя второй закон Ньютона Так как v=dr/dt, то dA=mvdv, откуда Таким образом, тело массой m, движущееся со скоростью v, обладает кинетической энергией 6.Консервативные и неконсервативные силы. Сила тяжести, сила упругости, центральные силы как консервативные силы. 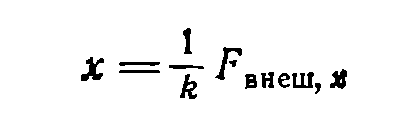 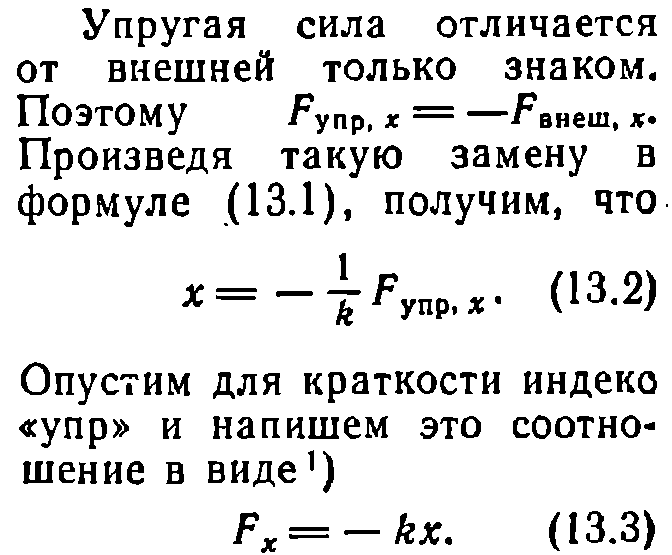 7.Потенциальная энергия материальной точки во внешнем поле. Связь изменения потенциальной энергии и работы. Связь силы, действующей на материальную точку во внешнем поле, с её потенциальной энергией. Полная энергия материальной точки во внешнем поле и её изменение.  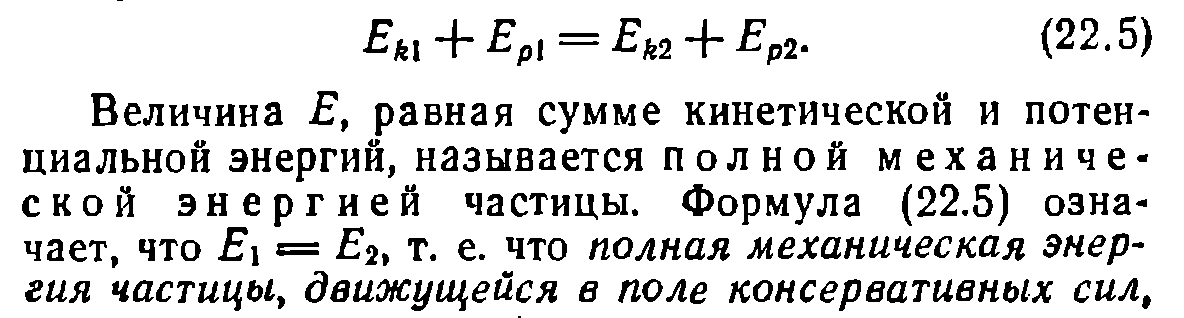 8.полная механическая энергия системы, связь её изменения с работой неконсервативных сил. Закон сохранения полной механической энергии. 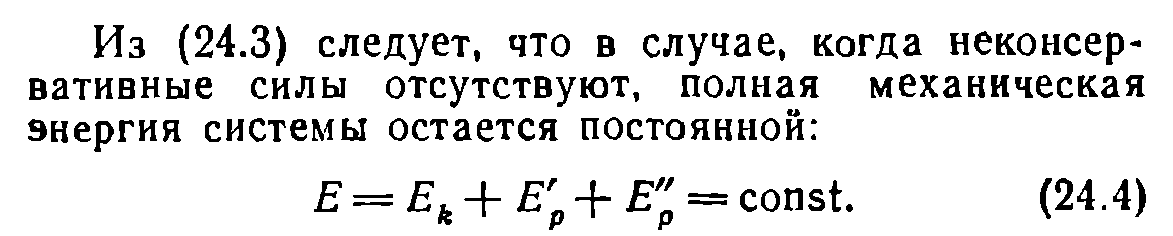  9. Абсолютно неупругий удар. Абсолютно упругий удар. Скорости шаров после абсолютно упругого центрального удара. Абсолютно неупругий удар - соударение двух тел, в результате которого тела соединяются, двигаясь дальше как единое целое. Абсолютно неупругий удар можно продемонстрировать с помощью шаров из пластилина (глины), которые движутся навстречу друг другу . Если массы шаров m1 и m2, их скорости до удара ν1 и ν2, то, используя закон сохранения импульса 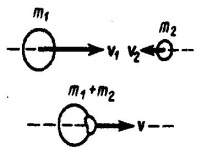 где v - скорость движения шаров после удара. Тогда В случае движения шаров навстречу друг другу они вместе будут продолжать движение в ту сторону, в которую двигался шар с большим импульсом. В частном случае, если массы шаров равны (m1=m2), то Определим, как изменяется кинетическая энергия шаров при центральном абсолютно неупругом ударе. Так как в процессе соударения шаров между ними действуют силы, зависящие от их скоростей, а не от самих деформаций, то мы имеем дело с дисипативными силами, подобным силам трения, поэтому закон сохранения механической энергии в этом случае не должен соблюдаться. Вследствие деформации происходит уменьшение кинетической энергии, которая переходит в тепловую или другие формы энергии. Это уменьшение можно определить по разности кинетической энергии тел до и после удара: Используя (10), получаем Если ударяемое тело было первоначально неподвижно (ν2=0), то и Когда m2>>m1 (масса неподвижного тела очень велика), то ν<<ν1 и практически вся кинетическая энергия тела переходит при ударе в другие формы энергии. Поэтому, например, для получения значительной деформации наковальня должна быть значительно массивнее молота. Наоборот, при забивании гвоздей в стену масса молота должна быть гораздо большей (m1>>m2), тогда ν≈ν1 и почти вся энергия тратится на возможно большее перемещение гвоздя, а не на остаточную деформацию стены. Абсолютно неупругий удар - это пример потери механической энергии под действием диссипативных сил. |
