МЕХАНИКА(1-19). 1. Основные понятия кинематики материальной точки. Описание движения в декартовых координатах. Скорость, нормальное и тангенциальное ускорение при криволинейном движении. Движение материальной точки по окружности. Равномерное и равнопеременное вращение

• Название: 1. Основные понятия кинематики материальной точки. Описание движения в декартовых координатах. Скорость, нормальное и тангенциальное ускорение при криволинейном движении. Движение материальной точки по окружности. Равномерное и равнопеременное вращение
• Анкор: МЕХАНИКА(1-19).docx
• Дата: 07.02.2017
• Размер: 1 Mb.
• Имя файла: МЕХАНИКА(1-19).docx
• Тип: Документы; #2407
• страница: 2 из 4

Абсолютно упругий удар - соударение двух тел, в результате которого в обоих участвующих в столкновении телах не остается никаких деформаций и вся кинетическая энергия тел до удара после удара снова превращается в первоначальную кинетическую энергию (отметим, что это идеализированный случай). 

Для абсолютно упругого удара выполняются закон сохранения кинетической энергии и закон сохранения импульса. 

Обозначим скорости шаров массами m₁ и m₂ до удара через ν₁ и ν₂, после удара - через ν₁' и ν₂' (рис. 1). Для прямого центрального удара векторы скоростей шаров до и после удара лежат на прямой линии, проходящей через их центры. Проекции векторов скоростей на эту линию равны модулям скоростей. Их направления учтем знаками: положительное соотнесем движению вправо, отрицательное - движению влево.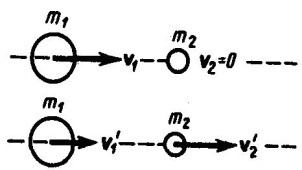 



При указанных допущениях законы сохранения имеют вид 
(1) 
(2) 
Произведя соответствующие преобразования в выражениях (1) и (2), получим 
 (3) 
(4)
откуда 

 (5) 
Решая уравнения (3) и (5), находим 
(6) 

(7) 
Разберем несколько примеров. 
1. При ν₂=0 

(8) 
(9) 
Проанализируем выражения (8) в (9) для двух шаров различных масс: 
а) m₁=m₂. Если второй шар до удара висел неподвижно (ν₂=0) (рис. 2), то после удара остановится первый шар (ν₁'=0), а второй будет двигаться с той же скоростью и в том же направлении, в котором двигался первый шар до удара (ν₂'=ν₁);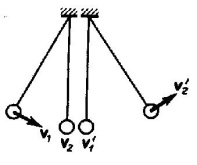



б) m₁>m₂. Первый шар продолжает двигаться в том же направлении, как и до удара, но с меньшей скоростью (ν₁'<ν₁). Скорость второго шара после удара больше, чем скорость первого после удара (ν₂'>ν₁' ) (рис. 3);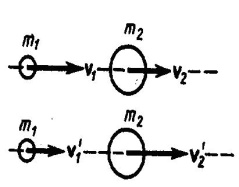



в) m₁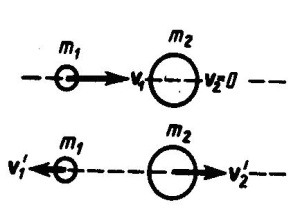₂. При ударе направление движения первого шара изменяется - шар отскакивает обратно. При этом второй шар движется в сторону, в которую двигался первый шар до удара, но с меньшей скоростью, т. е. ν₂'<ν₁ (рис. 4);



г) m₂>>m₁ (например, столкновение шара со стеной). Из уравнений (8) и (9) следует, что ν₁'= -ν₁; ν₂' ≈ 2m₁ν₂'/m₂. 
2. При m₁=m₂ выражения (6) и (7) будут иметь вид ν₁'= ν₂; ν₂'= ν₁; т. е. шары равной массы как бы обмениваются скоростями. 
10.Момент импульса частицы относительно точки и относительно оси. Момент силы относительно точки и относительно оси. Законы изменения и сохранения момента импульс системы. Момент импульса твердого тела, вращающегося относительно неподвижной оси. Момент инерции тела относительно оси. Вычисление моментов инерции стержня, сплошного цилиндра. Теорема Гюйгенса-Штейнера. Закон сохранения момента импульса для вращательного движения.

Моментом импульса (количества движения) материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением: 

 

где r - радиус-вектор, проведенный из точки О в точку A, p=mv - импульс материальной точки (рис. 1); L - псевдовектор, направление которого совпадает с направлением поступательного движения правого винта при его вращении от r к р.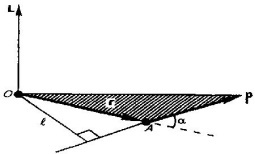



Модуль вектора момента импульса 

 

где α - угол между векторами r и р, l - плечо вектора р относительно точки О. 

Моментом импульса относительно неподвижной оси z называется скалярная величина L_z, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси. Момент импульса L_z не зависит от положения точки О на оси z. 

При вращении абсолютно твердого тела вокруг неподвижной оси z каждая точка тела движется по окружности постоянного радиуса r_iсо скоростью v_i . Скорость v_i и импульс m_iv_i перпендикулярны этому радиусу, т. е. радиус является плечом вектора m_iv_i . Значит, мы можем записать, что момент импульса отдельной частицы равен 

(1) 

и направлен по оси в сторону, определяемую правилом правого винта. 

Монет импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц: 

 

Используя формулу v_i = ωr_i, получим 

 

т. е.  2) 

Таким образом, момент импульса твердого тела относительно оси равен моменту инерции тела относительно той же оси, умноженному на угловую скорость. Продифференцируем уравнение (2) по времени: 

 

т. е. 

 

Эта формула - еще одна форма уравнения динамики вращательного движения твердого тела относительно неподвижной оси: производная момента импульса твердого тела относительно оси равна моменту сил относительно той же оси. 

Можно показать, что имеет место векторное равенство 

(3) 
В замкнутой системе момент внешних сил  и  откуда 

 (4) 

Выражение (4) представляет собой закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т. е. не изменяется с течением времени. 

Закон сохранения момента импульса также как и закон сохранения энергии является фундаментальным законом природы. Он связан со свойством симметрии пространства - его изотропностью, т. е. с инвариантностью физических законов относительно выбора направления осей координат системы отсчета (относительно поворота замкнутой системы в пространстве на любой угол). 

Здесь мы продемонстрируем закон сохранения момента импульса с помощью скамьи Жуковского. Человек, сидящий на скамье, вращающаяся вокруг вертикальной оси, и держащий в вытянутых руках гантели (рис. 2), вращается внешним механизмом с угловой скоростью ω₁. Если человек прижмет гантели к телу, то момент инерции системы уменьшится. Но момент внешних сил равен нулю, момент импульса системы сохраняется и угловая скорость вращения ω₂ увеличивается. Аналогичным образом, гимнаст во время прыжка через голову поджимает к туловищу руки и ноги, с целью уменьшить свой момент инерции и тем самым увеличить угловую скорость вращения. 
Сопоставим основные величины и уравнения, определяющие вращение тела вокруг неподвижной оси и его поступательное движение (см таблицы ниже).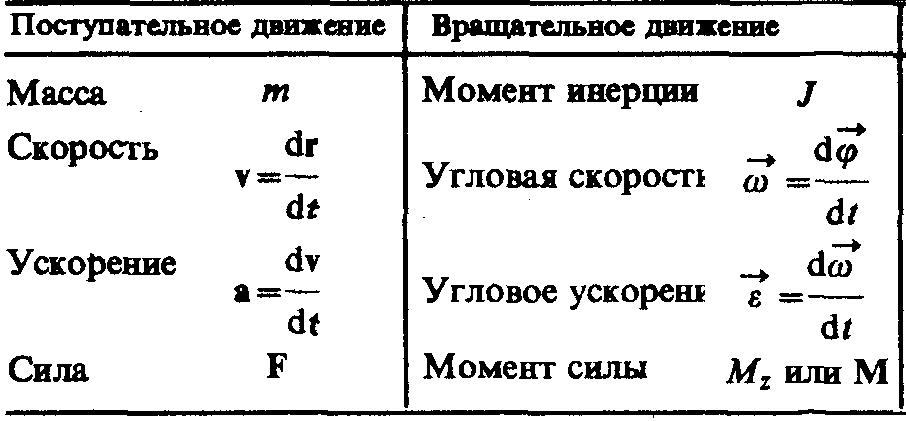






Моментом силыFотносительно неподвижной точки О называется физическая величина, определяемая векторным произведением радиуса-вектора r, проведенного из точки О в точку А приложения силы, на силу F (рис. 1):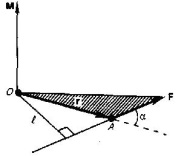 



 

Здесь М - псевдовектор, направление которого совпадает с направлением поступательного движения правого винта при его вращении от r к F. Модуль момента силы 

 (1) 

где α - угол между r и F; rsinα=l - наименьшее расстояние между линией действия силы и точкой О - плечо силы. 

Моментом силы относительно неподвижной оси z называется скалярная величина M_z , равная проекции на эту ось вектора М момента силы, определенного относительно произвольной точки О данной оси z (р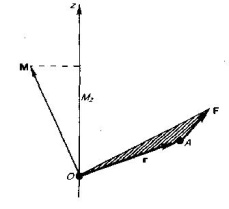ис. 2). 
Рис.2

Значение момента М_z не зависит от выбора положения точки О на оси z. 
Если ось z совпадает с направлением вектора М, то момент силы представляется в виде вектора, совпадающего с осью: 

 

Найдем выражение для работы при вращении тела (р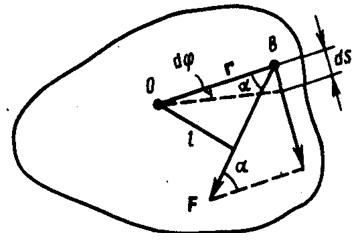ис.3). 
Рис.3

Пусть сила F приложена в точке В, находящейся от оси z на расстоянии r, α - угол между радиусом-вектором r и направлением силы. Так как тело абсолютно твердое, то работа этой силы равна работе, которую необходимо затратить на поворот всего тела. При повороте тела на бесконечно малый угол dφ точка приложения В проходит путь ds=rdφ и работа равна произведению проекции силы на направление с мещения на величину смещения: 

(2) 

Учитывая (1), можем записать 

 

где Frsinα=Fl=M_z - момент силы относительно оси z. Значит, работа при вращении тела равна произведению момента действующей силы на угол поворота. 
Работа при вращении тела идет на увеличение его кинетической энергии: dA=dT, но  поэтому , или  
Учитывая, что  получаем 

 (3) 

Уравнение (3) представляет собой уравнение динамики вращательного движения твердого тела относительно неподвижной оси. 
Можно показать, что если ось z совпадает с главной осью инерции, проходящей через центр масс, то имеет место векторное равенство 

 

где J - главный момент инерции тела (момент инерции относительно главной оси).