Алгоритмы компьютерной графики Пешков Анатолий Тимофеевич, БГУИР. 1 отображение просранства пользователя и машинного носителя 4

• Название: 1 отображение просранства пользователя и машинного носителя 4
• Дата: 24.09.2022
• Размер: 1.86 Mb.
• Имя файла: Алгоритмы компьютерной графики Пешков Анатолий Тимофеевич, БГУИР.doc
• Тип: Документы; #693275
• страница: 6 из 20

3 ДВУМЕРНОЕ ОТСЕЧЕНИЕ

Задача отсечения весьма часто встречается в машинной графике, например, при затенении объектов заднего плана объектами переднего плана, при работе с пользовательскими окнами и т.п.

3.1 Отсечение прямоугольным окном. Алгоритм Сазерленда-Коуэна.

В рассматриваемом отсечении окно представляет собой прямоугольник, стороны которого параллельны осям координат, как это показано на приведенном рисунке (Рис. Отсечение выпуклым многоугольным окном. Алгоритм Кируса-Бэка-26).

При внутреннем отсечении отображаются только те фрагменты отсекаемой фигуры, которые попадают во внутреннюю область окна, а все остальные отбрасываются. Для приведенного на рисунке окна у треугольника АВС отбрасывается часть Bp₁p₂ и треугольник отображается своей частью АР₁Р₂С.

При внешнем отсечении отображается лишь то, что оказывается вне окна.

Определить отображаемую часть отсекаемой фигуры, можно, если будут известны точки пересечения ее ребер со сторонами заданного окна. Поэтому задача отсечения окном в конечном случае сводится к задаче отсечения отрезка.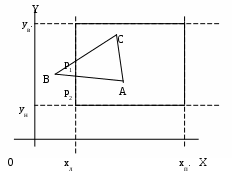



Рис. Отсечение прямоугольным окном. Алгоритм Сазерленда-Коуэна.‑18
Прямоугольное окно задается четырьмя параметрами x_л,x_п,y_н,y_в, соответственно, левой, правой, нижней и верхней границами (ребрми).

Математически задача довольно-таки проста: нужно найти точки пересечения отсекаемого отрезка со сторонами окна.

Пересечение отрезка, заданного начальной Н(x_н,y_н) и конечной К(x_к,y_к) точками, с вертикальной (например, левой) стороной ищется следующим образом (Error: Reference source not found а), где точка пересечения обозначена как «П»):
x_п = x_л,

(y_п - y_Н)/(y_к- y_Н) = (x_л – x_Н)/(x_к – x_Н), откуда:

y_п = y_Н+ (x_л –x_Н) m, где крутизна отрезка m = (y_к- y_Н)/(x_к – x_Н).
Пересечение этого отрезка с горизонтальной (например, верхней) стороной ищется как:
y_п = y_в,

(x_п - x_Н)/(x_к - x_Н) = (y_в – y_Н)/(y_к – y_Н), откуда:

x_п = x_Н + (y_в – y_Н)(1/m).
Таким образом будет найдена точка пересечения прямых, несущих заданный отрезок и текущую сторону прямоугольного окна. Далее необходимо определить принадлежность этой точки одновременно и заданному отрезку и соответствующей стороне окна. Эта процедура должна быть выполнена для всех четырех сторон окна, что требует больших затрат времени.

Количество отсекаемых отрезков, в общем случае, может быть достаточно велико, большинство из которых вообще может не иметь пересечение со сторонами окна. В этот связи интерес представляет алгоритм Сазерленда-Коуэна, обеспечивающий поиск точек пересечения только для ограниченного числа отрезков, видимость которых не очевидна.

Для быстрого анализа видимости отрезка в этом алгоритме используется кодирование концов отрезка. Для этого пространство, в котором находится окно, разбивается на девять областей, как это показано на рисунке (Рис. Отсечение прямоугольным окном. Алгоритм Сазерленда-Коуэна.-19).

Каждой области приписывается четырех разрядный код, причем первый разряд определяет положение области по отношению к линии, несущей левую сторону окна, второй разряд определяет положение области по отношению к линии, несущей правую сторону окна, третий разряд определяет положение области по отношению к линии, несущей нижнюю сторону окна, четвертый разряд определяет положение области по отношению к линии, несущей верхнею сторону окна. При этом принимается, что каждая линия, несущая сторону окна, разбивает все пространство на две области внутреннюю, в которой располагается окно, и противоположную внешнюю.

Если точка лежит по отношению к некоторой стороны окна во внутренней области, то в соответствующий разряд четырех битового кода устанавливается ноль, в противном случае в этот разряд устанавливается единица. При кодировании концевым точкам приписывается код области, в которой они находится. Например, на Рис. Отсечение прямоугольным окном. Алгоритм Сазерленда-Коуэна.-19а) точка А по отношению к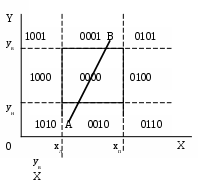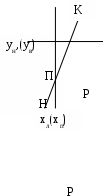






а) в)

Рис. Отсечение прямоугольным окном. Алгоритм Сазерленда-Коуэна.‑19
левой стороне окна располагается во внутренней области, поэтому первый разряд четырех битового кода равен 0, второй разряд этого кода равен нулю, так как точка А располагается во внутренней области по отношению к правой стороне окна, третий разряд этого кода равен единицы, так как точка А располагается во внешней области по отношению к нижней стороны окна, четвертый разряд кода равен нулю, так как точка А располагается во внутренней области по отношению к верхней стороне окна.

Используя описанную кодировку, можно утверждать, что полностью видимый отрезок должен имеет нулевые коды для обоих своих концов. С другой стороны, если оба конца отрезка располагаются с внешней стороны по отношению хотя бы одной стороны окна, то он полностью невидим. Обращает на себя внимание тот факт, что логическое произведение кодов концов отрезка в этом случае будет отлично от нуля.

На Рис. Отсечение прямоугольным окном. Алгоритм Сазерленда-Коуэна.-20 а) приведено несколько отрезков, расположенных в пространстве с окном, а на Рис. Отсечение прямоугольным окном. Алгоритм Сазерленда-Коуэна.-20 b) приведены в виде таблицы кодировка концов всех имеющихся отрезков и результаты анализа их видимости.

Идея алгоритма Сазерленда-Коуэна заключается в следующем.

Сначала кодируются концы отрезка и проверяется наличие его явной видимости (отрезок полностью видим или очевидно не видим). Если признаков явной видимости нет, то поочередно ищется пересечение отрезка с линией, несущей одно из ребер окна. При этом перед поиском пересечения отрезок ориентируется таким образом, чтобы его начало находилось с внешней стороны относительно линии, несущей текущую сторону (ребро). Пересечение ищется только в том случае, когда концы отрезка располагаются по разные стороны от текущего ребра окна.

Если оба конца отрезка находятся с внутренней стороны от рассматриваемой линии, то осуществляется переход к следующему ребру окна.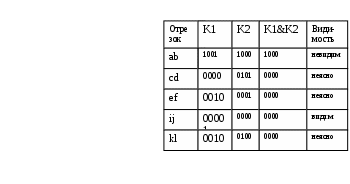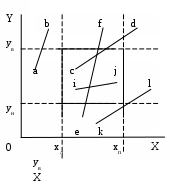



Рис. Отсечение прямоугольным окном. Алгоритм Сазерленда-Коуэна.‑20

Если точка пересечения найдена, то начало отрезка перемещается в эту точку, точка нового начала отрезка кодируется и осуществляется анализ наличия очевидной видимости полученного нового отрезка. Если видимость отрезка не очевидна, то процедура повторяется для очередного ребра окна и т.д.

В крайнем случае, после выполнения описанной процедуры для последнего ребра обязательно будет иметь место случай очевидной видимости. При обнаружении очевидной видимости отрезок будет или полностью невидим, или полностью видим и задача считается решенной.

На следующем рисунке(Рис. Отсечение прямоугольным окном. Алгоритм Сазерленда-Коуэна.-21) приведена последовательность операций с отрезком.




Рис. Отсечение прямоугольным окном. Алгоритм Сазерленда-Коуэна.‑21
На приведенном рисунке в исходном задании положение начальной Р_н, и конечной Р_к точек таково, что принимается решение о неочевидной видимости отрезка. Поэтому запускается процедура поиск его пересечения с ребрами окна, начиная с левого.

С линией, несущей левое ребро, отрезок не пересекается, поэтому осуществляется переход к следующему правому ребру.

Отрезок пересекается с линией, несущей правое ребро, но его начало располагается с внутренней стороны от этого ребра, поэтому начало и конец отрезка меняются местами и ищется пересечение линии, несущей отрезок Р_н1, Р_к1 и линии, несущей правое ребро окна. Начало отрезка переносится в найденную точку пересечения.

Вновь полученный отрезок Р_н2, Р _к2 имеет неочевидную видимость, поэтому осуществляется переход к определению пересечения отрезка с очередным (нижним) ребром. Начало и конец меняются местами и для вновь образованного отрезка Р_н3, Р _к3 находится точка его пересечения с нижним ребром. В эту точку переносится начало отрезка и анализируется видимость вновь полученного отрезка Р_н4, Р _к4 .

Отрезок Р_н4, Р_к4 будет полностью видим, задача считается решенной и часть Р_н4, Р_к4 исходного отрезка Р_н, Р_к отображается на носителе.

Граф-схема алгоритма Сазерленда-Коуэна приведена на (Рис. Отсечение прямоугольным окном. Алгоритм Сазерленда-Коуэна.-22 иРис. Отсечение прямоугольным окном. Алгоритм Сазерленда-Коуэна.-23).

На граф-схеме приняты следующие обозначения.

• 
  P_н, P_к – двух элементная матрица координат начальной и конечной точек отрезка, нулевые элементы которых содержит координаты X, а первые элементы – координаты Y конечных точек;
  
• 
  О – четырех элементная матрица, задающее положение отсекающего окна, причем в ее нулевом, первом, втором и третьем элементах, располагаются координаты, определяющие положение, соответственно, левого, правого, нижнего и верхнего ребер заданного окна;
  
• 
  K_н, K_к – четырех элементные бинарные матрицы, содержащие коды точек, соответственно, конца и начала отрезка, причем в их нулевом,
  

первом, втором и третьем элементах, располагаются биты, определяющие положение кодируемой точки по отношений к, соответственно, левому, правому, нижнему и верхнему реберам заданного окна;

• 
  J – номер текущего ребра заданного окна;
  
• 
  В – функция очевидной видимости отрезка, которой может быть приписано одно из трех значений:
  

• 
  1 – если отрезок полностью видим;
  
• 
  0- если отрезок полностью невидим;
  
• 
  2 – если видимость отрезка неочевидна;
  

Рис. Отсечение прямоугольным окном. Алгоритм Сазерленда-Коуэна.‑22

• 
  F – переменная, определяющая вид отрезка, которая приписывается значение «1», если отрезок вертикальный, и «0» во всех остальных случаях;
  
• 
  m - крутизна отрезка.
  

Рис. Отсечение прямоугольным окном. Алгоритм Сазерленда-Коуэна.‑23
Блок операторов 1 граф–схемы выполняет кодировку концов отрезка (подпрограммы Rut1) и определяет переменную очевидной видимости B (подпрограммы Rut2).

Блок 2 на основании значения В или отображает отрезок, или заканчивает задачу (отрезок очевидно видим или очевидно не видим), или переходит к процессу поиска пересечения отрезка с очередного ребром j с предварительно сориентированным отрезком.

Блок 3 реализует задачу определения крутизны отрезка перед определением пересечения с левым ребром.

Блок 4 осуществляет расчет точки пересечения для вертикальных ребер окна.

Блок 5 осуществляет расчет точки пересечения для горизонтальных ребер окна.

Блок 6 отображает отрезок или его видимую часть и завершает решение задачи.

На Рис. Отсечение прямоугольным окном. Алгоритм Сазерленда-Коуэна.-24 приведена граф-схема подпрограммы Rut1(j,O,P;K), обеспечивающей формирование четырех битового кода K1 для точки P, в зависимости от параметров окна, параметры которые заданы матрицей О.

Входными параметрами данной подпрограммы являются параметры окна (четырех элементная матрица О), матриц координат кодируемой точки, и номер ребра j окна, начиная с которого будет выполняться кодировка. На выходе подпрограмма формирует элементы бинарной матрицы кода заданной точки.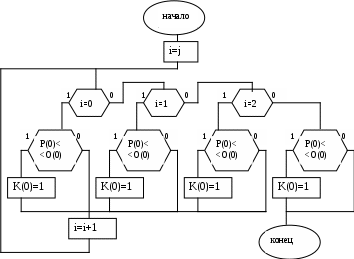



Рис. Отсечение прямоугольным окном. Алгоритм Сазерленда-Коуэна.‑24
В алгоритме, приведенном наРис. Отсечение прямоугольным окном. Алгоритм Сазерленда-Коуэна.-22, на первую подпрограмму Rut1(j,O,P;K) подается матрица координат конечной точки отрезка, а сформированный ею код используется как код конца отрезка.

На вторую подпрограмму Rut1(j,O,P;K) подается матрица координат начальной точки отрезка, а сформированный ею код используется как код начала отрезка.

На Рис. Отсечение прямоугольным окном. Алгоритм Сазерленда-Коуэна.-25 приведена граф-схема подпрограммы Rut2(K_н,К_к;В), обеспечивающей на основании кодов К_н, К_к формирование значение для функции В видимости этого отрезка.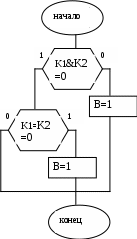



Рис. Отсечение прямоугольным окном. Алгоритм Сазерленда-Коуэна.‑25