ответы к экзамену. 1. Понитие nмерного вектора, основные определения

• Название: 1. Понитие nмерного вектора, основные определения
• Анкор: ответы к экзамену.doc
• Дата: 17.12.2017
• Размер: 8.76 Mb.
• Имя файла: ответы к экзамену.doc
• Тип: Документы; #11906
• страница: 3 из 3

Теорема

Разрешенная система уравнений всегда совместна (потому что она имеет хотя бы одно решение); причем если система не имеет свободных неизвестных, (то есть в системе уравнений все разрешенные входят в базис) то она определена (имеет единственное решение); если же имеется хотя бы одна свободная переменная, то система не определена (имеет бесконечное множество решений).
15.Однородные системы линейных уравнений

Определение 22. Система линейных уравнений называется однородной, если во всех ее уравнениях свободные члены равны нулю.

В общем случае однородная система (или система однородных уравнений) имеет вид

{a11x1+a12x2+...+a1nxn=0

{a21x1+a22x2+...+a2nxn=0

{…............................

{am1x1+am2x2+...+amnxn=0

Однородная система уравнений всегда совместна: действительно, набор значений неизвестных хi = 0 (i = l, 2, ...,n) удовлетворяет всем уравнениям системы. Это решение однородной системы называется нулевым, или тривиальным.

Решение системы однородных уравнений

Вопрос о существовании ненулевого решения однородной системы линейных уравнений (1.53) разрешает следующая теорема.

Теорема 1.7. Однородная система имеет ненулевое решение тогда и только тогда, когда ранг этой системы меньше числа ее неизвестных.

Из этой теоремы вытекают два важных следствия.

1. Если число уравнений однородной системы меньше числа ее неизвестных, то эта система имеет ненулевое решение.

2. 
   Если в однородной системе число уравнений равно числу неизвестных, то она имеет ненулевое решение тогда и только тогда, когда
   

определитель матрицы системы равен нулю.

Теорема. Для того, чтобы однородная система была нетривиально совместна, необходимо и достаточно, чтобы ранг r матрицы системы был меньше числа неизвестных n.

16.Необходимое и достаточное условие существования нетривиального решения системы nxm:

Если однородная система имеет единственное решение, то это единственное решение — нулевое, и система называется тривиально совместной.Если же однородная система имеет более одного решения, то среди этих решений есть и ненулевые и в этом случае система называется нетривиально совместной. При m=n для нетривиальной совместности системы необходимо и достаточно, чтобы определитель матрицы системы был равен нулю.

Теорема. Для того, чтобы однородная система была нетривиально совместна, необходимо и достаточно, чтобы ранг r матрицы системы был меньше числа неизвестных n.
17. Фундаментальная система решений

Решения однородной системы обладают следующими свойствами, если вектор α =(α1, α2, …,αn ) является решением системы (1.53), то и для любого числа k вектор kα =(kα1 kα2, ..., kαn)также будет решением этой системы. Если решением системы (1.53) является также и вектор γ =(γ1, γ2, …, γn), то сумма α+γ также будет решением

этой системы. Отсюда следует, что любая линейная комбинация решений однородной системы также является решением этой системы.

Как мы знаем из 1.1.4, всякая система n-мерных векторов, состоящая более чем из n векторов, является линейно зависимой. Таким образом, из множества векторов-решений однородной системы (1.53) можно

выбрать базис, т. е. любой вектор-решение данной системы будет линейной комбинацией векторов этого базиса. Любой такой базис называется фундаментальной системой решений (ФСР) однородной системы линейных уравнений. Справедлива следующая теорема.

Теорема 1.8. Если ранг r системы однородных уравнений (1.53) мень-ше числа неизвестных п, то всякая ее фундаментальная система решений состоит из (n - r) решений.

Укажем теперь способ нахождения фундаментальной системы решений. Пусть система однородных уравнений (1.53) имеет ранг г < n. Тогда, как следует из правила Крамера, базисные неизвестные этой системы Х1, х2, ..., хг линейно выражаются через свободные переменные

xr+1, …, xn:

x1=β11x1+β12x2+...+β1n-rxn

…..............................................

xr=βr1xr+1 + βr2xr+2 + … + βrn-rxn

Выделим частные решения однородной системы (1.53) по следующему принципу. Для нахождения первого вектора-решения х, примем значения свободных переменных xr+1=1, xr+2=xr+3=xn=0. Затем

находим второе решение х2: принимаем х,.+ 2 = 1, а остальные г - 1 свободные переменные примем равными нулю. Иными словами, мы последовательно присваиваем каждой свободной переменной единичное

значение, считая остальные нулями. Таким образом, фундаментальная система решений (ФСР) в векторной форме с учетом первых г базисных переменных (1.54) имеет вид

x1 = (β11, β21, …, βr1, 1, 0, ...0) ,

х2 = (β12, β22, …, βr2, 0, 1, 0, …, 0 ),

…...........................................................................................

xn-1=(β1n-r, β2n-r, …, βr n-r, 0, …, 0, 1)

(1.55)

Фундаментальная система решений (1.55) является одним из фундаментальных наборов решений однородной системы (1.53).
18.Общее решение системы уравнений в векторной форме:

В общем случае система линейных уравнений, содержащая m уравнений и n уравнений имеет вид: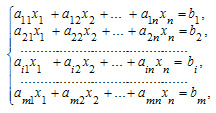



где, a_ij (i=1,2,...,m; j=1,2,...,n) и b_i (i=1,2,...,m), постоянные величины.

Решением системы уравнений называется такой n-мерный вектор Х = (x₁, x₂,...,x_n), который одновременно является решением каждого из уравнений системы.

Общее решение системы уравнений можно записать в векторной форме:
A₁x₁ + A₂x₂ + ... + A_nx_n =B



Пример 1. Записать в векторном виде.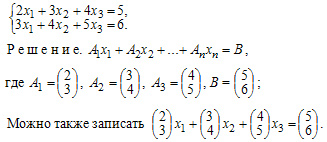



19.Собственные значения и собственные векторы матрицы:

Определение: Число λ называется собственным значени­ем матрицы А порядка п, если существует такой ненулевой вектор Rⁿ, что выполняется равенство

При этом вектор называется собственным вектором матрицы А, а λ — собственным значением матрицы А, соответствую­щим вектору .

Иными словами, умножение матрицы на ее собственный вектор равносильно удлинению этого вектора в |λ| раз, если |λ| > 1. Если λ = 1, умножение мат­рицы на соответствующий собственный вектор не меняет его. Уравнение (13.5) представлено в матричной форме. Группируя все слагаемые этого уравнения в левой части, перепишем его в более удобном виде:

где Е и — соответственно единичная матрица и нулевой век­тор.

Если a_ij — элементы матрицы А, то характеристическая матрица А — λЕ, согласно определениям умножения матрицы на число и суммы матриц, имеет вид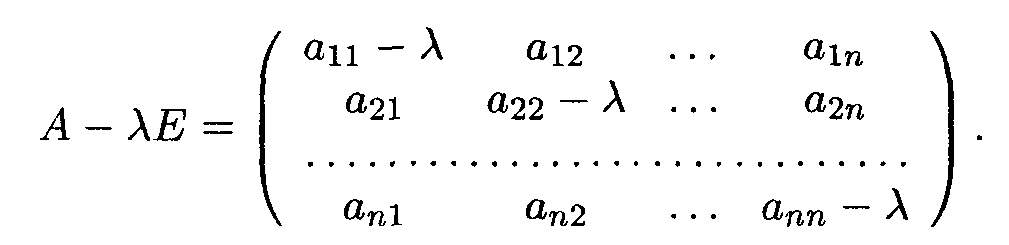


20. Ортогональная и ортонормированная система векторов.




21. Ортогонализация системы векторов.

Рассмотрим базис пространства R", в котором каждый вектор ортогонален остальным векторам базиса:

ē1, ē2, ..., ēn; ējēi=0, i≠j; i, j = 1,2,...,n.

Ортогональные базисы известны и хорошо представимы на плоскости и в пространстве. Базисы такого вида удобны прежде всего тем, что координаты разложения произвольного вектора определяются по весьма простой процедуре, без применения трудоемких вычислений.1.2. Матрицы 19

Действительно, пусть требуется найти разложение произвольного вектора b в ортогональном базисе (1.15). Составим разложение этого вектора с неизвестными пока координатами разложения в данном базисе:

_

b=a1ē1+a2ē+...+anēn

Умножим обе части этого равенства, представляющие собой векторы, на вектор е,. В силу свойств 2 и 3 скалярного произведения векторов имеем

_

bē, = α1(ē1ēi)+α2(ē2ēi)+...+αi(ēiēi)+αn(ēnēi)

Однако в силу взаимной ортогональности векторов базиса (1.15) все скалярные произведения векторов базиса, за исключением г'-го, равны нулю, т. е. коэффициенты а, определяется по формуле

_ _

α1=(bēi)/(ēiēi)=(bēi)/|ēi|^2; i=1, 2, ..., n

Отметим особо частный случай ортогонального базиса, когда все векторы в (1.15) имеют единичную длину (|ё,. | =1) или нормированы по своей длине. В таком случае базис называют ортопормированным и координаты разложения (1.17) имеют наиболее простой вид:

_

α1= bēi, i=1, 2, ..., n
22. Собственные векторы симметричной матрицы. построение ортонормированного базиса.

Определение 14. Число X называется собственным значением матрицы А порядка п, если существует такой ненулевой вектор х е R", что выполняется равенство

Ах = Хх. (1.26)

При этом вектор х называется собственным вектором матрицы А, аХ — собственным значением матрицы А, соответствующим вектору х.

Уравнение (1.26) представлено в матричной форме. Группируя все слагаемые этого уравнения в левой части, его можно переписать в более удобном виде:

(А-ХЕ)х = 0. (1.27)

Проблема отыскания собственных значений и собственных векторов матриц составляет основу специального раздела алгебры — далее мы еще вернемся к этому вопросу. Здесь лишь отметим один важный результат алгебры матриц: для симметрических матриц (1.23) все п собственных значений являются действительными числами.





23.





24. Ортогональные матрицы. Построение ортогональной матрицы:

Любую матрицу, состоящую из попарно ортогональных нормированных столбцов, можно дополнить до ортогональной матрицы. Действительно, столбцов в такой матрице не может быть больше n. Если их n, то матрица ортогональна. Если же их меньше n, то можно присоединять новые столбцы до тех пор, пока не придем к ортогональной матрице.

25. Понятие квадратичной формы. Стандартный и канонический виды квадратичной формы:






26.

Приведение квадратичной формы к каноническому виду:



Затем полный квадрат при х2 и невыраженное линейное преобразование (у1=.., у2=.., у3=...)


27. Общая постановка задачи математического програмирования.


28. ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

В настоящее время в литературе насчитывается несколько десятков определений понятия "модель", отличающихся друг от друга.

Тем не менее это понятие знакомо каждому: например, игрушечный самолет, бумажный голубь — модели самолета. Менее привычно представление о том, что фотоснимок пейзажа, географическая карта

— это модель местности. И, наверное, новым для многих является

то, что знакомая со школьных лет формула пути s = vt — математическая модель. Под моделью будем понимать условный образ какого-либо объекта, приближенно воссоздающий этот объект с помощью не-

которого языка. В экономико-математических моделях таким объектом является экономический процесс (например, использование ресурсов, распределение изделий между различными типами обору-

дования и т.п.), а языко м — классические и специально разработанные математические методы.

Экономико-математическая модель — математическое описание исследуемого экономического процесса или объекта. Эта модель выражает закономерности экономического процесса в абстрактном виде

с помощью математических соотношений. Использование математического моделирования в экономике позволяет углубить количественный экономический анализ, расширить область экономической информации, интенсифицировать экономические расчеты.

Можно выделить три основных этапа проведения экономикоматематического моделирования. На п е р в о м этапе ставятся цели и задачи исследования, проводится качественное описание объекта в

виде экономической модели. На втором этапе формируется математическая модель изучаемого объекта, осуществляется выбор (или разработка) методов исследования, проводится программирование

модели на ЭВМ, подготавливается исходная информация. Далее проверяются пригодность машинной модели на основании правильности получаемых с ее помощью результатов и оценка их устойчивости.

На третьем, основном, этапе экономико-математического моделирования осуществляются анализ математической модели, реализованной в виде программ для ЭВМ, проведение машинных расчетов,

обработка и анализ полученных результатов.

Процедура экономико-математического моделирования заменяет дорогостоящие и трудоемкие натуральные эксперименты расчетами. Действительно, при использовании экономико-ма-

тематических методов достаточно быстро и дешево производится на ЭВМ сравнение многочисленных вариантов планов и управленческих решений. В результате отбираются наиболее оптимальные варианты.

Ниже рассматриваются примеры экономико-математических моделей.
29.

Стандартная и каноническая формы записи ЗЛП. Правила, позволяющие осуществлять эквивалентные перезаписи задачи:

Если система ограничений состоит лишь из одних неравенств, то такая система программирования – стандартная. Если она состоит из уравнений – каноническая. Вне зависимости от того как записана задача, она может быть переписана в любой форме. Существует Правила, позволяющие осуществлять эквивалентные перезаписи задачи

1) обеспечить нужную оптимизацию цели задачи возможно с помощью умножения исходной функции на (-1). F(x)→min. -F(x)→max

2) Любое неравенство можно умножить на (-1) и перейти к неравенству другого знака

3) ограничение равенства всегда можно записать в виде системы двух неравенств

4) от ограничений неравенств можно перейти к равенствам, добавляя или отнимая неотрицательные новые переменные (доп. переменные)

5) чтобы обеспечить условия неотрицательности переменных можно: любое число всегда можно представить в виде разности двух чисел. Если в задаче присутствует требование, что , то делается замена
30.

Графическая интерпретация ЗЛП:

Если система ограничений ЗЛП представлена в виде системы линейных неравенств с двумя переменными, то задача может быть решена геометрически. Т.о., данный метод ЗЛП имеет очень узкие рамки применения. Геометрический метод предполагает последовательное выполнение ряда шагов:

1) Сформулировать ЗЛП

2) Построить на плоскости прямые, уравнения которых получаются в результате замены в ограничениях знаков неравенств на знаки равенств.

3)Найти полуплоскости, определяемые каждым из ограничений задачи. (пересечение полуплоскостей образуют многогранник решений)

4) найти область допустимых решений.

5) построение уровней целевой функции (построение grad)

6) перемещать прямую, перпендикулярную прямой grad для поиска max или min целевой функции

7) Определить координаты точки максимума (минимума) функции и вычислить значение функции в этой точке.

31.

Экономическая интерпретация задачи, двойственной задаче об использовании ресурсов:

Задача об использовании ресурсов в общем виде.

- прибыль от реализации одной единицы продукции.



,- норма расхода ресурса i-ого вида на производство одной единицы продукции j-ого вида,- количество ресурсов по i -ому виду ресурсов (i=1…n), x1, xn≥0

Двойственная задача: Предположим, что некоторая организация решила закупить ресурсы (S1…Sn) предприятия и необходимо установить оптимальные цены на эти ресурсы. Y1..Ym- цены ресурсов. Р1…Pn – предприятия. Очевидно, что покупающая организация заинтересована в том, чтобы затраты на все ресурсы в количестве были минимальными, т е с точки зрения покупающей организации – целевая функция:

С другой стороны, предприятие, продающее ресурсы заинтересовано в том, чтобы полученная выручка была не меньше той суммы, которую предприятие может получить при переработки ресурсов в готовую продукцию.

- сумма денег, которую получить продающее предприятие, когда оно продаст ресурсы, идущие на производство 1-ой единицы продукции первого вида Р1.

Двойственная задача:

32. Свойства взаимно-двойственных задач:





- сумма денег, которую получить

продающее предприятие, когда оно продаст ресурсы, идущие

на производство

1-ой единицы продукции первого вида Р1.

Двойственная задача:

С итое - прибыль от реализации одной единицы продукции.