ответы к экзамену. 1. Понитие nмерного вектора, основные определения
 Скачать 8.76 Mb.
|
Доказательство (условия совместности системы)НеобходимостьПусть система совместна. Тогда существуют числа  такие, что  . Следовательно, столбец  является линейной комбинацией столбцов  матрицы  . Из того, что ранг матрицы не изменится, если из системы его строк (столбцов) вычеркнуть или приписать строку (столбец), которая является линейной комбинацией других строк (столбцов) следует, что  .ДостаточностьПусть  . Возьмем в матрице какой-нибудь базисный минор. Так как  , то он же и будет базисным минором и матрицы  . Тогда, согласно теореме о базисном миноре, последний столбец матрицы будет линейной комбинацией базисных столбцов, то есть столбцов матрицы . Следовательно, столбец свободных членов системы является линейной комбинацией столбцов матрицы .13. Методы решения систем линейных алгебраических уравнений Метод обратной матрицы В этом разделе мы рассмотрим частный случай системы (1.35), когда число уравнений равно числу неизвестных, т. е. m=n. Система уравнений имеет вид {a11x1+a12x2+...+a1nxn=b1 {a21x1+a22x2+...+a2nxn=b2 {…........................................ {am1x1+am2x2+...+amnxn=bm Квадратная матрица А порядка n этой системы получается из матрицы (1.36) при m= n. В матричной форме система уравнений (1.40) имеет вид (1.38). Пусть матрица системы А является невырожденной, т. е. существует обратная матрица А '. Умножив обе части этого уравнения слева на А ', получаем решение системы (1.40) в матричной форме: (1.41) Х = А^В. Вычисление обратной матрицы по заданной матрице А производится по довольно сложным формулам. В случае, когда порядок п матриц А 1 -1 и A достаточно велик, нахождение обратной матрицы может быть довольно трудоемким процессом. Метод Крамера Другой метод решения системы уравнений (1.40) основан на теореме Крамера. Составим определитель матрицы системы А: Δ=|a11 a12 … a1n| |a21 a22 … a2n| |.........................| |am1 am2 … amn| который называется также определителем системы. Теорема 1.6 (правило Крамера). Пусть А — определитель матрицы системы А, а А, — определитель, полученный из определителя А заменой j-vo столбца столбцом свободных членов В. Тогда, если Д * 0, то система линейных уравнений (1.40) имеет единственное решение, определяемое по формулам x1=Δj/Δ, j=1, 2, …, n. (1.43) Формулы вычисления неизвестных (1.43) носят название формул Крамера. Метод Гаусса Рассмотрим систему уравнений общего вида (1.35). Пусть для определенности a11≠0 (если а11 = 0, то можно переставить на первое место ненулевое слагаемое или начать с другого уравнения). Умножим первое уравнение системы (1.35) на число a21/a11 и вычтем его из второго уравнения этой системы. Затем умножим обе части первого уравнения на число а31/а11 и вычтем его из третьего уравнения и т. д. — т. е. процесс заключается в последовательном вычитании первого уравнения, умножаемого на числа а11/а11, из i-го уравнения (i= 1, 2, 3, ..., п). Таким образом, в результате элементарных преобразований мы получаем эквивалентную систему в которой, начиная со второго уравнения, отсутствуют слагаемые, содержащие неизвестное Хij. {a11x1+a12x2+...+a1nxn=b, {a22x2+a23x3+...+a2nxn=b1 {…........................................ {am2x2+am3x3+...+amnxm. Здесь верхний индекс в скобках означает новые коэффициенты, полученные после первого шага. Для уменьшения громоздкости записи удобнее оперировать с расширенной матрицей системы, отделяя в ней вертикальной чертой столбец свободных членов. Итак, после первого шага, содержащего (m- 1) элементарных преобразований системы, мы переходим от расширенной матрицы (1.39) исходной системы к расширенной матрице AB=(a11 a12 a13 … a1n | b1) (0 a22 a23 … a2n | b2) (…............................|.....) (0 am2 am3 ...amn| bm) Второй шаг заключается в том, что теперь 2-я строка матрицы (1.45) используется для аналогичных элементарных преобразований строк с 3-й по т-ю: эта строка последовательно умножается на число a12/a22 и вычитается из i-й строки (i = 3, 4,..., m). В результате этих (m - 2) элементарных преобразований получаем новую расширенную матрицу, соответствующую новой эквивалентной системе уравнений. Эта матрица имеет вид AB=(a11 a12 a13 … a1n | b1) (0 a22 a23 … a2n | b2) (0 0 a33 … a3n | b3 ) (…............................|.....) (0 0 am3 ...amn| bm) где верхний индекс означает новые коэффициенты. В случае, если элемент а22 = 0, то второе уравнение можно поменять местами с другим уравнением, у которого элемент a12≠ 0. Продолжим этот процесс аналогичным образом (т. е. на третьем шаге преобразуются строки с 4-й по т-ю, на четвертом шаге — строки с 5-й по m-ю и т. д.) до тех нор, пока не дойдем до последней m-строки. После ( г - 1)-го шага процесса последовательного исключения неизвестных мы получим следующую расширенную матрицу: AB=(a11 a12 … a1r a1r+1 … a1n| b1) (0 a22 … a2r a2r+1 … a2n| b2) (…........................................| …..) (0 0 … arr arr+1 … arn| br) (0 0 … 0 0 … 0 | br+1) (…........................................|.......) (0 0 … 0 0 … 0 | bm) Последние (m — г) строк этой матрицы соответствуют уравнениям эквивалентной системы уравнений 0x1+0x2+...+0xn=b1; i=r+1, r+2,...,m. (1.48) Эти уравнения могут появиться, если соответствующие уравнения исходной системы (1.35) представляют собой линейные комбинации других уравнений этой системы, о чем говорилось в предыдущем разделе. Здесь мы не исследовали заранее систему (1.35) на совместность; поэтому, если эта система несовместна, то хотя бы одно из чисел br=1, br=2, …, bm не равно нулю. Таким образом, метод Гаусса позволяет на определенном шаге установить возможную несовместность исходной системы линейных уравнений или выявить и удалить уравнения, являющиеся линейными комбинациями других уравнений системы (1.35), если она совместна. Пусть система (1.35) совместна, тогда все правые части уравнений (1.48) равны нулю, и после удаления нулевых уравнений в эквивалентной системе и нулевых строк в расширенной матрице получаем матрицу специфического ступенчатого вида, ранг которой равен r. Все элементы этой матрицы, стоящие слева или ниже элементов аm равны нулю: AB=(a11 a12 a13 … a1r … a1n| b1) (0 a22 a23 … a2r … a2n| b2) (0 0 a33 … a3r … a3n| b3) (…........................................| …..) (0 0 0 … arr … arn| br) Эта расширенная матрица соответствует системе уравнений ранга г, которая имеет вид {a11x1+ a12x2+ a13x3+ … +a1nxn= b1 {a22x2+a23x3+ … +a2nxn= b2 {a33x3+ … +a3nxn= b3 {…........................................….. {arrxr+...+arn= br (1.50) Система уравнений (1.50) уже полностью подготовлена к нахождению решения, которое осуществляется снизу вверх, т. е. от последнегоуравнения к первому. Переход от системы (1.35) к эквивалентной ее системе (1.50) называется прямым ходом, а нахождение неизвестных из системы (1.50) — обратным ходом метода Гаусса. Укажем дальней- шую последовательность действий. 1. Если ранг системы (1.35) г=n, то система (1.50) имеет вид {a11x1+a12x2+...+a1rxr=b1 {a22x2+...+a2rxr=b2 {….............................. {arrxr=br (1.51) Поднимаясь снизу вверх, последовательно находим (обратный ход метода Гаусса): — из последнего r-уравнения неизвестное хг = br/ar — из ( r - 1)-го уравнения неизвестное хr-х путем подстановки в это уравнение уже найденного неизвестного х^n — из i-го уравнения неизвестное х, при подстановке в него найденных величин хп хг+1, ..., xi + 1, — и так далее до первого уравнения, из которого при подстановке в него уже найденных величин хr, хг+1,, ..., хr+2 находим х1. 2. Ранг системы уравнений (1.50) г < п. В этом случае объявляем неизвестные хг+ь хг+2у •> хп свободными и формируем правые части уравнений (1.50), оставляя в левых частях слагаемые, содержащие базисные переменные х1, х2, ..., хr;. {a11x1+a12x2+...+a1rxr=b1-a1r+1xr+1 - … -a1nxn, {a22x2+...+a2rxr=b2-a2r+1xr+1 - … -a2nxn {…................................................. {arxr=brr+1xr+1 - … - arnxn. Решение этой системы находится обратным ходом метода: теперь базисные неизвестные зависят от свободных неизвестных, которые могут принимать любые значения, а потому система (1.35) имеет бесчисленное множество решений. 14. Решение СЛАУ прямоугольного вида(mxn). Общее решение, частное решение, базисное решение, опорное решение: Общим решением разрешенной системы уравнений называется совокупность выражений разрешенных неизвестных через свободные члены и свободные неизвестные: 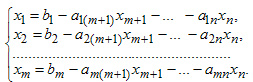 Частным решением системы уравнений называется решение, получающиеся из общего при конкретных значениях свободных переменных и неизвестных. Базисным решением называется частное решение, получающееся из общего при нулевых значениях свободных переменных.
|