ЭЭИС. 1. Понятие электрической цепи и их классификация
 Скачать 2.56 Mb. Скачать 2.56 Mb.
|
|
1. Понятие электрической цепи и их классификация. Электрической (радиотехнической) цепью (ЭЦ) называют любую совокупность электрорадиотехнических устройств, электромагнитное состояние которых допустимо и целесообразно характеризовать с помощью понятий "электрическое напряжение" и "электрический ток". 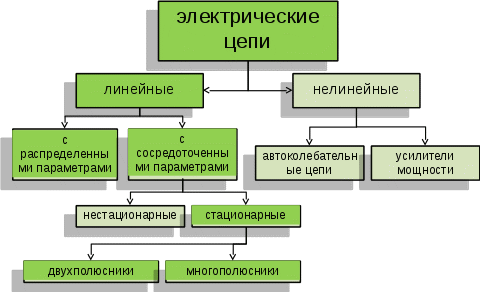 2. Основные топологические понятия электрических цепей. Место соединения зажимов двух и более элементов называется узлом электрорадиоцепи. Ветвь – это часть цепи, которая включена между двумя узлами и взаимодействует (обменивается энергией) с остальной цепью только через эти два узла. Графическое изображение совокупности узлов цепи и соединительных путей между ними, т.е. ветвей цепи, называется графом цепи Путь –последовательность ветвей, соединяющих два узла, при условии, что в этой последовательности нет повторяющихся узлов. Любой замкнутый путь в графе цепи называется контуром. 3. Элементы электрических цепей и виды их соединений. Элементом ЭЦ называется идеализированное устройство, обладающее свойством вносить энергию в электрическую цепь; рассеивать энергию; запасать энергию в виде магнитного или электрического полей. Элементы электрических цепей: а) активные б) пассивные Активные: электрохимические источники тока, электромашинные генераторы; термопары; микрофоны; генераторы Пассивные: элемент резистивного сопротивления; элемент индуктивности; элемент ёмкости; Элемент резистивного сопротивления способен рассеивать энергию или преобразовывать ее в другие виды энергии; Независимым источником напряжения считается такой источник, у которого напряжение на его зажимах не зависит от свойств внешней, подключаемой к нему цепи. 4. Основы расчета резистивных электрических цепей.  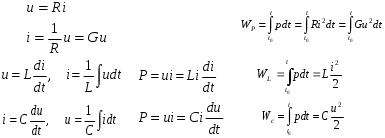 5. Метод узловых напряжений. Метод анализа колебаний в электрических цепях, в котором неизвестными, подлежащими определению, являются узловые напряжения, называется методом узловых напряжений Последовательность решения задач МУН: 1. Выбирается базисный узел (к которому подсоединяется наибольшее число ветвей). Потенциал базисного узла полагают равным нулю. Выбирают направления токов ветвей. Нумеруют узлы. 2. Для определения потенциалов узлов составляют уравнения по 1-му закону Кирхгофа, т.е. N=Nу–1уравнений. В результате решения получают значения узловых напряжений. 3. По найденным узловым напряжениям определяют токи в ветвях и использованием обобщенного закона Ома. 4. Делается проверка с использованием I или II законов Кирхгофа. Правила составления уравнений по методу узловых напряжений: В левой части уравнения записывается всегда со знаком «+» произведение узлового напряжения данного узла на его собственную проводимость. Эта сумма проводимостей всех ветвей, подключенных к данному узлу. Другие слагаемые всегда записываются со знаком «-» и представляют собой произведение узлового напряжения смежного узла на взаимную проводимость между данными и смежными узлами. В правой части уравнения записывается аналогичная сумма токов источников тока, подключенных к выбранному узлу. 1. Если в схеме имеются источники напряжений, то целесообразно заменить их в начале источниками тока. 2. Если в схеме имеется индуктивно связанные катушки индуктивности, то метод узловых напряжений применять нельзя. 3. Если в схеме имеется источник напряжения с внутренним сопротивлением, равным 0, то в качестве базисного узла надо выбирать один из зажимов этого источника. В общем случае в качестве базисного узла надо выбирать тот узел, к которому подключено наибольшее количество источников. 6. Метод контурных токов. Метод анализа колебаний в электрических цепях, в котором неизвестными, подлежащими определению, являются контурные токи, называется методом контурных токов. Последовательность решения задач методом контурных токов: 1.Определяют и нумеруют независимые контуры. Задают направление контурных токов. Контурные токи выбирают так, чтобы по любой ветви проходил хотя бы один контурный ток. 2. Составляют и решают уравнения. Находят контурные токи. При этом общее количество уравнений, составляемых по МКТ, равно числу уравнений, составляемых по II закону Кирхгофа, т.е. N = NB - Ny+1. 3.Токи ветвей определяются алгебраическим суммированием найденных контурных токов протекающих через ветвь. Если в ветви протекает один контурный ток, то истинный ток в ветви принимается равным контурному току. 4. Зная токи ветвей, по закону Ома находят напряжения на элементах. 5. Осуществляют проверку полученных значений токов в ветвях и напряжений на элементах, используя I или II законы Кирхгофа. Правила составления уравнений по методу контурных токов: В левой части уравнения всегда записывается со знаком «+»: 1.произведение контурного тока данного контура на собственное сопротивление данного контура (т.е. сумма всех сопротивлений, входящих в контур). 2. Со знаком «+» или «-» произведение смежного контурного тока на взаимное сопротивление между данным и смежным контуром. При этом знак «+» берется, если контурные токи данного и смежного контурного тока совпадают, а знак «-» - в противном случае (направления контурных токов данного и смежного контуров встречные). В правой части: записывается алгебраическая сумма всех ЭДС, входящих в контур. При этом со знаком «+» берутся эдс, направления токов которых совпадают с направлением контурного тока; со знаком «-» не совпадающие с направлением контурного тока. 7. Определение гармонических напряжений и токов. Гармоническое напряжение, гармонический ток - колебания напряжения и тока, изменяющиеся по закону синуса или косинуса на всем интервале времени. Мгновенные значения гармонических напряжений и токов описываются соотношениями: 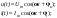 где: Um,Im - амплитуда напряжения и тока; где: Um,Im - амплитуда напряжения и тока;ω– круговая частота; φu , φi - начальная фаза. Амплитуда (Um, Im)представляет собой максимальное значение напряжения или тока за период колебания (единицы измерения [В] или [А]). Период колебания (Т) - наименьший интервал времени, через который процесс повторяется (время одного колебания) (единицы измерения [с]). Частота (f) - число колебаний в единицу времени (в сек.). Размерность частоты: [Гц]=[1/с]. Начальная фаза (φ) - величина угла, определяющего значение гармонического колебания в момент t =0 (единицы измерения [радианы (градусы)]). Функция (ωt + φ) называется мгновенной фазой гармоническогоколебания.Она характеризует степень развития колебательного процесса во времени. Круговая частота (ω=2πf) - изменение мгновенной фазы за единицу времени [рад/с] 8. Символическое изображение гармонических колебаний комплексными числами. Исходные функции называются оригиналами, а соответствующие им новые функции – изображениями или символами. Идея символического изображения гармонических колебаний состоит в замене гармонических функций комплексными числами. Возможность такого изображения гармонических функций заложена в том, что в режиме гармонических колебаний все колебания имеют одну и ту же заранее известную частоту ω, равную частоте внешнего воздействия. 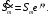   к  омплексной амплитудой или символическим изображением гармонического колебания: её модуль равен амплитуде Sm, а аргумент – начальной фазе φ гармонического колебания. Комплексные амплитуды напряжения и тока имеют вид: омплексной амплитудой или символическим изображением гармонического колебания: её модуль равен амплитуде Sm, а аргумент – начальной фазе φ гармонического колебания. Комплексные амплитуды напряжения и тока имеют вид:9. Законы Ома и Кирхгофа для комплексных амплитуд колебаний. Обобщая соотношения между напряжениями и токами на элементах цепей, можно сделать вывод, что в комплексной форме они подчиняются закону Ома.      - для активного сопротивления; - для активного сопротивления; -  для индуктивности; для индуктивности;  - для емкости. - для емкости.   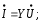 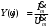 где: Z – комплексное сопротивление элемента цепи (импеданс) где: Z – комплексное сопротивление элемента цепи (импеданс)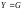 г 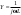 де: Y – комплексная проводимость элемента цепи - для активного сопротивления; де: Y – комплексная проводимость элемента цепи - для активного сопротивления;- для индуктивности; 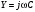 - для емкости. - для емкости.Законы Кирхгофа в комплексной форме 1 закон Кирхгофа: сумма комплексов токов в узле равна нулю. 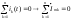 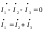  2 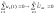  закон Кирхгофа: сумма комплексов напряжений в контуре равна нулю. закон Кирхгофа: сумма комплексов напряжений в контуре равна нулю.  10. Комплексные сопротивления элементов электрических цепей. Двухполюсником называется участок цепи, взаимодействующий с остальными элементами цепи через одну пару зажимов – «два полюса».   полное сопротивление двухполюсника. Представим комплексное сопротивление и комплексную проводимость в алгебраической форме:  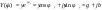 где: r – активная составляющая комплексного сопротивления, x – реактивная составляющая комплексного сопротивления. где: g– активная составляющая комплексной проводимости, b – реактивная составляющая комплексной проводимости. 12. Комплексные передаточные функции электрических цепей. Комплексной передаточной функцией (КПФ) называется отноше- ние комплексной амплитуды реакции к комплексной амплитуде воздействия: 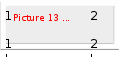 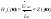 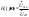 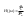 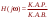 - комплексный коэффициент - комплексное сопротивление . передачи по напряжению. 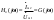 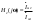 - комплексный коэффициент - комплексная проводимость 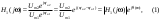 передачи по току. передачи по току.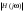 -АЧХ 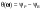 -ФЧХ 11. Анализ установившихся гармонических колебаний в простейших электрических цепях Основная особенность применения законов Ома и Кирхгофа в комплексной форме для анализа электрических цепей символическим методом заключается в том, что вместо мгновенных значений напряжений и токов вводятся комплексные амплитуды, а вместо активных сопротивлений - комплексные сопротивления соответствующих элементов. 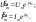 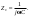 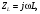 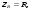 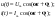 При использовании символического метода анализа интегро-дифференциальные уравнения состояния цепи заменяются алгебраическими уравнениями для комплексных амплитуд напряжений и токов, а коэффициенты этих уравнений являются комплексные сопротивления или комплексные проводимости. ОБЩИЙ ПОРЯДОК РЕШЕНИЯ ЗАДАЧИ АНАЛИЗА СИМВОЛИЧЕСКИМ МЕТОДОМ 1) Определяются комплексные амплитуды воздействий. 2) Рассчитываются комплексные сопротивления элементов. 3) Изображается схема замещения. 4) Рациональным методом определяется комплексная амплитуда реакции. 5) Записываются мгновенные значения реакции. 6) Формулируются выводы. 13. Амплитудно-частотная и фазо-частотная характеристики электрических цепей. А  мплитудно-частотной характеристикой называется частотная зависимость отношение амплитуды гармонической реакции к амплитуде гармонического воздействия. мплитудно-частотной характеристикой называется частотная зависимость отношение амплитуды гармонической реакции к амплитуде гармонического воздействия. Фазо-частотной характеристикой называется частотная зависимость разности начальных фаз реакции и воздействия. АЧХ и ФЧХ нетрудно определить из алгебраической формы представления КЧХ :    -АЧХ -АЧХ-ФЧХ Из определений частотных характеристик следуют важные выводы: 1. Комплексная частотная характеристика содержит в себе амплитудно-частотную и фазочастотную характеристики цепи; 2. Комплексная частотная характеристика цепи численно равна комплексной амплитуде реакции цепи на воздействие, описываемое единичной гармонической функцией x(t)= cos ωt; 3. Частотные характеристики электрической цепи зависят только от параметров самой цепи и не зависят от воздействия. 14. Параметры и частотные характеристики последовательного колебательного контура. Параметры последовательного колебательного контура Первичными параметрами контура являются значения R,L,C. Вторичными параметрами контура являются:  1) частота резонанса: 1) частота резонанса: 2) волновое сопротивление ρ, (сопротивление реактивного элемента (любого) контура при резонансе): 3  ) добротность контура Q. ) добротность контура Q. Добротностью ПсКК (Qпосл.) называется отношение амплитуды напряжения на реактивном элементе к амплитуде ЭДС источника:  Ч 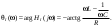 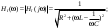 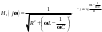 астотные характеристики последовательного колебательного контура астотные характеристики последовательного колебательного контура 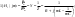 -АЧХ -ФЧХ -АЧХ -ФЧХ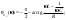 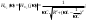 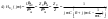 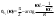     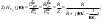 15. Параметры и частотные характеристики параллельного колебательного контура. Параметры параллельного колебательного контура Первичными параметрами контура являются R,L,C. Вторичными параметрами контура являются: 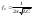 1) частота резонанса: 1) частота резонанса: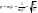 2) волновое сопротивление ρ, (сопротивление реактивного элемента (любого) контура при резонансе): 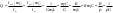 3) добротность контура Q. 3) добротность контура Q. Добротностью ПрКК (Q) называется отношение амплитуды тока на реактивном элементе к амплитуде тока источника: Используя закон Ома в символической форме, для реакции Umполучим: 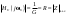 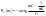 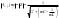 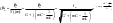 -АЧХ -ФЧХ -Резонанс -АЧХ -ФЧХ -Резонанс16. Операторный метод анализа колебаний в электрических цепях.  Основные положения операторного метода анализа колебаний в электрических цепях Основные положения операторного метода анализа колебаний в электрических цепяхИдея операторного метода анализа колебаний в электрических цепях состоит в том, что уравнения, описывающие процессы в этих цепях при произвольных воздействиях и заданных начальных условиях, составляются для L-изображений напряжений и токов, а не для мгновенных значений. В результате из их решения находится изображение искомой реакции. После этого выполняется переход от изображения к оригиналу. В основе составления уравнений для L-изображений колебаний лежат законы Ома и Кирхгофа, записанные в операторной форме. Если u(t)и i(t) функции напряжения и тока, то в результате применения к ним преобразования Лапласа получим преобразованные по Лапласу:  Прямое преобразованные по Лапласу Обратное преобразованные по Лапласу   Где p=+j - оператор преобразования Где p=+j - оператор преобразования Применим преобразование Лапласа к соотношениям, связывающим напряжения и токи для пассивных элементов электрических цепей: Применим преобразование Лапласа к соотношениям, связывающим напряжения и токи для пассивных элементов электрических цепей:  для элемента индуктивности: для элемента индуктивности: для элемента сопротивления: для элемента сопротивления: 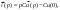 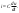 для элемента емкости: О 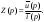 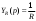 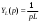 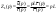 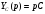 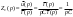  ператорным сопротивлением двухполюсниканазывается отношение преобразованного по Лапласу напряжения к преобразованному по Лапласу току при нулевых начальных условиях: ператорным сопротивлением двухполюсниканазывается отношение преобразованного по Лапласу напряжения к преобразованному по Лапласу току при нулевых начальных условиях:17.Типовые воздействия на электрические цепи.  1. Ступенчатымвоздействием напряжения (тока) называют воздействие, которое описывается функцией: 1. Ступенчатымвоздействием напряжения (тока) называют воздействие, которое описывается функцией: 2. Импульснымвоздействием на электрическую цепь называется воздействие, которое описывается функцией:    - площадь воздействия (импульса); - единичная импульсная функция (дельта-функция, функция Дирака). - площадь воздействия (импульса); - единичная импульсная функция (дельта-функция, функция Дирака).3. Воздействие в виде отрезка гармонического колебания определяется функцией вида:    Законы коммутации 1) 2) 1-й закон - ток в индуктивности скачком измениться не может. 2-й закон напряжение на емкости скачком измениться не может. 18. Переходные процессы в цепях с одним реактивным элементом. Колебания в электрической цепи, происходящие после прекращения воздействия за счёт энергии, накопленной в реактивных элементах, называются свободными колебаниями, а состояние цепи при этом называется режимом свободных колебаний. Неустановившиеся колебания, которые наблюдаются в цепи при переходе от одного установившегося состояния к другому, обычно называются переходными. П   оскольку в данном случае рассматривается переходной процесс при нулевых начальных условиях, то начальные значения всех реакций легко определить как: оскольку в данном случае рассматривается переходной процесс при нулевых начальных условиях, то начальные значения всех реакций легко определить как:В  установившемся режиме, т.е. при t→∞ емкостной элемент оказывается эквивалентным "разорванной" цепи. Установившиеся значения реакций будут следующими: установившемся режиме, т.е. при t→∞ емкостной элемент оказывается эквивалентным "разорванной" цепи. Установившиеся значения реакций будут следующими:Для нахождения знаков изменения тока i(t) и напряжения uC(t)иuR(t)воспользуемся операторным методом.   1. Изображение ступенчатоговоздействия равно E/p, операторное сопротивление цепи: 1. Изображение ступенчатоговоздействия равно E/p, операторное сопротивление цепи: 2. По закону Ома в операторной форме находим изображение тока: 2. По закону Ома в операторной форме находим изображение тока:  3. Изображение напряжения на элементах цепи равны: 3. Изображение напряжения на элементах цепи равны:П  ользуясь таблицей соответствий (строка 5 и 6), получим: ользуясь таблицей соответствий (строка 5 и 6), получим:   19. Переходная и импульсная характеристики. П  ереходной характеристикой цепи h(t) называется отношение реакции цепи на ступенчатое воздействие y(t) к величине этого воздействия A при нулевых условиях в цепи, т.е. ереходной характеристикой цепи h(t) называется отношение реакции цепи на ступенчатое воздействие y(t) к величине этого воздействия A при нулевых условиях в цепи, т.е.Другими словами переходная характеристика численно равна реакции цепи на единичное ступенчатое воздействие при нулевых начальных условиях. Очевидно, что если h(t) известна, то реакция цепи на ступенчатое воздействие может быть определена как  Импульсной характеристикой цепи g(t) называется отношение реакции цепи на импульсное воздействие к площади этого воздействия при нулевых условиях, т.е. где y(t) – реакция цепи на импульсное воздействиеSи . Импульсной характеристикой цепи g(t) называется отношение реакции цепи на импульсное воздействие к площади этого воздействия при нулевых условиях, т.е. где y(t) – реакция цепи на импульсное воздействиеSи . Можно также считать, что импульсная характеристика численно равна реакции цепи на единичное импульсное воздействие. Временные характеристики удобно вычислять на основе операторного метода, используя понятие операторной передаточной функции. 20. Операторные передаточные функции электрических цепей О  ператорная передаточная функция цепи H(p)называетсяотношение L-изображения реакции к L-изображению воздействия при нулевых начальных условиях. ператорная передаточная функция цепи H(p)называетсяотношение L-изображения реакции к L-изображению воздействия при нулевых начальных условиях.Допустим, что к цепи приложено ступенчатое воздействие    ступенчатое воздействие. Тогда операторная передаточная функция будет иметь вид:  Если же на цепь подается импульсное воздействие Если же на цепь подается импульсное воздействие Э  то выражение совпадает с функцией изображения импульсной характеристики цепи. Следовательно, то выражение совпадает с функцией изображения импульсной характеристики цепи. Следовательно, 21. Связь между временными и частотными характеристиками цепи Д  ля данной цепи определить операторную передаточную функцию и найти выражения для ее частотных характеристик ля данной цепи определить операторную передаточную функцию и найти выражения для ее частотных характеристикИзображение реакции определим из системы узловых уравнений, составленных для L-изображений узловых напряжений       где для упрощения записи введено обозначение : Отсюда где для упрощения записи введено обозначение : ОтсюдаДля нахождения комплексной передаточной функции положим в последнем выражении p=j/ῳ Тогда  АЧХ определяется модулем полученной функции, а ФЧХ находим как аргумент АЧХ определяется модулем полученной функции, а ФЧХ находим как аргумент    22. Классификация сигналов. Сигнал – это физический процесс, отображающий передаваемое сообщение и способный распространятся с определенной скоростью от источника к получателю сообщения (звуковые и электромагнитные волны, электрический ток). Электрический сигнал – это значение или изменение значения во времени величины электрического тока или напряжения.          23. Основные характеристики сигналов.    24. Преобразование типа сигналов.       25. Спектр периодической последовательности прямоугольных видеоимпульсов.       26. Общие сведения о модулированных сигналах.   27. Временное и спектральное представление АМ сигналов.       28. Временное представление сигналов с частотной модуляцией.          |
